mTopKRP:遥感图像鲁棒特征匹配的多尺度局部性和秩保持
mTopKRP:遥感图像鲁棒特征匹配的多尺度局部性和秩保持

摘要:
作为遥感和摄影测量的许多应用中的一项基本而重要的任务,特征匹配试图寻找从同一对象或场景的图像对中提取的两个特征集之间的对应关系。本文的重点是从一组假定的特征对应关系中消除不匹配,这些特征对应关系是根据现有精心设计的特征描述符的相似性构建的。考虑到潜在真实对应关系的稳定局部拓扑关系,我们提出了一种简单而有效的方法,称为多尺度 Top K Rank Preservation (mTopKRP),用于稳健的特征匹配。为此,我们首先搜索每个特征点的 K 近邻,并相应地生成一个排序列表。然后我们设计了一个基于加权斯皮尔曼足迹距离的度量来描述两个排名列表的相似性,专门用于匹配问题。我们建立了一个数学优化模型并推导出其封闭形式的解决方案,使我们的方法能够在线性时间复杂度中建立可靠的对应关系,只需要几十毫秒来处理超过 1000 个假定的匹配。我们还引入了一种用于邻域构建的多尺度策略,这增加了我们方法的鲁棒性,并且可以处理不同类型的退化,即使图像对遭受大尺度变化、旋转、非刚性变形或大量不匹配时也是如此。对几个具有代表性的遥感图像数据集的广泛实验证明了我们的方法优于现有技术。
关键词:特征匹配、局部结构、多尺度、非刚性、排名表。
1. 引言
特征匹配旨在从同一对象或场景的两个图像中建立可靠的特征点(例如像素坐标)对应关系,是许多基于视觉的任务的基本和关键问题,特别是对于遥感和摄影测量的应用,包括图像配准和融合[1]-[3]、全景图像拼接[4]、[5]、3-D重建[6]、[7]、目标识别和跟踪[8]、[9]。这些基于匹配的任务通常是基于鲁棒和有效的特征匹配方法来完成的,以获得尽可能多的正确匹配,同时将不匹配保持在最低限度。
特征匹配是一个组合性质的问题,在非帕累托准则复杂优化中造成了很高的计算复杂度。具体来说,将 N 个点匹配到另一个 N 个点可能会导致总共 N!排列[10]。为了解决这个问题,许多现有方法的共同思想是以两阶段的方式解决特征匹配问题,首先基于与不同特征点相关联的局部补丁描述符的相似性构造一组假定匹配,例如局部像素的梯度、强度值或提取的不同且稳定的极值点的其他描述[11]-[13]。然而,除了一些正确的对应关系(即内点)之外,由于局部描述符的模糊性,假设集中还有大量的错误匹配(即异常点),特别是当图像对遭受低- 质量、遮挡或重复模式。因此,在下一步中,使用附加约束从构建的假定匹配集中过滤掉不匹配是至关重要的。
许多现有的不匹配去除方法通常基于几何约束,将假定的匹配集视为通过满足预定义的几何变换模型[14]从输入到输出的映射。然而,由于地势变化、成像视点变化、在低空或由鱼眼(FE)相机捕获,遥感图像往往会出现局部失真,从而导致复杂的空间关系。因此,转换模型可以针对不同的数据而变化,并且通常事先是未知的,特别是如果它是非刚性的。在这种情况下,使用预定义的几何模型可能会导致较差的匹配精度。现有方法的另一个障碍是复杂的非刚性变换模型导致计算复杂度大,不适用于处理大规模或实时任务,例如基于无人机 (UAV) 的任务,包括 3-D 陆地表面重建、大面积图像拼接、运动物体检测和跟踪[4]、[6]、[15]。
为了解决上述挑战,我们提出了一种基于两个局部结构之间相似性的鲁棒遥感图像匹配方法,两个局部结构分别由两个匹配特征点的K最近邻(K-NN)组成。特别是遥感图像中相邻特征点之间的关系通常是稳定的,即使图像经过尺度变化、旋转或非刚性变换[1],也只会发生微小的变化。基于这一观察,我们开发了一种测量方法来描述两个局部结构的相似性,并相应地建立一个数学优化模型来识别错误匹配。我们的模型是通用的,不需要预定义的转换模型,并且对于封闭形式的解决方案也非常有效。这项工作是我们之前在 [16] 和 [17] 中工作的扩展。与我们之前的工作相比,在本文中,我们重新定义了基于多尺度邻域的排名列表距离测量,以更严格和更普遍地保留局部拓扑结构,这使得我们的方法对异常值和不同类型的退化更加鲁棒。
总之,我们的主要贡献是双重的。一方面,提出了一种简单而有效的方法来解决鲁棒特征匹配问题。与现有方法相比,我们的方法仅通过保留潜在内点的局部拓扑结构来消除不匹配,这与具有特定参数或非参数模型的任何预定义全局图像变换无关,因此,它对不同类型的模型更加通用和鲁棒的图像变换。另一方面,我们为失配消除问题引入了一个通用的数学优化模型,并推导出了它的闭式解。基于该模型,任何描述异常值和异常值之间潜在差异的标准都可以集成到我们的公式中。此外,封闭形式的解决方案使我们能够在线性时间复杂度中建立可靠的对应关系,处理超过 1000 个假定匹配只需要几十毫秒。
本文的其余部分安排如下。第二节介绍了背景材料和相关工作。在第三节中,我们详细介绍了我们的多尺度 Top K 排名保留 (mTopKRP) 算法,包括 K 排名相似度的测量、一般目标函数及其封闭形式的解决方案。第四节提供了我们方法的定性和定量评估,并与不同类型的遥感图像数据集上的几种最先进的方法进行了比较。最后,第五节总结了一些结论性意见。
2. 相关工作
一般来说,特征匹配问题可以通过两阶段的方式来解决。在第一阶段,从每幅图像中提取显着特征,即控制点及其描述符,并利用描述符的相似性约束构造一组假定的点对应关系。解决这一阶段的经典方法包括尺度不变特征变换 (SIFT) [11]、加速鲁棒特征 (SURF) [12] 以及定向 FAST 和旋转简要 (ORB) [13],这些方法已被证明是有效的并且有效。 SIFT在高斯尺度空间中检测特征点,并使用梯度直方图形成描述子,已知其具有尺度、视点、旋转和光照不变性。 SURF 通过使用 Hessian 矩阵进行准确的特征检测和积分图像策略来提高 SIFT 的效率。具体来说,李等人。 [18] 改进了 SIFT 的描述符,以克服远程图像对之间梯度强度和方向的差异。相比之下,ORB 对特征检测和描述采用了不同的方案。它通过使用 FAST 检测器 [19] 和简要描述符 [20] 实现了更高的速度,同时牺牲了尺度不变性。然而,由于描述符匹配的模糊性,这个假定的对应集通常被大量异常值污染。因此,第二阶段希望通过全局几何约束去除异常值,从而获得准确的特征匹配结果。在本文中,我们假设假定的对应关系已经构建,然后我们关注错配消除问题。文献中已经提出了各种解决这个问题的方法,在这里,我们对它们进行简要回顾。
错配去除方法大致可分为两类,即重采样和非参数拟合方法。随机样本一致性(RANSAC)[14]是文献中最具代表性的方法之一,它试图通过随机重采样找到符合预定义参数模型的最大无异常对应集。受 RANSAC 的启发,最大似然估计样本共识 (MLESAC) [21] 和渐进样本共识 (PROSAC) [22] 被提议作为有效的变体。尽管重采样方法在特征匹配问题上取得了巨大成功,但它们也存在一些局限性。当图像场景的运动是非刚性的,不能用参数模型来表征时,这些方法将无效。为此,引入了非参数拟合方法,例如向量场一致性(VFC)[23]、识别对应函数(ICF)[24]和鲁棒L2估计器[25]。通过使用 M 估计器或非线性回归技术,这些方法能够对非刚性运动场进行鲁棒拟合。与恢复的运动一致的对应被识别为内点。但是,在存在大量异常值的情况下,它们的性能将不可避免地下降。
特征匹配的另一种策略是直接建立两个特征集之间的对应关系。这些方法还涉及两类。迭代最近点(ICP)[26]和相干点漂移(CPD)[27]是第一类的代表,旨在估计两个特征集之间的转换模型。特别是,对于预定义的参数或非参数模型,这些方法在两个更新过程之间迭代,即对应关系建立和变换估计,直到收敛。然后可以同时确定特征对应和变换模型。基于高斯混合模型的配准(GMMREG)[28] 为点集配准提供了一个通用框架,旨在最小化两个点集的两个高斯混合分布之间的统计差异测量。第二类称为图匹配方法[29]、[30]。光谱匹配(SM)[31]、具有仿射约束的SM(SMAC)[32]和图位移(GS)[33]是这一类的代表。通常,这些方法不依赖于特定的转换模型。相反,他们将特征匹配问题表述为整数二次规划 (IQP) 问题,该问题强制保留两个特征集之间的几何结构。对应关系由它的最优解决定。然而,这两类方法都抛弃了特征(例如描述符)的局部图像信息,而仅利用了空间信息。因此,它们的性能可能会有所下降,同时时间成本也很高。
在遥感界,特征匹配文献还包括多种方法[34]-[37]。例如,提出了局部线性变换 (LLT) [1] 来解决失配消除问题,它同时适应参数和非参数变换模型,并开发了一种新的局部结构约束。温等人。 [38]引入了一个统一的特征匹配标准,它结合了空间一致性和特征相似性。此外,提出了一种基于图匹配的方法,即受限空间顺序约束(RSOC)[39],以实现基于空间顺序约束的精确点匹配。在最近的过去,周等人。 [40] 使用具有全局和局部正则化项的概率方法来区分真假对应。李等人。 [5] 提出使用支持线投票来过滤不匹配和仿射不变比率,以随后细化匹配结果,并且能够发现比初始匹配更正确的匹配。
最近,提出了几种新方法来解决特征匹配问题,通过使用分段平滑约束和局部结构一致性,例如 LPM [16]、[41]、[42]、基于一致性的决策边界 [7]、基于网格的运动统计[43]和深度学习方法[44],它们在准确性和效率方面都取得了可喜的表现。具体来说,LPM 的关键观察是即使在严重变形的情况下,局部拓扑元素通常在一定程度上得到了很好的保留。为了实现尺度和旋转不变,LPM 考虑了特征点的空间邻域关系,并开发了一种鲁棒且令人惊讶的有效错配去除方法。
尽管我们之前开发的 LPM [16] 和 TopKRP [17] 方法保留了来自两个图像的两个假定匹配的特征点的局部拓扑结构,但它们的区别在于两个特征点之间的拓扑相似性度量的定义。具体来说,LPM 仅通过计算 K-NN 的交集来定义特征点之间的局部结构相似性。显然,LPM 忽略了相邻元素之间的差异(即特定的位置关系),不能利用真正的拓扑结构。换句话说,LPM 中的约束不足以保持局部结构,例如,如图 1 所示的前两个示例,其中 LPM 在这两种情况下产生的成本均为 0,而假定这两个图像对中的 match (x, y) 分别是正确的和不正确的。相比之下,在TopKRP [17]中,我们通过将假定的匹配特征点从特征空间转换到排序列表空间,提出了更严格的局部结构保存测量标准,然后测量两个特征点的拓扑结构相似度通过比较他们的排名列表,可以更准确地识别图 1 中前两个示例的异常值和异常值。
3. 方法
为了在两幅遥感图像之间建立可靠的特征对应关系,我们首先使用 SIFT 算法 [11] 构建一组假定匹配,然后匹配任务归结为从给定的假定集中去除错误匹配。因此,在下文中,我们将重点关注基于 K-NN 排序相似度的失配去除,以保留局部拓扑结构。
3.1 Top K 秩相似度测量
为了衡量局部元素的排序相似度,我们首先确定每个特征点的 K-NN。对于每个假定的匹配 (x, y),我们可以获得两个特征点 x 和 y 的排名列表,分别表示为 σ(x) 和 σ(y)。两个排名列表之间的差异可以基于加权的 Spearman 脚尺距离 [45] 来定义。我们将top K rank差异表示为,如下
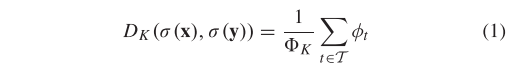
其中,且,是两个完整排名列表和之间的加权斯皮尔曼足迹测量值,用于通过下式将归一化到[0,1]:
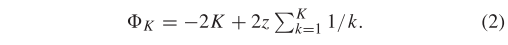
在公式(1)中,项目 t 对的排名距离贡献为:
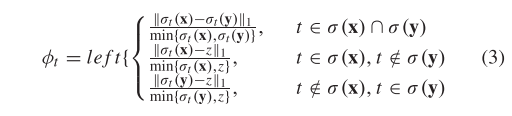
其中,和是元素 t 分别在列表和中的排名,定义基于 :
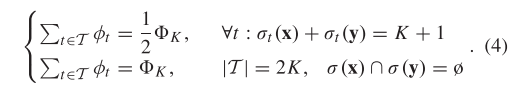
因此,的形式可以写成:
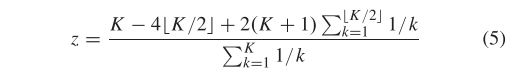
其中运算符将元素四舍五入为不大于该元素的最接近的整数。
接下来,我们证明≥ K,因此当≤ K 时,我们可以将 (3) 中的转换为
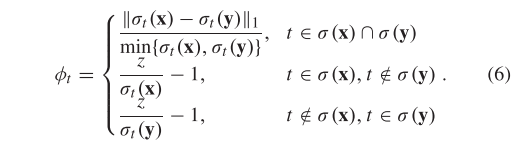
证明:
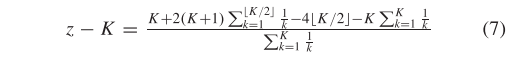
让 公式(7) 的分子表示为。当K = 1时,我们可以得到 = 0。当K≥2且K为偶数时,我们设置K = 2N,N为正整数,并得到
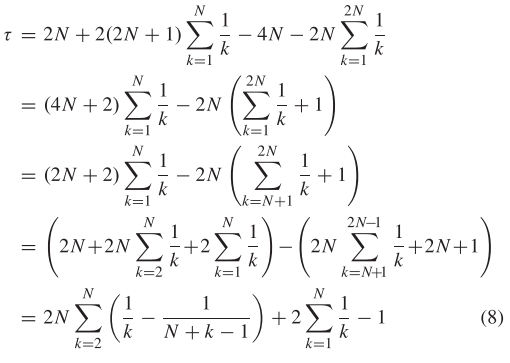
其中,N ≥ 1,因此,我们有 并且。因此,> 0 成立。同理,当K为奇数时,设K=2N+1,也可以得到> 0 。因此,对于任何正整数 K,≥ K 成立。
我们可以从公式 (6) 中对的定义发现,即使当项目 时,也与其在排名列表中的位置或成反比。也就是说,当项目 t 是离对象(即 x 或 y)很近的离群值时,例如图 1 所示的第三个示例,错误匹配 (N, N‘ ) 靠近对象的前面y 的相邻排序列表(例如,),因此项目 N 贡献的成本在排序列表距离测量中占主导地位,即使对象匹配 (x, y) 正确,也可能返回较大的。例如,在图 1 中,公式(6)计算的排序列表距离在右侧图像对中为 0.4595,而对于中间情况的错误匹配,公式(6)计算的距离为 0.3452,这导致误判这两种情况。因此,如果我们在特征匹配任务中直接使用加权的 Spearman 足迹测量,排名列表相似度测量 DK 对异常值很敏感。

图1. 在我们的方法中局部结构排名列表相似性测量的说明。上面展示了三个例子来判断假定的匹配 (x, y) 是否正确。我们从假定的点集中搜索特征点 x 和 y 的 K-NN(K = 4)。我们可以得到这三个例子的 x 和 y 的相邻排序列表,分别是$ {σ(x) = (A, B,C, D), σ(y) = (A’ , B’ , C’ , D’ )}$, 和 。将 (A, A’ ) 这样的匹配点视为同一个项目,我们可以通过局部保持匹配 (LPM) [16]、TopKRP [17] 和本文中改进的 TopKRP(即, mTopKRP),我们相应地将它们表示为。成本分别为 [0, 0, 0](左,真匹配)、[0, 0.3452, 0.3452](中,假匹配)和 [0.25, 0.4595, 0.25](右,真匹配)。假定的匹配用实线表示,其中蓝色和绿色线表示真匹配,红线表示假匹配。虚线圆圈表示以物点 x 或 y 为中心的欧几里得距离范围。
实际上,K-NN排序列表可能是在存在大量不匹配或异常值的情况下构建的,这在特征匹配中经常发生,并且异常值等概率地位于排序列表中的任何位置。为了解决这个问题,我们将计算的标准重新定义为
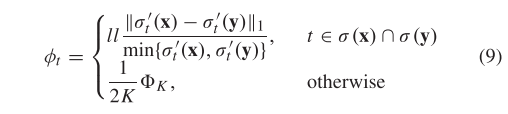
其中,和分别是新列表和中元素 t 的重新排序,仅基于公共元素,例如,在图 1右侧示例中,和。这样,新的邻域秩距离测量标准对异常值的鲁棒性更强,图1这三个例子中的DK分别为0、0.3452和0.25,可以更准确地区分异常值和异常值。
3.2 问题表述
给定一对遥感图像 I 和 I ’,假设我们从上面的图像对中提取出一组 N 个假定匹配 ,其中对应的特征点 xi 和 yi 分别为I 和 I '中的像素坐标。表示未知的内点集。为了保留特征点的局部结构,最优解是
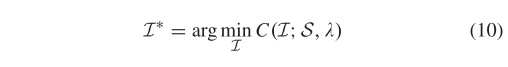
成本函数 C 定义为:
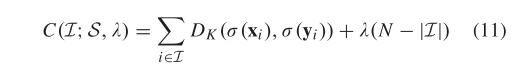
其中和分别表示 xi 和 yi 的前 K 个排序列表,衡量的是 xi 和 yi 的前 K 个排序列表的差异,并且|·|表示集合的基数。在这个成本函数中,第一项惩罚任何不保留局部邻域排名相似性的匹配,第二项用于阻止异常值,正参数控制这两项之间的权衡。理想情况下,最优解应该实现零惩罚,即 C 的第一项应该为零。也就是说,它试图获得最大的内点数并保持成本值最小。
我们引入一个 N × 1 二元向量 p 来关联假定匹配集,其中表示第 i 个假定匹配是否正确。因此,(11)中的成本函数可以写成
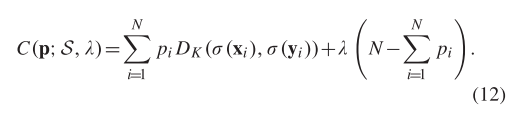
3.2.1 多尺度成本
在上面的公式中,我们为每个特征点构建了 K-NN 以获得其 top K 排序列表,并测量了每个假定匹配与 公式(1) 中的 的排序相似度。然而,K 的最佳值可能会随着不同的图像数据而变化,因为假定集合中异常值的分布和比例会随着图像域的变化而变化。在这种情况下,不适合通过固定 K 的值来解决一般的特征匹配任务。为了解决这个问题,我们开发了一种多尺度策略,该策略测量局部 K 邻域的排序相似度并计算不同尺度下的成本函数的K。因此,我们定义了一组不同的K,其中,第i个假定匹配相对于个最近邻域的排序列表相似度可以表示为。因此,关于(12)的多尺度成本函数可以写成
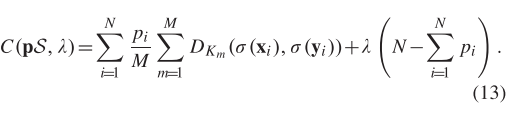
我们通过合并与相关的术语来重组它的形式,得到
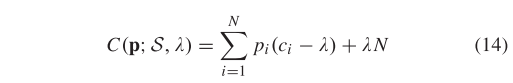
其中:
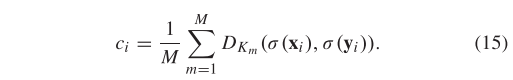
3.3 求解
给定一个假定的匹配集,一旦构建了所有特征点的 K-NN,就可以预先计算的所有成本值。因此,为了确定 公式(14) 中的值,我们可以很容易地观察到,任何成本小于参数的假定匹配都会导致负项并降低目标成本函数,因此我们更愿意将为 1,反之亦然。也就是说,式(14)中代价函数最小的p的最优解可以简单地由以下准则确定:
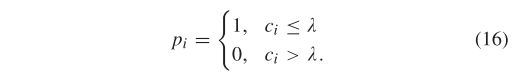
在这种情况下,最优内点集可以由下式确定
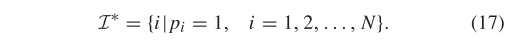
显然,从式(16)中我们可以看出,参数用于判断假定匹配的正确性。然而,局部邻域的排名表是基于整个假定集构建的,通常包含大量异常值,这可能导致对排序列表相似度,最优情况下,如果排序列表仅基于内点集构建,则更可取,这样我们就可以根据和参数正确区分内点和异常点。然而,内点集是我们在匹配任务中需要解决的,无法提前知道。为了解决这个难题,我们利用迭代策略通过在每次迭代中寻找一个近似来确定最优 I,并将其用于邻域构建。
为了验证新的测量标准和迭代策略的效果如何,我们随机选择了总共 30 个具有不同类型变换的遥感图像对,包括刚性、旋转、尺度变化、非刚性变形(如有限元图像)等。SIFT 在整个测试数据上获得的推定匹配的平均初始内点数和内点百分比分别为 1148.2% 和 56.28%。此外,F-score用于评估匹配性能,定义为,其中Precision定义为识别出的正确匹配数与保留匹配的比值数,召回率定义为识别出的正确匹配数与推定集中包含的正确匹配数之比。图 2 总结了关于不同参数 λ 值的 F 分数曲线,其中我们报告了 LPM [16]、TopKRP [17] 和 mTopKRP 的结果。显然,我们的 mTopKRP 极大地提升了匹配性能。在适当的 λ 值(例如 0.8)下,我们获得了 96.48% 的最佳平均 F 分数(AF),其中平均精度(AP)和召回率分别约为 94.76% 和 98.41%。
甚至 K-NN 排名列表也是基于整个假定集构建的,其中涉及相当多的错误匹配,top K rank 保留策略可以很好地工作,并生成一个对应集,可以过滤掉大部分异常值,同时保留大部分异常值。因此,生成的对应集可以很好地逼近真实的内点集,我们将其表示为。为了进一步提高性能,我们随后使用为中的每个假定匹配构建 K-NN 排序列表,并以迭代方式求解最优,即可以根据排序生成第 j 个内点集用第 ( j − 1) 个内部集合构造的列表,可以写为
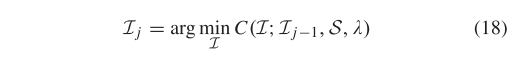
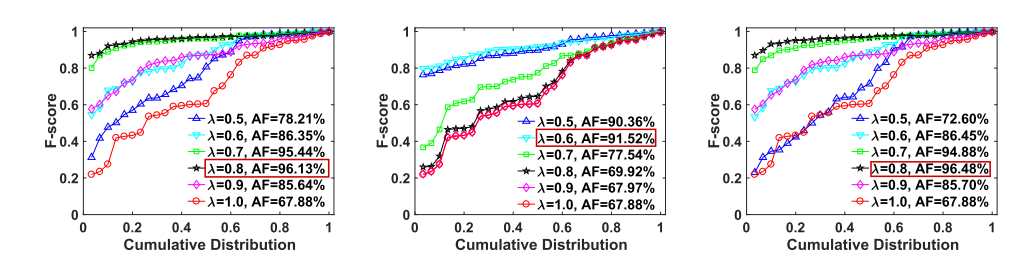
图2. 使用整个特征集在 30 个遥感图像对上构建局部相邻结构的累积分布的 F-score。推定匹配的平均内点数和平均内点率分别为 1148.2% 和 56.28%。 (左)LPM [16] 的结果,我们通过将成本除以 2K 来标准化成本,例如,K = 15。(中)TopKRP [17] 的结果,K = 15。(右)使用新的 mTopKRP 的结果相似性度量标准和多尺度邻域表示,例如,K = [13, 15, 17]。曲线上坐标为 (x, y) 的点表示有 (100 * x)% 的图像对,其 F-score 不超过 y。最佳平均 F 分数及其阈值 λ 在图例中用红色框标记。
其中 j = 1, 2, … , 最大迭代, , 最优内点集可以近似为。图 3 通过使用和构建相邻结构,报告了 (15) 中成本 ci 的分布。显然,我们可以从结果中看到,通过使用精炼集进行邻域构建,内点和异常点之间的边距明显扩大。在参数 λ = 0.35 的情况下,30 个测试图像对的 AP、召回和 F 分数可以从(94.76%、98.41%、96.48%)大幅提高到(98.42%、99.27%、98.83%)。随着迭代的进行,收敛后的AP、召回率和F-score可以进一步提高到(98.70%、99.42%、99.05%)。在本文中,考虑到时间复杂度,我们设置 Max Iter = 3,该值效果很好,可以在遥感图像上产生令人满意的匹配性能。
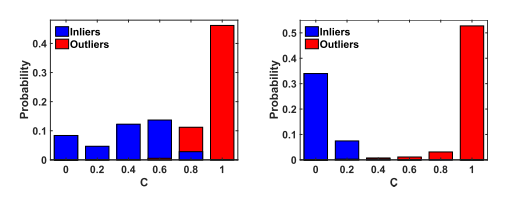
图3. 在 (15) 中的成本 ci 的分布通过使用整个特征集和使用 构建相邻结构。
由于我们的方法旨在保持多尺度 KNN 下前 K 个排名列表的相似性,我们将其命名为 mTopKRP 并在算法 1 中总结整个过程。

3.4 计算复杂度
为了使用KDtree为假定集中的所有特征点构建基于 K-NN 的排名列表,时间复杂度为。因此,算法 1 中第 3 行的时间成本接近于$ O((K_M + N) \log {N}){c_i}{i=1}N$的最少和最多时间成本分别为$O(\sum_{m=1}MK_mN)O(\sum{m=1}^M2K_mN)\mathcal{I}O((K_M+N)\log{N}+(1+2\sum_{m=1}^MK_m)N)O(K_MN)\sum_{m=1}^MK_m\ll N$和我们的算法可以在几次迭代中收敛。也就是说,我们的 mTopKRP 的时间和空间复杂度可以简单地分别写为 O(N log N) 和 O(N)。这对于解决实时或大规模任务非常重要,尤其是在匹配高分辨率遥感图像的情况下。
3.5 实现细节
我们的方法中有三个参数:K、λ 和 Max Iter。参数 K 确定用于多尺度 K-NN 排名列表构建的最近邻域的数量。为了寻求 K 的最佳值,我们在图 2 所示的 30 个遥感图像对上测试了不同的设置,并在表 I 中报告了 AF 和运行时间。从结果中,我们看到 F 分数随着 K 的增加而增加,而运行时间也同时增加。为了在准确性和效率之间取得平衡,我们将 K =[13, 15, 17] 设置为其默认设置。参数 λ 控制判断假定匹配正确性的阈值。参数 Max Iter 表示我们方法中的最大迭代次数。显然,较小的 λ 值会提高精度,同时降低召回率,反之亦然。较大的 Max Iter 值会稍微提高性能,但需要更多的时间成本。在我们的评估中,基于上述实验和分析,我们将这些参数的默认值分别设置为 Max Iter = 3, K =[13, 15, 17], λ = 0.8, 0.35, 0.35 在三个迭代中。
4. 实验结果
在本节中,我们测试了我们提出的方法在不同类型的遥感数据集上的性能,并将其与其他特征匹配方法进行了比较。特别是选择刚性和非刚性遥感图像数据集进行评估,它们具有不同的成像场景。选择了六种最先进的方法进行比较,即 RANSAC [14]、ICF [24]、GS [33]、LLT [1] 和 LPM [16]。这些参数是根据原始论文设置的,并在我们的实验中固定。对于 LLT,我们为每个数据集选择自适应模型。开源 VLFeat 工具箱 [47] 用于 SIFT 检测器和描述符以及使用 K-D 树进行 K-NN 搜索。实验在具有 3.4 GHz Intel Core CPU、8 GB 内存和 MATLAB R2016b 代码的台式机上进行。
4.1 数据集
为了评估我们方法的性能,我们使用如下五个遥感图像数据集。
1)UAV:数据集由35对彩色图像组成,分辨率为600×337,由无人机在一片农田上捕获。这些图像的精确特征匹配在自动作物监测领域尤其需要。通常,由于成像条件不稳定,图像会出现投影失真。
2)SAR:数据集包含 34 对被强噪声破坏的图像对。对于每个图像对,这两个图像分别由卫星和无人机上的合成孔径雷达 (SAR) 分别获得。此类图像对的特征匹配在定位和导航问题中至关重要,其中需要无人机图像匹配相应的存储卫星图像以准确估计当前位置。在大多数情况下,图像对可以用相似性或刚性变换来建模。
3)PAN:数据集由帧相机在不同时间拍摄的 31 对全色 (PAN) 航拍照片组成。这些图像对中经常存在视点变化,从而导致仿射或投影失真。这些图像的特征匹配通常出现在变化检测中。图像有 561 × 518 和 600 × 700 两种尺寸。
4)CIAP:数据集由 40 对彩色红外航空照片(CIAP)组成,大小为 700×700。我们注意到这些图像已经过正射校正,因此变换模型只是刚性的。但是,重叠区域非常小。这些图像的特征匹配在图像拼接问题中很重要。
5)FE:该数据集由 FE 相机从四个场景中捕获的 30 对图像组成 [48]。大多数图像对都受到视点变化的影响,并且还涉及严重的非刚性变形。这些图像用于非参数图像匹配评估。
为了建立ground truth,即确定真正的对应集,我们在进行任何实验之前都做了一个基准,以确保客观性;具体来说,每个图像对中的每个假定对应关系都是手动检查的。
4.2 定性结果
为了证明我们提出的特征匹配方法的有效性,我们首先在图 4 中给出了一些典型图像对的结果。从上到下,五行代表上述五个数据集,即 UAV、SAR、PAN、CIAP , 和 FE,每个都包含两个示例。对于每个示例,左图显示图像对的直观结果,右图显示对应的运动场。对于可见性,左图中仅显示了 100 个随机选择的真阳性、假阴性和假阳性对应关系。右侧运动场显示所有对应的结果,用箭头表示。
由于各种原因,所选图像对对特征匹配任务具有挑战性。具体来说,第一行和第三行遭受投影失真,第二行遭受严重噪声,第四行遭受小重叠区域,最后一行遭受非刚性变形。如前所述,采用 SIFT 算法提取特征,并与许多异常值一起构建大量对应关系。十对图像的初始对应数分别为574、852、539、1084、504、628、305、388、503和644,内点率为42.49%、41.40%、36.05%、42.99%、26.88 %、27.26%、13.28%、15.76%、50.30% 和 15.45%。通过使用我们提出的方法来过滤不匹配,我们可以获得准确率、召回率和 F-score 统计数据,分别为 (99.65%, 99.30%, 0.9948), (99.81%, 99.63%, 0.9972), (99.36%, 99.82% , 0.9959), (99.18%, 99.65%, 0.9941), (99.60%, 100.0%, 0.9980), (100.0%, 99.84%, 0.9992), (100.0%, 100.0%, 1.000), (100.0%, 100.0% , 1.000), (97.24%, 98.21%, 0.9773) 和 (98.77%, 99.53%, 0.9915)。显然,我们的方法成功地识别了大部分真正的对应关系,只有少数被错误分类。这些结果证明了我们方法的普遍性和鲁棒性,即使存在大量异常值,它也可以处理不同的场景。

图4. 我们的 mTopKRP 在 10 个具有代表性的遥感图像对上的特征匹配结果。 (从上到下、从左到右)UAV1、UAV2、SAR1、SAR2、PAN1、PAN2、CIAP1、CIAP2、FE1 和 FE2。十对图像中的内点比例分别为 42.49%、41.40%、36.05%、42.99%、26.88%、27.26%、13.28%、15.76%、50.30% 和 15.45%。运动场中每个箭头的头尾对应两幅图像中特征点的位置(蓝蓝=真阳性,黑色=真阴性,绿绿=假阴性,红红=假阳性)。为了可见性,在图像对中,最多显示 100 个随机选择的匹配项,并且不显示真正的否定项。最好以彩色观看。
4.3 定量结果
为了测试特征匹配方法在不同场景下的性能,我们将五个数据集分为三组。 SAR 和 CIAP 被分类为刚性数据集,UAV 和 PAN 被归类为投影数据集,FE 被归类为非刚性数据集。这三个数据集的平均推定匹配数分别为 939.43、888.94 和 463.00。对这三组进行了定量实验,结果分别报告。图 5 的第一行提供了三个数据集上初始内点比率的累积分布。我们看到,对于刚性数据集,内点比率通常很高,少数图像对由于内点低而具有挑战性比率。对于投影数据集,内部比率分布是两极分化的,容易的和具有挑战性的是平衡的。对于非刚性数据集,图像对保持相对较高的内点比率,但是,由于其非刚性性质,该数据集仍然具有挑战性。
图 4 总结了三个数据集的统计结果,例如精度、召回率、F-score 和运行时间。从左到右,每列显示刚性数据集、投影数据集、和非刚性数据集,分别。对于刚性数据集,我们看到所有方法都取得了很好的效果。这是由于图像对之间的简单转换模型。 ICF 的精度相对较低,因为它是为非刚性特征匹配而设计的,并且放宽了空间约束。尽管 GS 和 RANSAC 实现了很高的准确性,但我们的方法显示了它能够保留更多正确匹配,从而带来更好的召回率。 LLT 也有比较结果,但是,它需要数据的先验,其中必须手动设置模型。结果还表明,我们的方法比 LPM 有显着改进。这两种方法的召回率很接近,但是,随着我们对局部结构的改进解释,我们的方法比 LPM 获得了更好的精度。性能通过汇总统计量(例如 F 分数)清楚地表征。我们可以观察到我们的方法是最好的,具有明显的优势。对于投影数据集,情况略有变化。 ICF 显示其在保留正确匹配方面的弱点,导致召回统计数据不佳。除了 ICF,所有方法都表现出很好的性能。由于对异常值的鲁棒性,我们的方法仍然是最好的。
在精度和召回率方面,我们的方法始终获得出色的结果,而其他方法的鲁棒性较差,在某些情况下会失败。对于非刚性数据集,我们可以观察到 LPM、LLT 和 mTopKRP 的性能最好。这是因为已知 GS 和 RANSAC 对非刚性变形很敏感,而 ICF 的召回率总是很低。与 LPM 和 LLT 相比,我们的方法显然获得了最佳性能,这证明了它的有效性。图 5 还给出了不同方法的时间成本。我们的方法复杂度相对较低,如累积分布的后半部分所示,仅次于 LPM。这个结果符合我们的预期,因为我们的方法是基于有效的 LPM 方法。总之,我们的方法在效率方面具有优势。
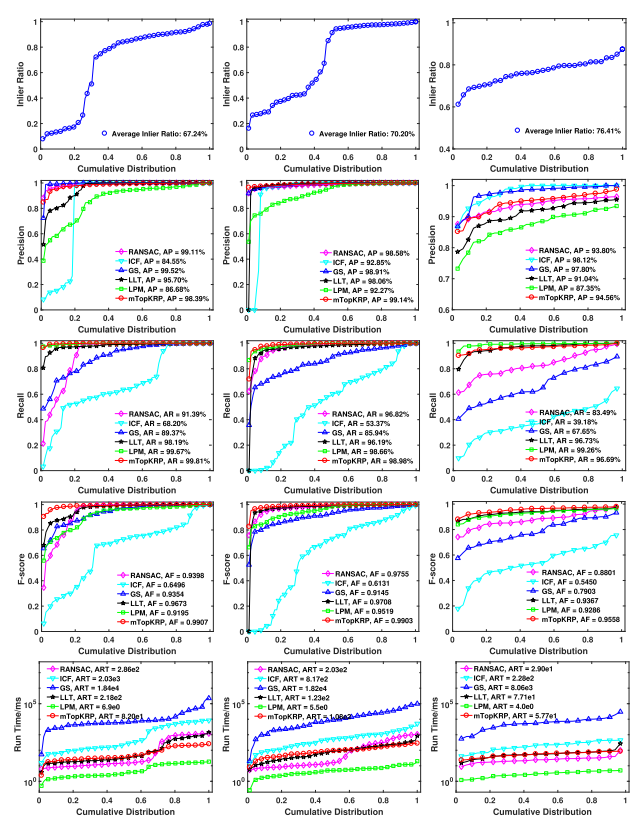
图5. RANSAC [14]、ICF [24]、GS [33]、LLT [1]、LPM [16] 和我们的 mTopKRP 在五个图像集上的定量比较,根据它们的变换模型分为三组。 (从左到右)刚性(SAR、CIAP)、投影(UAV、PAN)和非刚性(FE)。 (从上到下)相对于累积分布的初始内点比率、精度、召回率、F 分数和运行时间。曲线上坐标为 (x, y) 的点表示有 (100 * x)% 的图像对具有性能值(即内点率、精度、召回率、F 分数或运行时间)不超过 y。图例中报告了 AP、平均召回率 (AR)、AF 和 ART。
5. 总结
在本文中,我们提出了一种简单而有效的失配去除方法,用于遥感图像的鲁棒特征匹配,称为 mTopKRP,该方法基于同一对象或场景的两幅图像之间特征对应的稳定相邻拓扑关系。在 mTopKRP 中,我们使用 K-NN 排序列表来表示要匹配的特征点的拓扑。然后重新定义和改进加权的 Spearman 足迹距离,以测量图像对的两个前 K 排名列表之间的相似性。同时,我们将特征匹配任务表述为一个迭代优化问题,并引入了一种封闭形式的解决方案,可以在线性时间复杂度上建立可靠的对应关系。各种遥感图像的定性和定量结果证明了我们处理遥感和摄影测量中各种匹配任务的方法在现有技术上的通用性、鲁棒性和优越性能。此外,它的时间成本低,只需要几十毫秒来处理超过 1000 个假定的匹配,对于处理实时或大规模任务具有重要意义。