PSO-SIFT：基于改进SIFT和增强特征匹配的遥感图像配准

Remote Sensing Image Registration With Modified SIFT and Enhanced Feature Matching

PSO-SIFT：基于改进SIFT和增强特征匹配的遥感图像配准

Remote Sensing Image Registration With Modified SIFT and Enhanced Feature Matching | IEEE Journals & Magazine | IEEE Xplore

IEEE Xplore Full-Text PDF:

摘要：

尺度不变特征变换算法及其各种变体在基于特征的遥感图像配准中得到了广泛的应用。然而，在某些情况下，可能难以为在强度映射中表现出显著差异的远程图像对找到足够正确的对应关系。在这封信中，一个新的梯度定义，以克服图像之间的远程图像对强度的差异。然后，通过结合每个关键点的位置、尺度和方向，引入增强的特征匹配方法，以增加正确对应的数量。所提出的算法进行了测试多光谱和多传感器遥感图像。实验结果表明，与现有的几种匹配方法相比，该方法在正确匹配数目和对齐精度方面都有较大的提高.

关键词：特征匹配，图像配准，遥感，尺度不变特征变换。

1 引言

图像配准是将同一场景的不同时间、不同传感器和不同视点的两个或多个图像进行匹配的过程[1]。它是许多遥感任务不可缺少的一部分，如变化检测，图像融合，环境监测。

遥感图像配准的方法很多.这些方法可以粗略地分为两类：基于强度的方法和基于特征的方法[1]，[2]。基于强度的方法使用像素强度之间的相似性来确定两个图像之间的对齐。主要使用的相似性度量是互相关和互信息[2]。然而，基于强度的方法受到单调纹理[3]、光照差异和全局优化的高度计算复杂性[4]的影响。基于特征的方法提取显著特征，并使用这些特征之间的相关性来确定最佳对齐。一般来说，这些特征包括点、边缘、轮廓、特定区域的质心[5]、[6]等。在基于特征的方法中，尺度不变特征变换（SIFT）[7]是经典算法。SIFT具有图像缩放和旋转不变性以及部分光照和摄像机视点变化不变性，已成功应用于可见光图像的配准。在基于特征的方法中已经进行了一些其他改进，例如SURF [8]，GLOH [9]和BRISK [10]。这些改进主要是为了提高计算效率。然而，当SIFT直接应用于遥感图像时，由于强度映射的显著差异，正确对应的数量不足以确认匹配精度[4]。强度映射可以是线性的、非线性的和不稳定的。为了克服这个问题，Li等人[4]提出了鲁棒SIFT（R-SIFT），其中每个像素的梯度方向被细化，并且更多的主方向被分配给每个关键点。在特征匹配过程中，引入尺度-方向联合约束准则，提高了匹配性能。Kupfer等人。[11]提出了一种快速模式搜索SIFT（MS-SIFT）算法，该算法利用SIFT特征的尺度，方向和位置信息，然后有效地去除不精确的SIFT关键点对应关系。Sedaghat等人[3]提出了统一R-SIFT（UR-SIFT）算法。UR-SIFT方法有效地生成足够鲁棒、可靠和均匀分布的对齐关键点。Gong等人[2]提出了一种用于自动图像配准的粗到精方案。粗略的结果为优化器在微调过程中提供了一个接近最优的初始解。

在这封信中，我们提出了一个新的梯度定义，以克服图像之间的远程图像对强度的差异。此外，提出了一种鲁棒的点匹配算法，该算法结合每个关键点的位置、尺度和方向来增加正确对应的数量。该算法的灵感来自SIFT算法，将被称为PSO-SIFT。本文提出了一种在遥感图像配准中广泛应用的相似性变换模型。在第二节中，概述了经典的SIFT算法及其在遥感图像上的局限性。在这封信中提出的算法在第三节。在第四节中给出了在三个不同的遥感图像对上的实验结果。结论意见载于第五节。

2 背景

基于SIFT的配准算法由三个主要模块组成：关键点检测、描述符提取和关键点匹配。构造了高斯尺度空间的差分，作为高斯拉普拉斯算子的近似。然后选择三维中的局部极值作为候选关键点。每个关键点基于梯度方向的局部直方图被分配一个或多个主方向。然后，将128个元素的描述符分配给每个关键点。SIFT特征由局部$(x_i,y_i)$、尺度$s_i$、方向$\theta_i$和描述符$d_i$四个分量组成，最后一个模块以描述符上的最小欧氏距离作为关键点匹配准则。关于SIFT的更多细节可以在[7]中找到。

图1（a）和（B）示出了在两个不同波段和不同传感器设备中获取的多光谱图像。因此，它们具有非常不同的强度映射，并且通常更难以配准。图2示出了图1（a）和（B）中匹配的原始SIFT关键点的尺度比、主方向差、水平移位和垂直移位的直方图。关键点的匹配是通过对应描述符的最近邻和次最近邻之间的欧氏距离之比来实现的。该比率的阈值被设置为$d_{ratio}$。直方图的详细参数设置见[11]。我们可以看到，除了比例直方图外，四个直方图不能明显地表现出单一的模式，这是由于多光谱图像与多光谱遥感图像中相同区域之间的强度映射的差异，可能具有显著的非线性强度差异[4]。这样的强度差异将导致期望被正确匹配的对应的不同的主取向差异。此外，特征描述符对这些差异不鲁棒，因为在描述符提取过程中使用每个关键点的主方向以确保旋转不变性。

Fig. 1.遥感图像对。(a)Landsat-7 ETM+，波段5。(b)Landsat 4-5 TM，波段3。©陆地卫星TM，波段5。(d)谷歌地球，光学。(e)阿罗斯帕尔萨。(f)大地卫星ETM+，波段5。

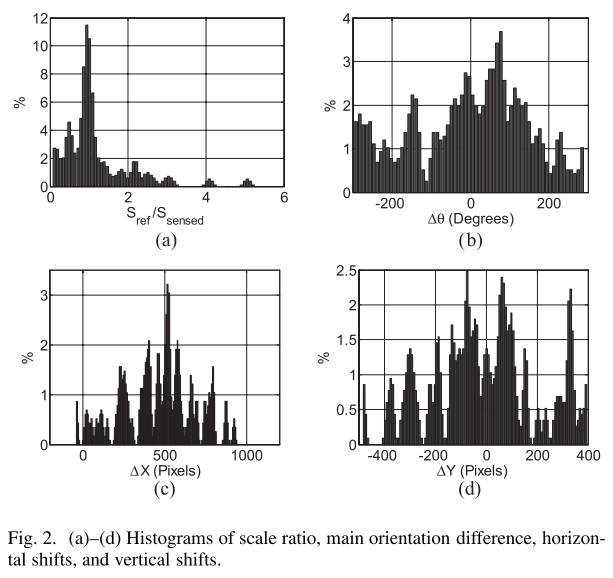
图二.(a)- （d）比例尺比率、主要方向差异、水平移位和垂直移位的直方图。

3 提出的方法

3.1 新的梯度定义

亮度映射的显著差异会导致同一区域的遥感图像对之间的梯度方向和梯度大小不同。因此，预期被正确匹配的SIFT对应将不具有最小欧几里得距离，因为对应计算取决于由关键点位置周围的梯度方向和梯度幅度形成的描述符。为了使描述符更强大的差异，我们提出了一个新的梯度定义（包括方向和幅度）的高斯尺度空间中的每个像素。为了提高算法的效率，不对输入图像对进行扩展，而是利用原始输入图像构建高斯金字塔的最低层。首先，我们通过Sobel滤波器计算高斯尺度空间图像的梯度幅度，

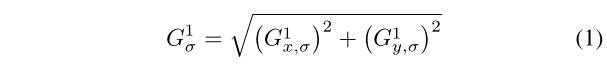
其中，$σ$是高斯尺度空间的尺度，$G_{x,\sigma}^1$和$G_{y,\sigma}^1$分别表示高斯尺度空间图像在尺度$σ$下的水平和垂直导数。然后，我们将所提出的梯度方向和梯度幅度定义为：

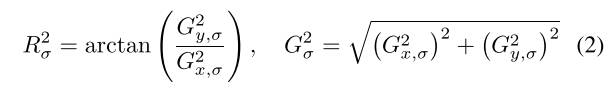
其中$G_{x,\sigma}^2$和$G_{y,\sigma}^2$分别表示高斯尺度空间的梯度幅度图像$G_{\sigma}^1$的水平和垂直导数。所有的衍生物近似的Sobel滤波器。使用Sobel算子，导数[12]，[13]很容易计算。注意，由（2）计算的梯度用于方向分配和描述符提取的处理中。在这封信中，我们在计算直方图时不使用梯度幅度的高斯加权[14]。与原始SIFT描述符中使用正方形邻域和4×4正方形扇区不同，我们使用类似GLOH的[9]，[14]圆形邻域（半径为12$σ$）和对数极坐标扇区（17个位置箱）来创建特征描述符。一系列的实验表明，GLOH获得了最好的结果[9]。注意，梯度方向在八个仓中被量化。这导致136维描述符。图4（a）示出了该方法。

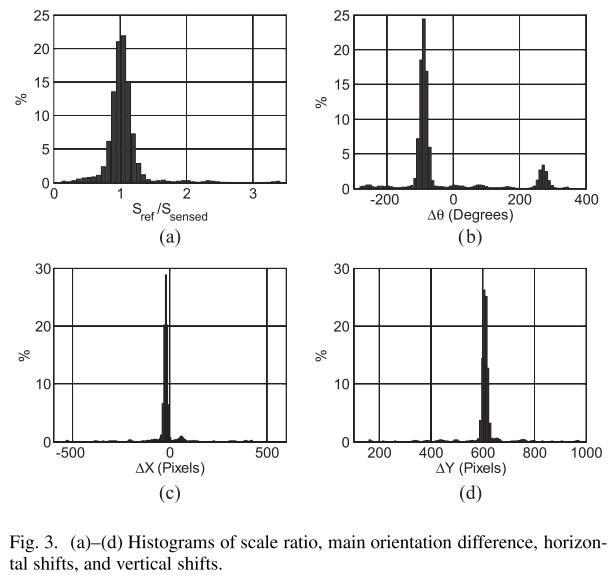
图三.(a)- （d）比例尺比率、主要方向差异、水平移位和垂直移位的直方图。

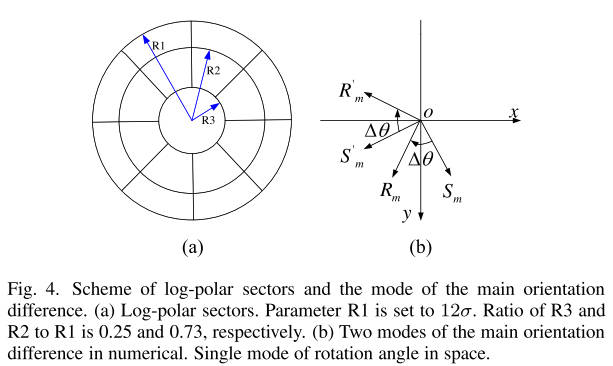
见图4。对数极扇区方案和主方位差模式。(a)对数极坐标扇区。参数R1设置为12σ。R3和R2与R1之比分别为0.25和0.73。(b)两种模态的主要取向在数值上存在差异。空间旋转角度的单一模式。

图3示出了在应用所提出的梯度定义之后，图1（a）和（B）中的匹配关键点的尺度比、主方向差、水平移位和垂直移位的直方图。与图2中的结果相反，除了具有两个主模式的主方向差直方图之外，这些直方图明显地表现出单一模式。主方位差直方图具有两个主要模式的原因是，圆周角在-180 °和180 °内不连续[见图4（B）]。需要指出的是，旋转角只有一个主模态。如果我们知道两个主要模型的位置之一，则另一个模型的位置可以计算为

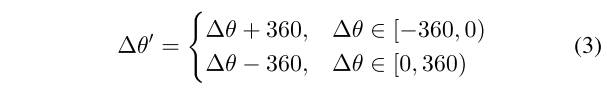
其中$\Delta\theta$和$\Delta\theta'$分别表示主取向差直方图的两个模式的位置。图4（B）示出了主取向差的两种模式和旋转角的单一模式。标度比的众数很容易位于$r =1.022$处。主方位差的两个模位于$\Delta θ = −89.61$和$\Delta θ' = 270.97$处，水平位移和垂直位移的模位于$\Delta x = −10.96$和$\Delta y = 608.76$处。请注意，模式的确切位置是通过适当的插值方法[11]获得的。$\Deltaθ$和$\Deltaθ'$之间的关系与（3）的结果非常接近。最后，我们使用快速样本一致性（FSC）算法[15]分别获得转换模型参数$r =0.99$，$\Delta θ = −90$，$\Delta x = − 9.71$和$ \Delta y = 604.75$。从以上结果和分析可以看出，新的梯度计算方法更好地处理了遥感图像对的亮度差异问题。

3.2 增强的特征匹配

相似变换由三个参数组成：平移、缩放和旋转。在相似性变换模型下，在大多数情况下，正确匹配的对将具有相同的空间旋转角度、相同的缩放比、相同的水平移位和相同的垂直移位。因此，我们使用固有信息（即，位置、比例和主方向），以增加正确对应的数量。

已经分别从参考图像和感测图像中提取了两个点特征集$P=p_1,p_2,...,p_M$和$P'=p_1',p_2',...,p_N'$。$(x_i,y_i)$、$s_i$和$θ_i$分别表示参考图像中的关键点$p_i$的位置、尺度和主取向。$(x_i'，y_i')$、$s_i'$和$θ_i'$分别表示感测图像中的关键点$p_i'$的位置、尺度和主取向。对应$p_i$和$p_i'$的位置变换误差表示为：

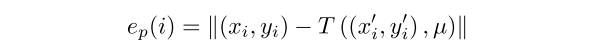
其中$T((x_i',y_i'),\mu)$是相似性转换模型，μ是转换模型参数。我们还使用点$p_i$和$p_i'$的尺度误差[4]和相对主方位误差[4]作为

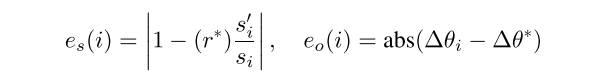
其中，$r^*$和$\Delta\theta ^*$分别表示参考图像和感测图像之间的比例比和主取向差的模式位置，并且$\Delta\theta_i=\theta_i-\theta_i'$表示$p_i$和$p_i'$之间的主取向差。然后，我们定义一个更鲁棒的关节距离，称为位置尺度方向欧几里得距离（PSOED），

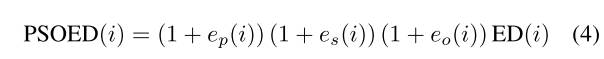
其中$ED(i)$表示对应于关键点$p_i$和$p_i'$的描述符的欧几里德距离。在大多数情况下，当点对正确匹配时，PSOED将最小化。下面给出所提出的匹配算法。

1. 初始匹配：关键点的匹配是通过对应描述符的最近邻和次最近邻之间的欧氏距离之比来实现的。将比例阈值设为$d_{ratio}$，得到对集$PP$，并建立了比例、主方向差、水平位移和垂直位移的直方图。模式位置$r^*$、$\Delta\theta ^*$、$\Delta x^*$和$\Delta y^*$从直方图获得。FSC算法[15]用于从对集合$PP$计算初始变换参数$\mu$。
2. 重新匹配：由于主方向差直方图具有两种模式，因此仅存在$r^*$、$\Delta\theta ^*$、$\Delta x^*$和$\Delta y^*$的两种不同组合。对于每种模式组合，我们使用$PSOED$作为距离度量，并通过最近邻和次最近邻之间的距离之比来匹配关键点。比率的阈值表示为$d_r$。由于匹配执行两次，参考图像或感测图像中的关键点将在另一图像中具有一个或多个匹配;因此，我们将具有最小PSOED的点对作为候选匹配对。然后，获得关键点对集合$PP_1$。
3. 离群值删除：$PP_1$中会有一些错误的对应关系。因此，我们首先使用MS-SIFT [11]中提出的方法来过滤掉大多数离群值。令$(x_1,y_1)$和$(x_1',y_1')$表示集合$PP_1$中的对应关键点的坐标。对应关键点的水平和垂直移位被定义为：

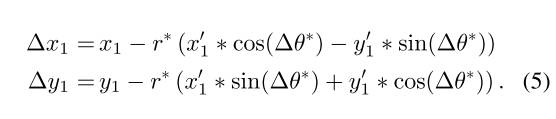
​ 然后，根据以下逻辑过滤器[11]消除大多数离群值：

​

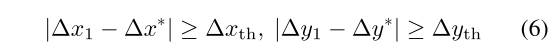
其中，$\Delta x_{th}$和$\Delta y_{th}$分别表示水平差和垂直差的阈值。阈值被设置为相应直方图的区间宽度[11]。最后，我们从$PP_1$得到一个关键点对集合$PP_2$，并使用FSC算法[15]从关键点对集合$PP_2$中找到正确的对应。

请注意，尽管我们需要在初始匹配步骤中计算每个关键点对的欧几里得距离，但我们在重新匹配步骤中保存了计算工作量。为了更好地显示直方图的分布，$d_{ratio}$设置为0.9。为了尽可能多的候选关键点对，$d_r$被设置为0.9 [4]。在离群值去除步骤中采用的FSC算法可以在更少的迭代中获得比随机样本共识[16]更多的正确匹配。

4 实验与结果

4.1 测试图像对

为了对所提方法进行评估，我们测试了三个图像对。这些图像对如图1所示。第一对P-A是美国地质调查局项目[17]的多光谱图像，经纬度：69.6/−92.7，分辨率240米。选择来自第5波段(传感器：Landsat-7ETM+，日期：2000/7/24)的大小为614×611的片段作为参考图像。为了增加测试数据集的难度，选择了模拟旋转90◦后的波段3(传感器：Landsat 4-5TM，日期：1999/6/28)的ASI614×611片段作为传感图像。第二对P-B是两个412×300多传感器图像，参考图像是从Landsat-TM传感器于1995年9月拍摄的场景的第5波段获得的(空间分辨率为30m)，而遥感图像是从Google Earth获得的光学图像(空间分辨率为5m)。第三对P-C是两幅800×800多传感器图像，参考图像来自ALOSPALSAR2010年6月5日在不列颠哥伦比亚省坎贝尔河地区(初始空间分辨率为15 m重采样到30 m)拍摄的场景的HH模式(L波段)，遥感图像来自LANDSAT-ETM+于1999年6月26日在同一区域(空间分辨率为30 m)拍摄的场景的5波段(1.55-1.75μm)。

4.2 评价标准

1. 匹配精度：通过均方根误差（rmse）标准评价精度[2]，[11]。从参考图像和感测图像中手动选择总共N个对应点对$\{(x_i,y_i),(x_i',y_i')\}$。点对经过精心选择和优化，以尽可能降低残差[2]。因此，这些点对被用来作为参考，以测试模型参数的精度。rmse根据以下公式计算：

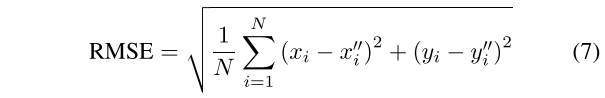
​ 其中$(x_i'',y_i'')$表示$(x_i',y_i')$的变换坐标。对于每个测试图像对，该算法被执行十次，并且计算十个 结果的平均值作为最终结果。

2. 关键点数量：正确对应的数量被用作评估所提出方法的鲁棒性的标准[18]。调整了关键点检测的阈值，因此比较方法和所提出的方法具有大致相同的检测点数量。

4.3 实验结果

我们将所提出的PSO-SIFT算法与基于SIFT的FSC算法、SURF、SAR-SIFT [14]和MS-SIFT算法进行了比较。虽然SAR-SIFT算法是专门针对SAR图像设计的，但它对其他类型的遥感图像表现出良好的性能。除了SURF之外，其他方法都是在MATLAB R2012 a下实现的，采用Intel Core 2.53-GHz处理器和6 GB物理内存。源代码可以在https://github.com/ZeLianWen/Image-Registration上找到。

表I显示了三个测试对的匹配精度、正确匹配的关键点数量和平均运行时间的结果。注意，该算法执行十次，并且十次运行时间的平均值作为最终运行时间。在两个不同的频带和不同的传感器设备中采集测试对P-A。由于光谱波段的不同，遥感图像对之间的亮度映射存在着一些不规则的关系。考虑到表I中的结果，SIFT、SAR-SIFT和SURF未能配准测试对P-A。然而，我们修改后的梯度计算方法，121个正确匹配的关键点被过滤，并实现亚像素匹配的结果，这表明新的梯度定义的鲁棒性。MSSIFT方法虽然能准确地匹配测试对P-A，但很难调整其参数以获得满意的结果。测试对P-B和P-C是由不同的传感器设备获得的，并且在远程图像对之间存在图像强度的单调关系。SIFT、SURF、SAR-SIFT和MS-SIFT等方法都能准确地匹配这对图像，表明这些方法对单调强度变换具有不变性。所提出的梯度计算方法也达到亚像素精度。为了验证增强的特征匹配方法的鲁棒性，我们比较了两种算法，即建议梯度+ FSC和建议梯度+增强匹配。可以清楚地看到，增强的匹配方法有效地增加了正确匹配的关键点的数量。对于测试图像对P-A，增强匹配的RMSE虽然比FSC稍高，但也达到了亚像素精度。证明了FSC算法的鲁棒性。由于SURF是基于C++语言实现的，所以效率很高。两个图像对的匹配结果如图5所示。与FSC匹配方法相比，改进的匹配方法大大提高了正确匹配率。棋盘格镶嵌图像如图6所示。可以看出，两幅图像的边缘和区域精确重叠，这证明了我们提出的方法的准确性。

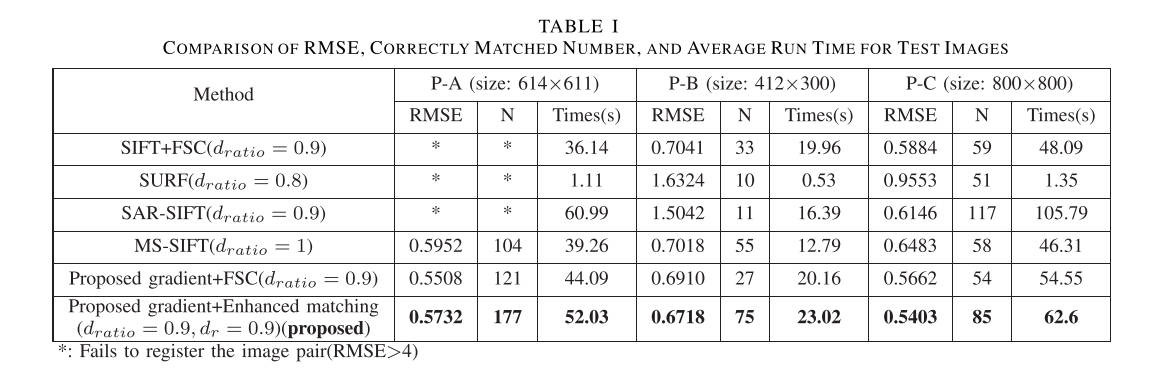
表I 试验样本的RMSE、正确匹配数和平均运行时间的比较

图五.图1的匹配结果。(a)及（c）建议坡度+ FSC。(b)和（d）拟议的梯度+增强匹配。

见图6。所提出的方法对纸板图像进行拼接。(a)图像对P-A的结果。(b)图像对P-B的结果。©图像对P-C的结果。

5 结论

在这封信中，我们提出了一种新的梯度计算方法，是更强大的复杂的非线性强度变换的遥感图像。此外，已经提出了一种鲁棒的点匹配算法，该算法结合每个关键点的位置、尺度和方向来增加正确对应的数量。多光谱和多传感器遥感图像上的实验结果表明，我们的方法显示出更好的性能比国家的最先进的方法在对齐精度和正确匹配的关键点的数量在某些情况下。