RIFT:基于辐射变化不敏感特征变换的多模态图像匹配

RIFT:Multimodal image matching based on radiation-variation insensitive feature transform
RIFT:基于辐射变化不敏感特征变换的多模态图像匹配
摘要:
传统的特征匹配方法,如尺度不变特征变换(SIFT),通常利用图像强度或梯度信息来检测和描述特征点; 然而,强度和梯度都对非线性辐射畸变(NRD)敏感。 为了解决这个问题,本文提出了一种对大 NRD 具有鲁棒性的新颖特征匹配算法。 所提出的方法称为辐射变化不敏感特征变换(RIFT)。 RIFT 中有三个主要贡献。 首先,RIFT 使用相位一致性(PC)而不是图像强度来进行特征点检测。 RIFT同时考虑特征点的数量和重复性,并检测PC地图上的角点和边缘点。 其次,RIFT最初提出了最大索引图(MIM)用于特征描述。 MIM 由 log-Gabor 卷积序列构造而成,对 NRD 比传统梯度图鲁棒性更强。 因此,RIFT不仅大大提高了特征检测的稳定性,而且克服了梯度信息对于特征描述的限制。 第三,RIFT分析了旋转对MIM值的内在影响,实现了旋转不变性。 我们使用六种不同类型的多模态图像数据集来评估 RIFT,包括光学光学、红外光学、合成孔径雷达 (SAR) 光学、深度光学、地图光学和昼夜数据集。 实验结果表明,RIFT在多模态图像上优于SIFT和SAR-SIFT。 据我们所知,RIFT 是第一个能够在上述所有类型的多模态图像上取得良好性能的特征匹配算法。 RIFT 的源代码和多模态图像数据集已公开。(http://www.escience.cn/people/lijiayuan/index.html)
关键词—多模态图像匹配、非线性辐射畸变 (NRD)、特征匹配、最大索引图 (MIM)、相位一致性 (PC)。
1 引言
图像特征匹配是摄影测量和遥感中的一个基本且关键的问题,其目标是从两个或多个具有重叠区域的图像中提取可靠的特征对应关系[1]。 它还广泛应用于计算机视觉[2]、[3]、机器人视觉[4]、[5]、医学图像分析[6]等领域。 图像匹配一直是研究的热点问题,并在过去几十年中取得了长足的进展。 然而,图像匹配,特别是遥感图像匹配,仍然是一个病态问题,存在许多不确定性。 一般来说,遥感图像对可能包含尺度、旋转、辐射度、噪声、模糊或时间变化[7]。 这些几何和辐射的巨大差异对当前的图像匹配算法提出了严峻的挑战,导致匹配性能大幅下降,难以满足不断变化的实际应用的要求。 因此,研究更有效、通用、鲁棒的图像匹配算法非常重要。 要实现通用的鲁棒图像匹配,需要解决三个难题:(1)对各种几何和辐射畸变的鲁棒性; (2)更高效、更稳健的异常值检测模型; (3)非刚性变形图像匹配问题。 在我们过去的工作中,我们研究了几何扭曲[8]、非刚性匹配[7]、[9]和异常值去除[10]-[12]。 在本文中,我们将重点关注辐射畸变,特别是非线性辐射畸变(NRD)。
辐射畸变是指传感器成像过程中地物光谱发射率与真实光谱发射率不同的现象[13]。 造成辐射畸变的因素是多方面的,可以概括为两个方面[14]:(1)传感器本身的成像特性。 此类误差可以视为系统误差。 同一传感器获取的图像通常具有相同的系统误差,因此对经典图像匹配算法影响很小。 然而,随着传感器和应用的多样化,往往需要融合不同传感器的优势信息,最终实现对场景更加准确可靠的描述。 不同传感器的成像机制可能存在较大差异,对于同一物体所获取的图像具有不同的表达方式,从而导致图像对之间的辐射差异较大。 经典的特征匹配方法仍然能够解决线性辐射差异; 不幸的是,对于 NRD 来说,这些方法可能不起作用。 通常,NRD较大的图像称为多模态图像。 传统方法通常使用强度信息或梯度信息进行特征检测和描述。 然而,图像强度和梯度对 NRD 非常敏感。 可以说,多模态图像的处理是图像匹配的瓶颈问题。 目前,在无法获得图像几何地理信息的情况下,还没有一种图像匹配方法可以同时应用于光学光学匹配、红外-光学匹配、合成孔径雷达(SAR)-光学匹配、深度-光学匹配、地图光学匹配、日间匹配等。 -夜间匹配。 (2)大气引起的辐射传输误差。 在电磁波传输过程中,地物的光谱发射率可能会受到大气作用、太阳高度角和光照条件的影响而发生畸变。 这类畸变在多时相遥感图像中尤为突出,常常表现为“不同物体同光谱”或“同物体不同光谱”现象。 这种非线性差异会降低对应关系之间的相关性,这往往会导致匹配困难。 由于多模态、多时相遥感影像数据在目标检测、灾害评估、违法建筑检测、土地资源变化监测等方面发挥着重要作用,因此研究针对大辐射差异尤其是大NRD的影像匹配方法势在必行。
在本文中,我们提出了一种基于相位一致性(PC)和最大索引图(MIM)的辐射不敏感特征匹配方法,称为辐射变化不敏感特征变换(RIFT)。 首先,我们检测PC地图上的角点特征点和边缘特征点。 我们发现角点特征通常具有更好的重复性并且边缘特征的数量较多。 因此,角点特征和边缘特征的结合可以提高特征检测的稳定性。 然后,我们构建了基于 log-Gabor 卷积序列的 MIM,它比传统的梯度图对 NRD 具有更强的鲁棒性。 因此,MIM非常适合多模态图像特征描述。 然而,MIM 对旋转非常敏感。 不同的旋转角度可能会导致不同的MIM。 我们分析了旋转对 MIM 值的内在影响,并通过构造多个 MIM 实现旋转不变。 实验表明,RIFT 在多模态图像上远远优于不变特征变换(SIFT)[15]和 SAR-SIFT [16]。 据我们所知,RIFT 是第一个可以在所有不同类型的多模态图像上取得良好性能的特征匹配算法。
2 相关工作
图像匹配是摄影测量和遥感产品自动化生产中最重要的步骤之一,其结果直接影响图像拼接、束平差、3D重建等应用。 参考文献[1]对传统图像匹配方法进行了非常系统的总结和分类。 根据这个总结,图像匹配方法可以分为两类:基于区域的匹配方法和基于特征的匹配方法。
2.1 基于区域的方法
基于区域的匹配方法使用原始像素值和特定的相似性度量来查找图像对之间的匹配关系。 通常,使用预定义的局部窗口或全局图像来搜索匹配,并且不需要特征提取阶段[17]。
基于区域的方法的缺点之一是它们仅适用于包含平移变化的图像对。 对于包含旋转变化的图像对,需要圆形窗口来执行相关性。 然而,如果图像对包含复杂的变化,例如旋转、尺度变化、几何扭曲等,这些方法就会失败。
另一个缺点是本地窗口内的内容不明显。 搜索窗口内的图像内容可能相对平滑且缺乏显着特征。 如果搜索窗口位于图像的弱纹理或无纹理区域,则此方法可能会得到不正确的匹配。 因此,窗口选择应根据图像内容而定,选择包含较显着特征的部分作为搜索窗口内容。
基于区域的方法可以大致分为三个子类,包括基于相关的方法[18],[19],基于傅里叶的方法[20],[21]和基于互信息的方法[22],[ 23]。
2.2 基于特征的方法
特征可以更好地描述图像的结构信息,从而降低对传感器噪声和场景噪声的敏感性。 基于特征的方法通常比基于区域的方法更稳健。 在计算机视觉领域,SIFT[15]是最常用、最有效的特征点匹配方法之一。 它首先构造高斯尺度空间并提取尺度空间中的特征点。 然后,SIFT使用梯度直方图技术来描述特征。 加速鲁棒特征(SURF)[24]基于Hessian矩阵提取特征点,并引入积分图技术来提高效率。 主成分分析SIFT(PCA-SIFT)[25]采用主成分分析算法对SIFT描述符进行降维,提取取值较大的维度。 PCA-SIFT大大降低了原始SIFT的复杂度。 Affine-SIFT (ASIFT) [26] 通过模拟两个相机轴方向参数,将 SIFT 扩展为仿射变换的不变性。 ORB(Oriented FAST and Rotated Brief)[27]算法使用加速分段测试(FAST)[28]中的特征来提取特征点,并利用方向二元鲁棒独立基本特征(BRIEF)[29]算法进行特征描述。 该方法时间复杂度低,适合实时应用,但不是尺度不变的。 在摄影测量和遥感领域,SIFT算法由于其对光照、旋转、尺度、噪声和视点变化的鲁棒性也被广泛采用。 然而,由于遥感图像是由不同传感器、不同时间、不同视点拍摄的,遥感图像对之间存在较大的几何畸变和辐射畸变。 为了解决这个问题,学者们提出了许多改进算法。 均匀鲁棒SIFT(UR-SIFT)[30]研究SIFT特征点的分布,并提出一种基于熵的特征点选择策略来提高分布均匀性。 统一能力(UC)检测器[31]提出了一种基于加权排名过程的新颖能力标准,该标准考虑了特征的鲁棒性、规模和空间显着性。 因此,它比 Harris [32] 检测器、SIFT 检测器、SURF 检测器和最大稳定极值区域(MSER)[33] 检测器具有更好的位置分布和匹配质量。 SAR-SIFT[16]根据SAR图像的具体特征引入了新的梯度定义,以提高对散斑噪声的鲁棒性。 自适应分箱SIFT(AB-SIFT)[34]采用自适应分箱梯度直方图来描述特征点,使其更能抵抗局部几何失真。 Sedaghat 和 Mohammadi [35] 结合改进的 SURF 检测器和 AB-SIFT 进行特征匹配,并提出了用于异常值去除的局部图变换。 叶等人。 [36]提出了一种特征检测器(MMPC-Lap)和一种名为局部定向相位一致性直方图(LHOPC)的特征描述符,用于多传感器图像匹配,对光照和对比度变化具有鲁棒性。 然而,这些基于特征的方法对NRD敏感,不适合多模态图像,例如SAR光学、深度光学、地图光学等。
本文旨在解决图像匹配中的辐射畸变问题,特别是NRD问题。 多模态图像是具有NRD的典型图像。 目前,多模态图像匹配的研究主要集中在医学图像上,针对多模态遥感图像处理的研究较少。 然而,多模态遥感图像匹配具有非常重要的理论和实际意义。 从理论上讲,这个问题非常困难,是图像匹配技术的瓶颈问题。 事实上,许多应用需要多模态图像的自动匹配,例如光学图像和SAR图像的信息融合。 在下一节中,我们将简要回顾多模态图像匹配的最新技术。
2.3 多模态图像匹配
最近,多模态图像匹配任务引起了越来越多的关注,并且已经提出了几种算法。 例如,局部自相似描述符(LSS)[37]、部分强度不变特征描述符(PIIFD)[38]、独特的基于顺序的自相似描述符(DOBSS)[39]、ARRSI[40]、定向直方图 相位一致性(HOPC)[41]和相位一致性结构描述符(PCSD)[42]。 其中,ARRSI和HOPC与所提出的RIFT最相似。
ARRSI检测特征点并在PC的最大矩图上进行归一化互相关(NCC)[43]匹配。 尽管 ARRSI 和提出的 RIFT 都使用 PC 度量进行特征检测,但 RIFT 与 ARRSI 有很大不同。 首先,ARRSI不构造特征向量,而是使用NCC来搜索匹配,本质上是一种模板匹配方法,而RIFT是一种特征匹配方法。 其次,RIFT最初提出了一种用于特征描述的MIM度量。 第三,RIFT 对于旋转变化是不变的,而 ARPSI 则不然。
HOPC 扩展了 PC 模型,不仅包含数字信息,还包含相应的方向信息。 然后,基于改进的PC测量和NCC,提出了改进的相似性测量HOPCncc。 不幸的是,HOPC 存在三个主要问题:
- HOPC需要知道图像对应的确切地理信息才能进行几何校正。 然而,在实践中,图像的地理信息可能不够准确或者可能不可用。 例如,卫星图像的地理信息可能与其实际地理位置相距数百米。 在这种情况下,HOPC 就完全无法使用了。
- 虽然HOPC对参考图像进行特征检测,但其本质上是一种模板匹配方法,而不是基于特征的方法,因此对旋转、缩放等敏感。模板匹配方法通常执行2D搜索,这 添加极线约束后变为一维搜索。 HOPC依赖于精确的地理信息,其搜索空间较小,通常是20×20像素的局部窗口。
- HOPC使用Harris检测器来检测特征点。 然而Harris对NRD非常敏感,很难普遍适用于不同类型的多模态图像。 特别是当使用深度图作为参考图像时,Harris的性能变得非常差。 特征检测是特征匹配方法的基础,它决定了两组点之间正确匹配的数量和点定位的准确性。 如果特征数量太少,匹配结果一定很差。
相比之下,RIFT 不依赖于地理信息。 RIFT对NRD具有良好的鲁棒性,无论在特征检测还是特征描述阶段,都实现了旋转不变性。
3 辐射变化不敏感特征变换(RIFT)
在本节中,我们将详细介绍所提出的 RIFT 方法,包括特征检测和特征描述阶段。
3.1 特征检测
经典的特征匹配方法一般依赖于图像强度或梯度信息,即空间域信息。 除了空间域信息之外,还可以使用频域信息来描述图像,例如相位信息。 相位的理论基础是傅里叶变换(FT)定理[44]。 FT可以将图像分解为幅度分量和相位分量。 Oppenheim 和 Lim [45] 首次揭示了相位信息对于保存图像特征的重要性。 相位信息对图像对比度、光照、尺度等变化具有高度的不变性。 此外,Morrone和Owens[46]发现图像中的某些点可以对人类视觉系统引起强烈的响应,并且这些点通常具有高度一致的局部相位信息。 因此,不同角度下局部相位信息的一致性程度称为PC测度。
1)回顾一下 Log-Gabor 滤波器:2D log-Gabor 滤波器(2D-LGF)[47]、[48]通常可以通过 Log-Gabor 滤波器(LGF)垂直方向的高斯扩展来获得。 因此,2D-LGF函数定义如下,
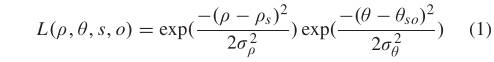
其中表示对数极坐标; 和分别是2D-LGF的尺度和方向; 为2D-LGF的中心频率; 和 分别是 ρ 和 θ 中的带宽。
LGF是频域滤波器,其对应的空域滤波器可以通过傅里叶逆变换得到。 在空间域,2D-LGF可以表示为[41],[49],
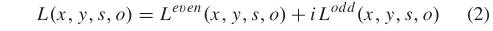
其中实部 Leven(x, y, s, o) 和虚部 Lodd(x, y, s, o) 分别代表偶对称和奇对称 log-Gabor 小波。
2)回忆相位一致性(PC):设I(x,y)表示2D图像信号。 将图像 I(x, y) 与偶对称和奇对称小波进行卷积,产生响应分量 和 ,
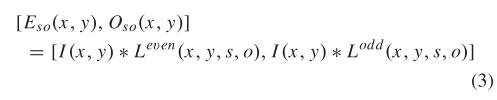
然后,可以得到I(x,y)在尺度s和方向o处的幅度分量 和相位分量 ,
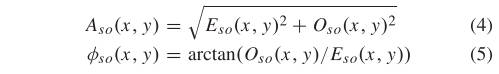
考虑各个方向、各个方位的分析结果,并引入噪声补偿项T,最终的2D PC模型为(更多关于2D PC模型的细节可以参见参考文献[50]):
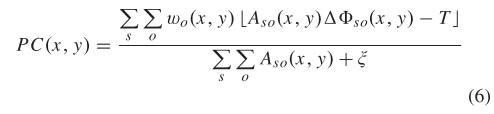
其中 是加权函数; 是一个很小的值; 运算符防止封闭的数量得到负值; 即当封闭数量为负时取零。 是相位偏差函数,其定义为,

where,
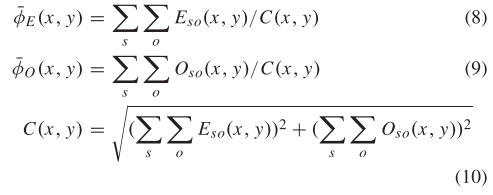
3)角和边缘特征:几种图像匹配方法[51]-[53]已经采用PC测量来进行特征检测。 不同的是,RIFT结合了角特征和边缘特征。 此外,这些方法通常使用SIFT或局部二值模式(LBP)进行特征描述,这些方法对NRD非常敏感,不适合多模态图像。
根据式(6),我们可以获得非常精确的边缘图,即PC图。 然而,这个公式忽略了方向变化对 PC 测量的影响 [54]。 为了得到PC测量和方向变化之间的关系,我们为每个方向o计算一个独立的PC图,其中是方向o的角度。然后我们计算这些PC图的力矩并分析力矩变化 与方向
根据矩分析算法[55],最小矩对应的轴称为主轴,主轴通常表示特征的方向信息; 最大力矩对应的轴垂直于主轴,最大力矩的大小通常反映了特征的独特性。 在计算最小和最大矩之前,我们首先计算三个中间量,
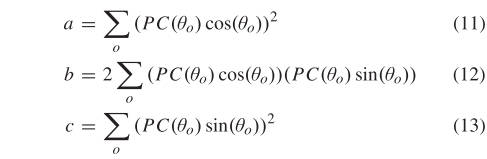
然后,主轴 、最小力矩 和最大力矩 由下式给出:
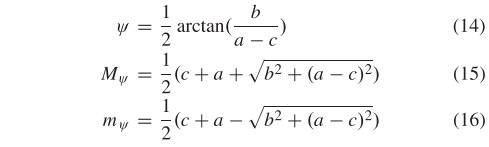
最小力矩 相当于角点检测器中的角点测量值。 也就是说,如果某个点的 值很大,则该点很可能是角点特征; 最大矩是图像的边缘图,可用于边缘特征检测。 具体来说,我们首先计算 PC 映射的 和 。 对于最小矩图,进行局部极大值检测和非极大值抑制,其余点作为角点特征。 由于边缘结构信息具有较好的抗辐射畸变能力,因此我们还使用最大矩图来检测边缘特征点,即对进行FAST特征检测。 因此,该方法综合角点特征和边缘特征进行特征匹配。

图1示出了特征检测的示例,其中图1(a)是一对多模态图像(光学卫星图像和LIDAR深度图); 图1(b)和图1©分别是最小力矩图mψ和最大力矩图Mψ; 图1(d)是FAST[28]特征检测的结果; 图1(e)和图1(f)分别是我们的角特征和边缘特征。 从结果中,我们可以得出几个结论:(1)比较图1(b)和图1(f),我们发现基于图像强度或梯度的传统特征检测器(例如FAST或Harris检测器)非常 对NRD敏感,而PC测度的矩对NRD具有良好的不变性。 通过在PC图的最大矩上执行相同的FAST或Harris检测器可以获得大量可靠的特征点。 (2)从图1(e)可以看出,可以获得明显的角点特征。 但特征点的数量相对较少。 (3)从图1(f)可以看出,最大矩图上可以检测到更多的特征点,但漏掉了很多角点特征。
这样,最小矩图角点特征和最大矩图边缘特征的特征相结合,既保证了特征的高重复性,又保证了特征数量大,为后续的特征匹配奠定了基础。
3.2 特征描述
一旦检测到特征点,就需要进行特征描述,以增加特征之间的区分度。 经典的特征描述符一般使用图像强度或梯度分布来构造特征向量。 然而,如前所述,强度和梯度对 NRD 都非常敏感。 这些描述符不适合多模态图像匹配任务。 上面我们分析了PC测度的特点,其优点是对NRD的鲁棒性。 直观上,使用PC图代替强度图或梯度图进行特征描述更合适。 然而,实验结果并没有达到我们的预期。 具体来说,我们选择了由SAR卫星图像和光学卫星图像组成的图像对进行测试(见图2(a))。 我们首先计算 PC 图(见图 2(b))并检测每个图像的角点和边缘特征(见图 2©)。 然后,对于每个特征,我们基于类似于 SIFT 的分布直方图技术构建特征向量。 基于PC图描述的匹配结果如图2(d)所示。

从图2可以看出,提取的特征数量和分布都很好; 然而,匹配结果很差,因为匹配几乎都是异常值。 这说明PC地图不太适合特征描述。 原因可能如下。 首先,PC 地图中的信息较少,因为 PC 地图中的大多数像素值接近于零。 对于特征描述来说不够鲁棒。 其次,PC图主要包含边缘,对噪声敏感,导致特征描述不准确。 通过这样的分析,我们提出了 MIM 度量而不是 PC 图来进行特征描述。
1)最大索引图(MIM):MIM是通过log-Gabor卷积序列构造的。 卷积序列是在PC图计算阶段获得的。 因此,MIM的计算复杂度非常小。
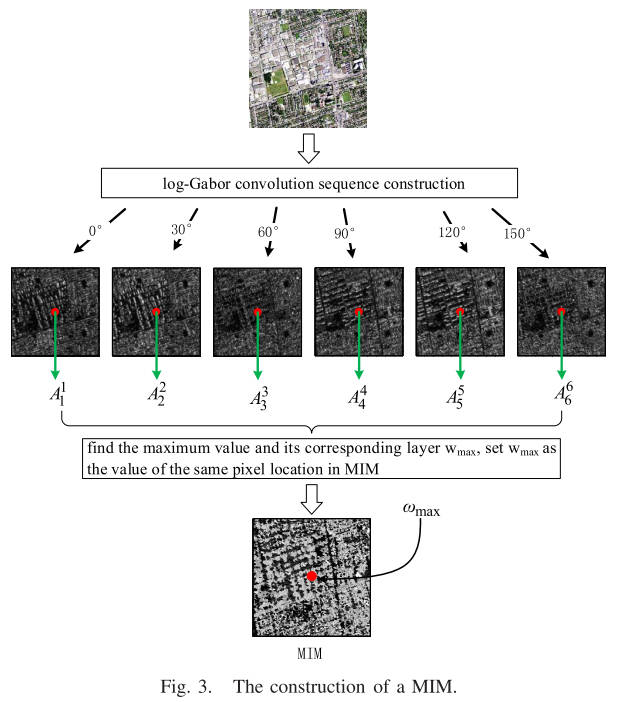
图3说明了MIM的结构。 给定图像 I(x, y),我们首先将 I(x, y) 与 2D-LGF 进行卷积以获得响应分量 和 ; 然后计算尺度 s 和方向 o 处的振幅 。 对于方向o,将所有Ns尺度的振幅相加,得到log-Gabor层,
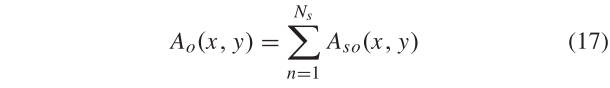
将log-Gabor卷积层按顺序排列得到log-Gabor卷积序列,它是一个多通道卷积图 ,其中为方向数; 上标 表示 log-Gabor 卷积序列的不同通道。 因此,对于卷积图的每个像素位置,我们可以得到一个无维有序数组 。 然后,通过找到该数组中的最大值及其对应的位置通道。 为MIM中位置的像素值。
获得MIM后,我们使用类似于SIFT的分布直方图技术进行特征向量描述。 具体来说,对于每个特征点,我们选择一个以特征为中心的具有 J × J 个像素的局部图像块,并使用标准差等于 J/2 的高斯函数为每个像素分配权重。 如果窗口位置发生变化,此过程可以避免特征描述发生突然变化。 然后,我们将局部块划分为 6 × 6 子网格,并为每个子网格构建一个箱体 的分布直方图,因为 MIM 的值范围从 1 到 。特征向量是通过连接所有直方图获得的。 因此,特征向量的维度为 6 × 6 × 。为了获得对光照变化的不变性,我们最终对特征向量进行归一化。
图2给出了基于MIM描述的匹配示例,其中图2(e)是对应于图2(a)的MIM,图2(f)是匹配结果。 在本实验中,我们设置 = 6,并使用MIM代替传统的梯度进行特征描述。 我们将具有最小欧氏距离的特征点对视为潜在匹配,并应用 NBCS [10] 方法进行异常值去除。 可以看出,即使在 SAR 和光学图像对中,所提出的方法也可以提取大量分布相对均匀的可靠匹配。 SAR与光学传感器的成像机制存在较大差异,导致SAR图像与光学图像之间的NRD较大。 因此,表明所提出的MIM描述符非常适合多模态图像匹配任务,并且比传统的特征匹配方法要好得多。
2)旋转不变性:上一节分析了MIM用于特征描述的可能性和有效性,并描述了特征向量构造细节。 然而,该描述方法假设图像对之间不存在旋转; 也就是说,不考虑旋转变化。 因此,如果图像对中存在旋转变化,则上述方法将不再适用。 因此,必须进行特殊处理,使其具有旋转不变性。 最直接的想法是使用类似于 SIFT 的主导方向方法。 然而,经过大量的实验,我们发现主导取向方法无法实现旋转不变性。
为了分析原因,进行了两个实验。 图4分析了旋转对梯度图的影响,其中图4(a)是LIDAR点云深度图; 图4(d)是将图4(a)顺时针旋转30°得到的;图4(b)和图4(e)是图4(a)和图4(d)的梯度图 ), 分别。 为了消除图4(b)和图4(e)之间的旋转差异,将图4(b)顺时针旋转30°,得到图4(c); 图4(f)是图4(b)和图4(e)之间的差异。 根据图4(f),去除旋转差异后的梯度图基本相同,说明旋转对梯度图的值没有影响。 因此,通过计算特征点的主方向,可以消除局部图像块之间的旋转差异,从而实现旋转不变性。 同样,对MIM也进行上述分析,如图5所示。图5(b)和图5(e)分别是图5(a)和图5(d)的MIM ; 图5©是将图5(b)顺时针旋转30°得到的; 图5(f)是图5(b)和图5(e)之间的差异。 仅当图 5© 与图 5(e) 足够相似时才可以应用主取向方法。 然而,图5(f)的大部分值并不接近于零,这表明图5(c)和图5(e)之间不仅存在旋转差异,而且还存在数值差异,这 数值差异是由旋转引起的。 因此,为了实现旋转不变性,我们必须确定旋转与 MIM 值之间的关系。


如前所述,MIM是基于log-Gabor卷积序列构建的,并且卷积层与方向密切相关。 因此,如果log-Gabor卷积序列的起始层不同,那么构建的MIM就完全不同。
也就是说,两幅图像要想成功匹配,两幅图像对应的log-Gabor卷积序列必须高度相似,并且每一层log-Gabor卷积序列都需要相似。 事实上,log-Gabor卷积序列可以被认为是一个端到端的环形结构,如图6所示。假设图6(a)是一个6层log-Gabor卷积序列环( 由表示)从原始图像(图4(a)中的图像)获得,其中第一层是0°方向卷积结果(卷积序列的初始层); 第二层为30°方向卷积结果,以此类推。 第六层是150°方向卷积结果。 然而,如果我们将图像旋转一个角度(如图6(b)所示),仍然使用0°方向卷积结果作为初始层构造卷积序列(得到卷积序列),由于 由于旋转的影响,初始层的含量将与有较大差异。 事实上,应该使用哪一层作为初始层是未知的,因为它与旋转角度高度相关。 考虑到较小,一般设置为6,我们采用最简单的遍历策略,列出所有可能的场景。 具体来说,我们首先分别为参考图像和目标图像构造一个卷积序列和一个卷积序列。 对于参考图像的,我们直接构造一个MIM();对于目标图像的,我们依次对的初始层进行变换,重建一组具有不同初始层的卷积序列,然后 根据每个卷积序列计算 MIM 以获得一组 。 一般来说,集合 中总有一个与 类似的 MIM。 为了更直观地验证这个结论,我们对图4(d)中的图像进行实验,得到MIM集()。 图7示出了集合中的所有MIM。 的初始层是卷积序列的第一至第六层。 可以看出,如果初始层不同,则生成的 MIM 完全不同。 图8显示了图7和图5©中各子图之间的差异。 发现当使用第六层作为初始层时,构造的MIM 与 非常一致,验证了上述结论。
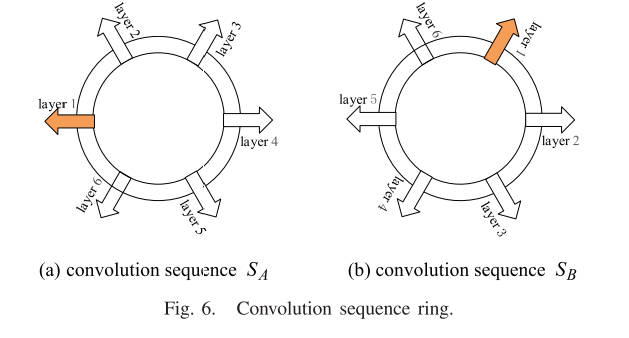

MIM 设置()。 的初始层是卷积序列SB的第一至第六层。

图 8. 图 7 和图 5© 中各子图之间的误差图。
上述过程基本上消除了旋转对MIM值的影响。 然后,可以直接应用主导方向方法来获得旋转不变性。 总之,所提出的 RIFT 算法为参考图像的每个关键点构建了一个特征向量,而没有为目标图像的每个关键点构建了特征向量。
4 实验结果
为了验证所提出的 RIFT 方法的有效性,我们选择了几个多模态数据集进行定性和定量评估。 我们将 RIFT 算法与四种最先进的算法进行比较,即 SIFT、SAR-SIFT、LSS 和 PIFD。 LSS只是一个特征描述符; 因此,我们使用所提出的检测器来提取特征。 为了公平比较,这五种方法的局部描述块的大小设置为相同; 每种比较方法的实现均来自作者的个人网站。 每种方法的参数都经过微调以获得最佳性能,并且在所有实验中都是一致的。
4.1 Datasets
选择六种类型的多模态图像数据集作为实验集,包括光学-光学、红外-光学、SAR-光学、深度-光学、地图-光学和昼夜。 每种类型的数据集包含 10 个图像对,总共 60 个多模态图像对。 样本数据如图9所示。

这些图像对不仅包括多传感器图像和多时相图像,还包括人工生成的图像,例如栅格化地图数据; 不仅有良好光照条件下的图像(白天图像),还有夜间遥感图像; 不仅可以提供高空间分辨率图像,还可以提供中低空间分辨率图像,其GSD范围从0.1米到数百米; 不仅是卫星图像,还有无人机图像,甚至是近距离图像; 不仅有城市图像,还有乡村和山林图像。 这些图像对之间存在严重的畸变,尤其是辐射畸变,这会给图像匹配算法带来巨大的挑战。 这些挑战可以更全面地测试所提出的 RIFT 算法的有效性和鲁棒性。 需要注意的是,RIFT 目前并不是尺度不变的。 因此,每个图像对的两个图像需要重新采样以具有大致相同的 GSD。
为了更好的定量评估,我们需要获得每个图像对之间的地面实况几何变换。 然而,由于各种因素的干扰,真实的数据集通常不具有真正的地面实况几何变换。 通常使用近似地面真值几何变换来进行评估。 具体来说,对于每个图像对,我们选择五个具有亚像素精度的均匀分布的对应关系,并使用这些对应关系来估计准确的仿射变换作为地面真实几何变换的近似。 我们首先对该图像对(RIFT/SIFT/SAR-SIFT)进行特征匹配,并基于NBCS[10]方法去除异常值; 然后,我们计算这些图像对应关系在估计仿射变换下的残差,并将残差小于3个像素的对应关系视为正确匹配。 我们使用正确匹配数(NCM)、均方根误差(RMSE)、平均误差(ME)和成功率(SR)作为评估指标。 注意,如果图像对的NCM小于4,则认为匹配失败。
4.2 参数研究
所提出的RIFT方法包含三个主要参数,即、和。参数是log-Gabor滤波器的卷积尺度数,其值通常大于1。参数是卷积方向数 log-Gabor 滤波器的。 一般来说,方向数越多,构建的MIM的信息量越丰富,计算复杂度也越高。 参数J是用于特征描述的局部图像块的大小。 如果局部补丁太小,则包含的信息不足,不能充分体现特征的独特性。 相反,如果图像块太大,则很容易受到局部几何畸变的影响。 因此,合适的参数非常重要。 本节基于地图光学数据集进行参数研究和灵敏度分析。 我们设计了三个独立的实验来学习参数、和,其中每个实验只有一个参数作为变量,其他参数都是固定值。 实验设置详细信息总结在表 1 中。对于每个参数,我们使用 NCM 和 SR 作为评估指标。 实验结果如表2~表4所示。
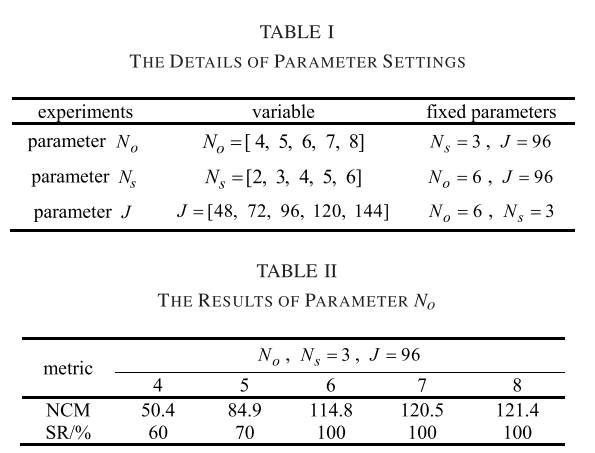
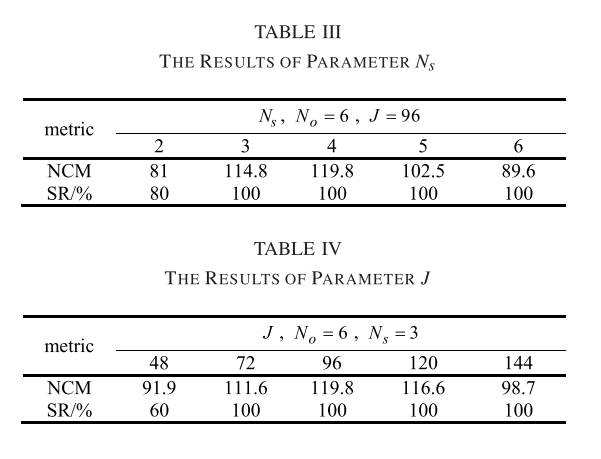
从实验结果可以看出:(1)值越大,构建的MIM信息越丰富,从而获得更多的NCM; 但是,值越大也意味着卷积序列的数量增加,这将大大增加算法的计算复杂度。 由表2可知,当达到6时,RIFT的SR达到100%。 然而,增加方向数量只能略微改善 NCM。 因此,为了兼顾 RIFT 的匹配性能和计算复杂度,我们将 设置为 6。 (2) 从表 3 可以看出, 值较小,SR 精度较低, 值较大,SR 精度较差。 NCM性能。 当 = 4 时,RIFT 在 SR 和 NCM 指标上均达到最佳性能。 虽然 = 3的结果与 = 4的结果仅略有不同,但尺度数量与方向数量不同,增加尺度并不会显着增加计算复杂度。 因此,我们将设置为4。 (3)参数J对RIFT的影响与Ns类似。如果J值很小,则信息量不够丰富,SR和NCM指标会很差; 然而,如果值很大,由于局部几何畸变的影响,NCM的性能会下降。 如表4所示,当 = 96时,RIFT达到最佳性能。为了降低计算复杂度,我们选择 = 72。根据实验结果和分析,这些参数固定为 = 6, = 4,$J $= 72 在下面的实验中。
4.3 探测器评估
我们将 RIFT 检测器与其他六种著名的特征检测器进行比较,包括 FAST [28]、Harris [32]、Brisk [56]、SIFT [15]、SURF [24] 和 MSER [33]。 我们使用可重复性Rep和可以为检测到的特征建立的对应数作为评估指标。 重复性是 与两幅图像 I1 和 I2 中检测到的平均特征数之间的比率 [57],
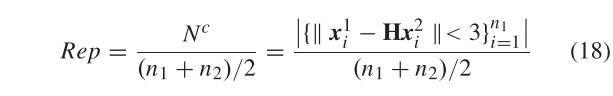
其中 H 是 I1 和 I2 之间的真实变换; 和 分别是 I1 和 I2 中特征的齐次坐标; n1和n2分别是I1和I2中的特征数量; 返回满足 的匹配项数。
我们使用整个 60 多模态图像 对作为评估数据集并计算每个检测器的平均重复性和平均对应数。 结果总结在表5中。我们使用全部60个多模态图像对作为评估数据集,并计算每个检测器的平均重复性和平均对应数。 结果总结在表5中。为了显示每个检测器的稳定性,表5还报告了两个比率指标,即和,其定义如下:
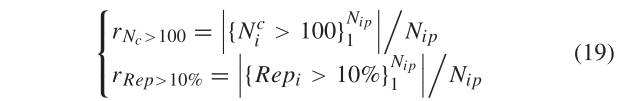
其中是检测器中图像对的数量 评估数据集
如图所示,由于严重的 NRDs,所有检测器在多模态图像数据集上的重复性都很低,这意味着匹配多模态图像对是一项非常具有挑战性的任务。 在这六个探测器中,FAST 和 SURF 的表现比其他探测器要好得多。 FAST 比 SURF 具有更高的重复性并获得更多的对应关系,同时获得更低的$ r_{N_c}>100 r_{Rep}>10%$ 值。 考虑到FAST的性能和效率,我们将其应用在最大矩图上来检测边缘特征。 RIFT 的检测器在所有四个指标中排名最好。 与排名第二的 FAST 相比,它在 Rep 方面提高了 5.5 个百分点,在 方面提高了 179.4 个百分点。
4.4 旋转不变性测试
旋转不变性是所提出的 RIFT 的一个重要特性,这也是与 HOPC 方法相比的一个主要优点。 MIM 和 PC 地图的计算都与方向有关。 所提出的RIFT算法通常沿六个方向(即0°、30°、60°、90°、120°和150°)执行log-Gabor卷积滤波。 这些方向的角度仅在0°到150°之间,这不可避免地引起了人们的担忧:“如果图像对之间的旋转角度不在这个范围内,那么所提出的RIFT是否仍然稳健?”
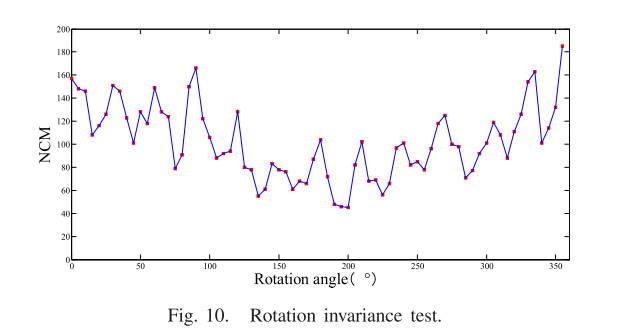
事实上,所提出的RIFT具有非常好的旋转不变性,不仅对于[0°∼150°]之间的旋转,而且对于整个360°范围内的旋转。 为了验证这一结论,从地图光学数据集中选择了图像对进行实验。 该图像对不会受到旋转变化的影响。 首先,我们旋转该图像对的地图。 旋转角度从0°到359°,间隔为5°。 这样,总共得到了72张图(旋转角度为[0°,5°,10°,……,345°,350°,355°,359°])。 这72张地图和光学图像构成了72个图像对。 然后,使用RIFT对这些图像进行一一处理,并将其对应的NCM绘制在图10中。图中的红点代表NCM。 可以清楚地看到,虽然不同旋转角度下的NCM不同,但所有NCM均大于40,表明所提出的RIFT能够成功匹配所有图像对,并且匹配SR准确率为100%,这也验证了 所提出的 RIFT 对于整个 360° 区间的旋转具有良好的旋转不变性。 同时,NCM的差异也表明RIFT的主方向计算可能不是最优的,更鲁棒的特征主方向计算方法将进一步提高所提出的RIFT的匹配性能,这将成为我们的重点研究课题之一 将来。 图11显示了150°旋转和210°旋转的实验结果。 其中,第一行是特征匹配的结果(图中黄线代表正确匹配),第二行是配准结果。 可以看出NCM很大; 匹配点分布比较均匀,配准精度很高。

4.5 匹配性能测试
1)定性比较:我们从六个多模态数据集中选择第一组图像对进行评估,如图9所示。其中,图9(a)包含平移、小旋转和小尺度变化; 图9(b)包括平移变化和90°旋转变化; 图9©、图9(e)和图9(f)包括平移和旋转变化; 图 9(d) 仅包含翻译更改。 由于这些图像对都是多模态图像对,成像机制有很大不同,并且这些图像对包含严重的NRD。 因此,这些图像对的匹配非常具有挑战性。 图 12 分别绘制了 SIFT、SAR-SIFT、LSS、PIIFD 和所提出的 RIFT 的结果。

图12.样本数据的定性比较结果。 图中的红色圆圈和绿色十字线分别表示参考图像和目标图像上的特征点; 黄线和红线分别表示正确匹配和异常值。
如图所示,SIFT 算法无法匹配图 12(a)中的第一、第二和第四图像对。 SR 准确率为 50%。 然而,即使匹配成功,NCM也很小,即24、24和23。由于SIFT算法使用梯度直方图进行特征描述,因此匹配结果很大程度上依赖于图像对梯度图的相似度 。 上述分析表明,梯度图对NRD非常敏感,这是其在多模态图像上匹配性能较差的根本原因。 SARSIFT 算法无法匹配图 12(b)中的第一、第二、第四和第五图像对。 SR准确率仅为33.3%。 类似地,SAR-SIFT 的 NCM 也很小,分别为 6 和 8。 尽管SAR-SIFT重新定义了梯度的概念以适应SAR图像匹配任务,但重新定义的梯度对NRD更加敏感。 此外,SAR-SIFT 使用多尺度 Harris 检测器进行特征检测。 检测器通常获取的特征点较少,并且无法获取某些图像上的任何关键点。 例如,图12(b)中Google地图上SAR-SIFT检测到的特征点数量为0; 因此,NCM 必须为 0。LSS 在所有这六个图像对上均失败。 PIFD 仅在第二个图像对上成功匹配。 相比之下,所提出的 RIFT 算法在所有这六个图像对上都成功匹配,其 SR 准确率为 100%。 RIFT的NCM较大,分别为41、368、335、66、230和93。RIFT的平均NCM约为SIFT的7.8倍。
RIFT在具有NRD的图像对上的匹配性能远远优于当前流行的特征匹配方法。 主要原因有两个:(1)RIFT使用PC图代替图像强度进行特征检测,同时考虑特征重复率和特征个数,为后续匹配奠定基础。 (2)RIFT采用log-Gabor卷积序列构造MIM代替梯度图进行特征描述。 MIM对NRD具有很好的鲁棒性,从而保证了特征向量的准确性。 图13显示了RIFT的更多结果。

图 13. 所提出的 RIFT 的更多结果。 为了更好的可视化,显示的匹配项不超过 100 个。
2)定量比较:图14是NCM度量的定量结果,其中图14(a)∼图14(a)~图14(b) 图14(f)显示了三种比较方法在六个多模态数据集上的结果。 如图所示,SIFT 由于其对光照变化的抵抗力,在光学数据集和昼夜数据集上比其他 4 个数据集表现更好。 在光学数据集中,图像之间的成像机制差异比其他四个数据集要小,并且匹配相对容易。 昼夜数据集本质上也是一个光学数据集。 不同之处在于昼夜数据集的光照条件更加复杂。 SIFT 在深度光学数据集上的表现最差。 SR准确率为零,未获得正确的匹配。 原因可能如下:(1)SIFT使用梯度信息进行特征描述。 梯度可以在一定程度上反映图像的结构信息(边缘信息)。 然而,在深度图或视差图中,边缘结构相对较弱。 (2) SIFT直接根据强度检测特征点。 提取的特征点数量较少,且分布较差(特别是深度图和视差图,如图1所示),导致匹配性能较差。 在大多数成功匹配的图像对中,SIFT 的 NCM 都非常小(小于 50)。 在某些图像中,只有少数正确匹配的点。 SAR-SIFT的性能与SIFT算法相似,在光学-光学数据集、SAR-光学数据集和昼夜数据集上的性能优于其他4个数据集。 如上所述,光学数据集和昼夜数据集的图像对之间的成像机制差异相对较小。 由于SAR-SIFT算法是专门为SAR图像匹配而设计的,并且重新定义了梯度概念,因此它可能更适合SAR-光学数据集。 SAR-SIFT 在红外光学数据集和地图光学数据集上表现最差,几乎完全失败。 红外光学数据集的辐射特性差异较大,大多数物体的辐射特性完全相反。 如图9(b)所示,光学图像中的黑色物体在红外图像中呈现白色。 因此,重新定义的梯度可能对这种逆差更敏感。 如前所述,多尺度Harris探测器难以提取地图光学数据集地图上的特征点,这将不可避免地导致匹配失败。 在大多数成功匹配的图像对中,SAR-SIFT 的 NCM 也非常小。 然而,在少数图像对上,例如 SAR-光学数据集的图像对 9,SAR-SIFT 获得的 NCM 甚至比所提出的 RIFT 还要大。 一般来说,SAR-SIFT的匹配性能极不稳定。 LSS 在红外光学数据集上的表现比深度光学和地图光学数据集要好得多。 PIFD 在深度光学和地图光学数据集上完全失败。 相比之下,所提出的 RIFT 成功匹配了六个数据集的所有图像对,并且大多数图像对上的 NCM 远大于 50。 RIFT的匹配性能非常稳定和鲁棒,几乎不受辐射畸变类型的影响。 RIFT 远远优于其他方法。

图 14. NCM 指标的比较。 (a) 光学-光学。 (b) 红外光学。 © SAR 光学。 (d) 深度光学。 (e) 地图光学。 (f) 昼夜。
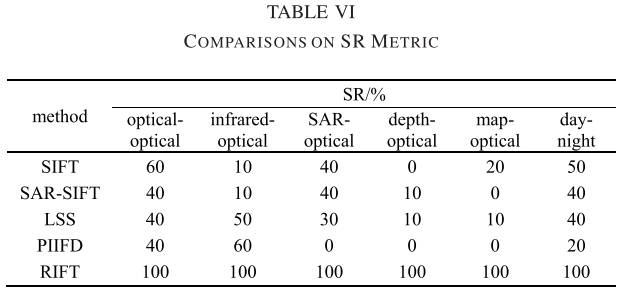
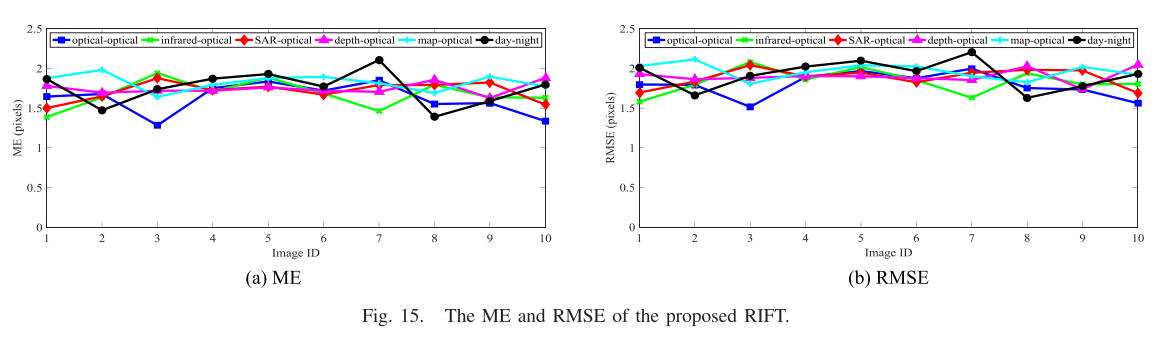
表 6 总结了六种方法在每个数据集上的匹配 SR。 如图所示,SIFT在光学数据集上的SR最高,为60%; SAR-SIFT在光学-光学、SAR-光学、昼夜数据集上的SR均为40%; LSS 和 PIFD 在红外光学数据集上均实现了最高 SR,分别为 50% 和 60%; 并且所提出的 RIFT 在所有数据集上的 SR 均为 100%。 SIFT、SAR-SIFT、LSS、PIIFD 和 RIFT 在所有六个数据集上的平均 SR 分别为 30%、23.3%、30%、20% 和 100%。 与 SIFT 和 LSS 相比,所提出的 RIFT 提高了 70%。 图 15 绘制了每个图像对上所提出的 RIFT 的平均 ME 和 RMSE。 由于其他方法的SR精度不够,因此没有计算其相应的ME和RMSE。 如图所示,RIFT 的 ME 和 RMSE 在 1 像素到 2.5 像素之间。 造成这些误差的原因有很多,比如地面真实几何模型估计误差、估计几何模型误差、特征点定位误差等。 表 7 报告了每个数据集上所提出的 RIFT 的 NCM、ME 和 RMSE。 从表中可以看出,RIFT的NCM比较大,而且非常稳定,都在100左右; 匹配精度高,ME约为1.75像素,RMSE约为1.9像素。 如前所述,RIFT 不受辐射畸变类型的影响。 所有 60 个图像对的平均 NCM、ME 和 RMSE 分别为 119.3、1.72 像素和 1.88 像素。
总结上述定性和定量实验结果,我们可以得出以下结论:所提出的算法是专门针对NRD问题设计的,包括特征检测和特征描述。 因此,所提出的算法具有很好的抗NRD能力,并且受辐射畸变类型的影响不大。 所提出的方法在所有六个数据集上都实现了非常好的 NCM 和匹配精度。 RIFT的匹配性能远远优于当前经典的特征匹配方法。 所提出的RIFT是一种具有旋转不变性、适用于多种多模态图像的特征匹配算法。
4.6 运行时间和限制
表 7 报告了每种比较方法在全部 60 个图像对上的平均运行时间,该时间是在配备 Intel i7-8550U @ 1.8GHz CPU、8 GB RAM 的笔记本电脑上计算的。 SIFT和LSS是用C++实现的,而其他是用Matlab实现的。 RIFT+表示没有旋转不变性的RIFT。 RIFT*处理基于并行计算的旋转不变性阶段。
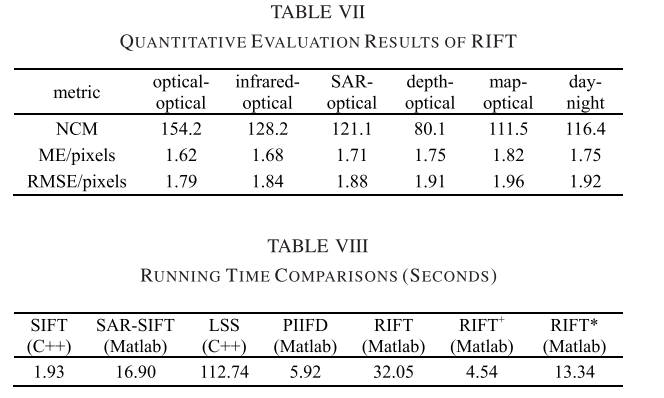
可以看出,RIFT的运行时间约为SAR-SIFT的2倍,PIIFD的5倍。 计算复杂度是 RIFT 的局限性之一。 比较 RIFT 和 RIFT+,我们发现 RIFT 中旋转不变性阶段的复杂度最高。 幸运的是,如果旋转先验已知,则可以通过在 RIFT 中设置标志参数轻松禁用旋转不变性阶段。 此外,旋转不变性阶段非常适合并行计算,并且可以轻松实现。 如图所示,RIFT仅花费 RIFT 运行时间的三分之一。 如果我们用C++重写RIFT,运行速度可以提高一个数量级。
RIFT 并不构建用于特征检测和描述的尺度空间。 因此,它对大尺度和视点变化很敏感。 为了解决这个问题,我们可以先建立一个类似于SIFT的高斯尺度空间; 然后,在最大矩图上应用精心设计的特征检测器,例如统一能力检测器[31],并在 MIM 上使用自适应分箱直方图技术[34],以实现对几何变化的鲁棒性。 如前所述,本文仅关注特征匹配中的NRD问题。 我们将在通用特征匹配框架中实施这些策略,以实现对几何和辐射变化的鲁棒性。
5 总结
在本文中,我们提出了一种辐射变化不敏感的特征匹配方法,称为 RIFT。 该方法具有旋转不变性,适用于多种多模态图像。 我们首先介绍了PC的概念。 RIFT的最初动机源于PC具有良好的辐射鲁棒性。 在分析和总结现有方法的缺点后,我们描述了 RIFT 的细节。 在特征检测中,我们基于PC图获得角点特征和边缘特征,同时考虑特征数量和重复率。 我们提出了用MIM代替梯度来进行特征描述,它对NRD有很好的鲁棒性。 我们还分析了旋转对MIM值的内在影响,并通过构造多个MIM实现了旋转不变。 在实验中,我们进行了定性和定量比较,以验证RIFT的可靠性和优越性。 我们还分析了 RIFT 的局限性。
6 代码
6.1 相位一致性matlab代码 phasecong3.m
phasecong3.m相位一致性计算的完整代码
1 | |
好的,让我们逐行解释这段 MATLAB 代码:
1 | |
这是函数的声明,它接受一个可变数量的输入参数,并返回多个输出参数。
1 | |
这一行使用checkargs函数来解析输入参数并设置默认值。
1 | |
这里定义了一个微小的常量epsilon,用于避免除以零。然后计算输入图像的大小,并对图像进行二维傅里叶变换。
1 | |
这一段创建了一些用于存储计算结果的变量,如卷积结果EO、相位一致性PC、协方差矩阵covx2、covy2和covxy,以及用于累积总能量的矩阵EnergyV。
1 | |
这里初始化了一个用于存储相位一致性总和的矩阵pcSum。
1 | |
这是一条注释,说明下面的代码段是用于加速滤波器构建的预处理步骤。
1 | |
这里根据图像尺寸设置了一个正态化的X轴范围。
1 | |
这里根据图像尺寸设置了一个正态化的Y轴范围。
1 | |
这里创建了网格坐标x和y,并计算了每个像素点的极坐标半径和角度。
1 | |
这里对半径和角度进行了象限移位,以便在滤波器构建时,将0频率放在图像的角落处。
1 | |
这里计算了正弦和余弦值,并清除了不再需要的变量。
1 | |
这段注释说明了滤波器的构建方式,即径向和角向组件相乘得到最终的滤波器。
1 | |
这段代码构建了滤波器的径向部分,使用对数 Gabor 滤波器进行滤波器构建。
1 | |
这段注释说明了滤波器的角向部分是如何计算的。
1 | |
这里初始化了用于存储角向和的矩阵。
1 | |
这里是角向分量的计算部分,对每个方向计算角度差,然后利用高斯函数计算角度分布。
这段代码是用来计算在图像处理中,如Gabor滤波器或方向性分析中,每个方向的频率响应的。下面是这段代码的逐行解释:
for o = 1:norient:这是一个循环,从1到norient,其中norient是预设的方向的数量。angl = (o-1)*pi/norient;:计算每个方向的角度。这里将圆周按norient等分,每一部分对应一个方向的角度。ds = sintheta * cos(angl) - costheta * sin(angl);:计算角度差的正弦部分。这里sintheta和costheta是基于频率空间坐标的正弦和余弦值。该公式实际上是旋转坐标系的公式的一部分,用于计算给定方向与当前像素点方向的差异。dc = costheta * cos(angl) + sintheta * sin(angl);:计算角度差的余弦部分。与ds的计算类似,这也是旋转坐标系的另一部分。dtheta = abs(atan2(ds,dc));:使用atan2函数计算两个方向之间的绝对角度差。atan2函数可以返回给定的正弦值和余弦值的角度,范围在-π到π之间,使用绝对值来获取正值。spread = exp((-dtheta.^2) / (2 * thetaSigma^2));:根据角度差计算方向性分量的权重,这里使用的是高斯函数来确定角度差的影响,thetaSigma是控制方向选择性敏感度的参数。sumAn = sumAn + spread;:将当前方向的权重加到总和中,sumAn用于累加所有方向权重的和。sumAsqr = sumAsqr + spread.^2;:此行将当前方向权重的平方加到另一个总和中,sumAsqr用于累加权重平方的和,可能用于后续的规范化处理或分析。sumAn = max(sumAn,epsilon);和sumAsqr = max(sumAsqr,epsilon);:这两行防止除零错误,通过确保sumAn和sumAsqr不会低于一个非常小的正数epsilon。结合方向滤波器公式来解释这段代码:
方向角的计算:
这里 (o) 是当前方向索引,() 是总的方向数。此公式计算每个方向滤波器的理想中心方向 ()。坐标的旋转:
这里分别是频率分量的正弦和余弦值,用于计算旋转后的正弦差和余弦差。这两个差值表征了频率分量方向与滤波器方向之间的角度差异。
角度差的绝对值:
使用atan2函数计算从 (dc) 和 (ds) 到其角度的反正切,结果是两个方向之间的角度差,范围在 。应用高斯函数:
这里控制高斯“钟形”曲线的宽度,即方向选择性。当角度差 接近零时(即频率分量的方向与滤波器方向接近时),高斯函数值较高,反之则较低。这种方法使得方向滤波器可以针对特定的方向有更高的响应,从而有效地提取或增强图像中该方向的特征。通过调整 ,可以控制方向滤波器的方向敏感度,使其在实际应用中更加灵活。
但是!!!在RIFT代码中构建方向滤波器是使用的是余弦调制函数,也就是
1 | |
当构建方向滤波函数时,我们的目标是设计一个函数,它在特定方向上具有高响应,并且在其他方向上具有较低的响应。这个函数通常被设计为在频率域中定义,以便通过傅里叶变换应用到图像上。下面我们来比较余弦调制函数和高斯函数两种形式:
- 余弦调制函数(Cosine Modulated):
余弦调制函数的一般形式为:
其中 是指滤波函数与给定方向之间的角度差。这个函数以 0 度方向为中心,对于与给定方向完全对齐的位置,它的值为 1,而在与给定方向垂直的位置,它的值为 0。这种形式是基于余弦函数的周期性特性,它提供了一种简单而有效的方法来实现方向选择性。
- 高斯函数(Gaussian):
高斯函数的一般形式为:
其中是控制滤波函数在方向上宽度的参数。这个函数基于高斯分布,它在方向上具有连续的变化,响应随着角度差的增加而指数级衰减。相比余弦调制函数,高斯函数在方向上的过渡更加平滑,能够提供更细致的方向选择性。
这两种形式之间的关系可以通过参数选择来建立。例如,当余弦调制函数中的角度差足够小时,余弦调制函数的形状与高斯函数是相似的。然而,余弦调制函数通常更简单,计算效率更高,因此在实际应用中经常被使用。
1 | |
这段代码是用来处理每个尺度下的滤波操作的。在多尺度分析中,滤波器会根据不同尺度对图像进行平滑或锐化,以便在不同的频率范围内检测图像的特征。
具体解释如下:
for s = 1:nscale:对于每个尺度,执行以下操作。filter = logGabor{s} .* spread;:将径向和角向成分相乘以获取滤波器。这里使用之前计算得到的 log-Gabor 滤波器和角度的分布函数spread,这个滤波器用于在特定尺度和方向上对图像进行滤波。EO{s,o} = ifft2(imagefft .* filter);:将图像的傅里叶变换与滤波器的频谱相乘,并通过逆傅里叶变换得到滤波后的图像。这里EO存储了滤波后的图像结果,其中s表示尺度,o表示方向。An = abs(EO{s,o});:计算滤波后图像的振幅响应。这个振幅响应表示了滤波器对图像在特定尺度和方向上的响应程度。即,sumAn_ThisOrient = sumAn_ThisOrient + An;:累加每个尺度下的振幅响应,用于后续估计噪声特征。if s == 1:当处理到最小的尺度时(即s == 1),估计滤波器响应的噪声特征。这里使用中值或众数来估计噪声的 Rayleigh 参数tau,以描述滤波器响应的分布。if noiseMethod == -1:如果选择使用中值来估计噪声统计信息,则通过计算振幅响应的中值来估计 Rayleigh 参数tau(,不同的地方写法不一样)。中值是指一组数据中处于中间位置的数值,用于描述数据的中心位置。if noiseMethod == -2:如果选择使用众数来估计噪声统计信息,则通过计算振幅响应的众数来估计 Rayleigh 参数tau。众数是指一组数据中出现次数最多的数值,用于描述数据的集中趋势。tau = median(sumAn_ThisOrient(:))/sqrt(log(4));:使用中值来估计 Rayleigh 参数tau,并对结果进行修正。这里的sumAn_ThisOrient(:)表示将sumAn_ThisOrient矩阵展平为一维数组,然后计算其中位数。Rayleigh 分布的参数tau与中值之间存在一定的关系,即,以使其更好地描述数据的 Rayleigh 分布特征。tau = rayleighmode(sumAn_ThisOrient(:));:使用众数来估计 Rayleigh 参数tau。rayleighmode函数用于计算给定数据的 Rayleigh 分布的众数。maxAn = max(maxAn,An);:记录每个尺度下振幅响应的最大值,这个值用于确定频率分布的加权。通过以上操作,每个尺度和方向下的图像都会经过相应的滤波器处理,得到相应的滤波后图像和振幅响应。
1 | |
这段代码执行以下公式:

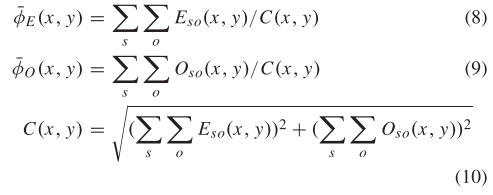
1 | |
噪声阈值估计:
- 如果
noiseMethod大于等于零,说明使用了固定的噪声阈值T。- 否则,通过估计每个滤波器响应的噪声效应的总和来计算一个总体噪声参数
totalTau。这是通过估计每个尺度上的响应的总和,然后使用几何级数来计算的。意会一下,尺度是成平方改变的,tau是最小尺度的估计噪声,所以尺度升高,估计噪声成指数改变。- 使用 Rayleigh 分布的特性估计噪声的平均值
EstNoiseEnergyMean和标准差EstNoiseEnergySigma。- 最终的噪声阈值
T是基于EstNoiseEnergyMean和EstNoiseEnergySigma以及参数k计算的。这个阈值用于软阈值滤波以减少噪声的影响。
1 | |
比起上面的公式,这段代码更像是在计算下式:
- 应用噪声阈值:
- 将计算得到的噪声阈值
T从能量Energy中减去,以减少噪声的影响。- 计算频率加权:
- 计算频率分布的宽度
width,通过将每个点上滤波器响应振幅的总和除以该点上的最大振幅来完成。这个宽度指标惩罚了特别窄的频率分布。如果只有一个非零分量,宽度值为 0;如果所有分量都相等,宽度值为 1。
- 这种计算的意义在于衡量图像中频率分布的多样性。在这个计算中,我们通过对每个点上的滤波器响应振幅求和,然后将该总和除以每个点上的最大振幅。这样做的目的是获取一个指标,该指标表示了图像中不同频率成分的相对强度,以及这些成分之间的差异程度。如果图像中只有一个频率成分,则频率分布的宽度会较小;而如果图像包含多个频率成分,则频率分布的宽度会较大。因此,通过计算频率分布的宽度,可以帮助我们理解图像中频率信息的丰富程度。宽度越大,权重越趋近于1。
- 计算用于该方向的 Sigmoid 权重函数
weight。该函数惩罚了频率分布特别窄的情况,公式中的cutOff和g是预先定义的参数。- 应用频率加权并计算相位一致性:
- 将加权能量
Energy乘以频率加权weight,然后除以总的滤波器响应振幅sumAn_ThisOrient。这个步骤得到了相位一致性(Phase Congruency)PC{o},代表了在该方向上的相位一致性度量。pcSum是PC{o}的累加值,用于计算相位一致性的总和。- 构建协方差数据:
- 通过使用相位一致性
PC{o}和角度angl来计算每个点的协方差数据,以获取图像中每个点的特征方向和特征相位类型。
1 | |
计算以下公式:
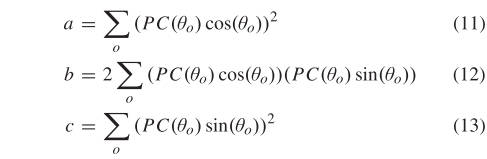
1 | |
计算以下公式:
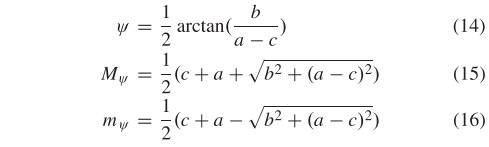
covx2 = covx2/(norient/2)的目的是为了归一化
1 | |
这段不太懂,应该是在计算图像的特征主方向。但是为什么要使用虚部的cos分量和sin分量?而且是基于滤波方向theta进行拆分,这样有什么意义?
可能会用到这张图进行理解:
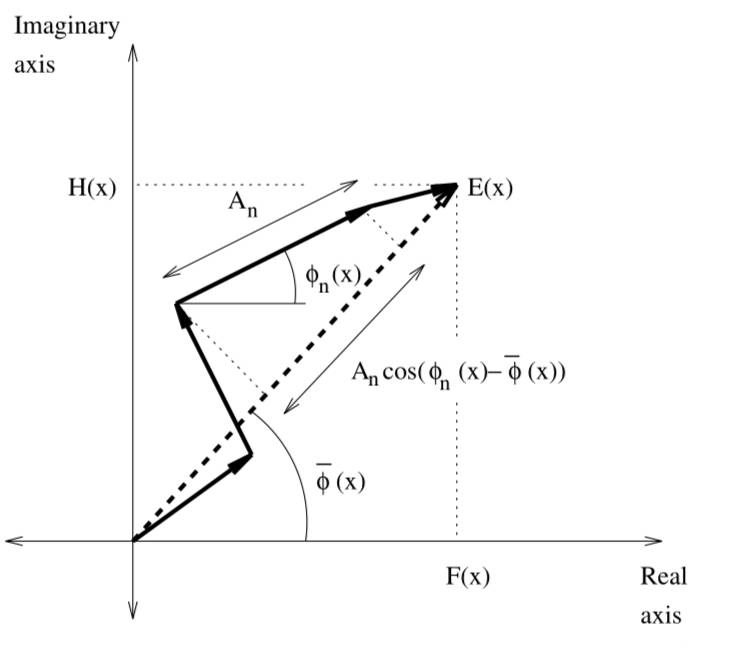
1 | |
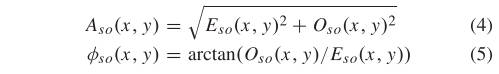
图像中每一点的局部加权平均相位角。