SRIF：多模态图像匹配，尺度不变算法和开放数据集

Multimodal image matching: A scale-invariant algorithm and an open dataset

SRIF：多模态图像匹配，尺度不变算法和开放数据集

Multimodal image matching: A scale-invariant algorithm and an open dataset (sciencedirectassets.com)

Multimodal image matching: A scale-invariant algorithm and an open dataset - ScienceDirect

摘要：

多模态图像匹配是信息融合、变化检测和基于图像的导航的核心基础。然而，多模态图像可能同时存在严重的非线性辐射失真(nonlinear radiation distortion，NRD)和复杂的几何差异，这对现有的方法提出了很大的挑战。尽管基于深度学习的方法在图像匹配方面显示出潜力，但它们主要集中在同源图像或单一类型的多模态图像上，如光学合成孔径雷达(SAR)。主要障碍之一是缺乏不同类型的多模态图像的公共数据。本文在多模态图像匹配领域做出了两大贡献:首先，我们收集了光学、光学-红外、光学- sar、光学-深度、光学-地图和夜间6种典型图像类型，构建了1200对的多模态图像数据集;该数据集在图像类别、特征类、分辨率、几何变化等方面具有良好的多样性。其次，我们提出了一种尺度和旋转不变特征变换(scale and rotation invariant feature transform，SRIF)方法，该方法在不依赖于数据特征的情况下获得了良好的匹配性能。这是我们的SRIF相对于深度学习方法的优势之一。SRIF通过将FAST关键点投影到一个简单的金字塔尺度空间中来获得关键点的尺度，这是基于研究在小尺度变化因子下带/不带尺度空间的方法具有相似的性能。与传统的高斯尺度空间相比，该策略大大降低了复杂度。SRIF还提出了一种类似sift的局部强度二值变换(LIBT)用于特征描述，可以极大地增强多模态图像内部的结构信息。在这1200对图像上进行的大量实验表明，我们的SRIF在很大程度上优于目前最先进的技术，包括RIFT, comfsm, LNIFT和MS-HLMO。创建的数据集和SRIF的代码都将在https://github.com/LJY-RS/SRIF上公开提供。

关键词:图像匹配、特征描述符、数据集、sar光学、多模态图像

1 引言

图像匹配在遥感和摄影测量领域有着重要的作用。这是图像融合等视觉理解和解释的基本问题(Ma et al.， 2019;Li et al.， 2022a)，变化检测(Tewkesbury et al.， 2015;Parente等人，2021)，以及图像定位和导航(mr - artal等人，2015)。然而，由于高层遥感应用的复杂性，单模态数据的信息丰富度不足。需要综合利用不同模态的数据，实现优势互补，从而提高图像理解的准确性和可靠性。幸运的是，随着传感器技术的快速发展，可见光相机、红外相机、合成孔径雷达(SAR)、激光器等成像设备不断涌现，为对地观测提供了多种数据源。因此，如何有效整合多传感器、多分辨率、多时相数据并进行深入分析已成为研究热点，而多模态图像匹配是急需解决的核心问题之一(Sui et al.， 2022)。

多模态图像匹配一般是指光学sar、光学深度等不同成像机制的多传感器图像之间的匹配(Li et al.， 2020a)。图像之间存在严重的非线性辐射差异(nrd)和复杂的几何差异(如尺度、旋转和视角变化)。这些差异使得配对成为一项具有挑战性的任务。近年来，人们为解决这一问题做了很多努力，并提出了许多多模态匹配算法。这些方法可以分为两类，即基于区域的方法(例如，定向相位一致性直方图(HOPC) Ye et al.(2017)和定向梯度通道特征(CFOG) Ye et al.(2019))和基于特征的方法(例如，辐射变化不敏感特征变换(RIFT) Li et al. (2020a)和局部归一化图像特征变换(LNIFT) Li et al. (2022b))。然而，这些方法主要集中在多模态图像的nrd上，对尺度变化等复杂的几何方差比较敏感。虽然共发生滤波空间匹配(comfsm) (Yao et al.， 2022)和局部主方向多尺度直方图(MS-HLMO) (Gao et al.， 2022)声称实现了旋转和尺度不变性，但在实验中，这两种类型的几何变化并没有同时发生在同一图像对上。

由于深度学习技术在计算机视觉领域的巨大成功，基于学习的方法在图像匹配任务中也显示出其潜力。例如，HardNet (Mishchuk等人，2017)和SuperPoint (DeTone等人，2018)在同源图像上实现了比传统手工制作方法更高的匹配性能。然而，这些方法受到泛化能力的限制，不能直接应用于多模态图像。Siamese CNN在光学sar匹配任务上显示出潜力(Zhang et al.， 2020;周等人，2021)。然而，它们是基于区域的匹配方法，而不是基于特征的匹配方法。此外，它们不能应用于其他类型的多模态图像，如光学深度、光学地图和夜间图像。阻碍深度学习技术在多模态匹配中成功应用的一个重要因素是缺乏不同类型多模态图像的公开数据。目前每个公开可用的数据集通常只包含一种类型的多模态图像，例如光学sar数据集(Huang et al.， 2021;Xiang et al.， 2020)和光学红外数据集(Brown and sstrunk, 2011;Jia等人，2021)。

为了促进多模态图像匹配，特别是基于学习的图像匹配技术的发展，我们创建并开放了包含光学-光学、光学-红外、光学- sar、光学-深度、光学-地图和夜间六种典型图像类型的多模态图像数据集。该数据集包含由三种不同类型的成像平台(包括航空、卫星和近距离)捕获的总共1200对图像。这些图像包含丰富的特征集(例如，建筑物，山脉，农田，湖泊等)，分辨率范围从0.04米到30米。此外，在这些图像中加入了不同的几何变化(旋转和尺度)，并进行了Ground Truth 变换。

我们还提出了一种多模态图像匹配的尺度和旋转不变特征变换(SRIF)方法。首先，通过实验研究了不同方法(带/不带尺度空间的方法)对小尺度变化因子的敏感性。基于有/无尺度空间的方法在小尺度变化因子下具有相似的性能，我们提出了一种简单的实现尺度不变性的策略。我们通过将关键点投影到一个简单的金字塔尺度空间中来获得关键点的尺度，这大大降低了复杂度。然后，我们提出了一种局部强度二值变换(LIBT)来增强多模态图像内部的结构信息，使特征描述符具有良好的可分辨性。我们将我们的SRIF与七个基线和最先进的方法在1200对图像上进行比较。结果表明，SRIF在很大程度上优于它们。

我们的贡献总结如下:

• 我们创建了一个开放的多模态图像数据集，包含1200对图像，涵盖六种典型类型的图像。
• 我们观察到，在小尺度变化因子下，有尺度空间和没有尺度空间的方法具有相似的性能。在此基础上，我们提出了一种基于投影的金字塔尺度空间构建策略，与传统的高斯尺度空间相比，该策略大大降低了复杂度。
• 我们提出了一种新的局部强度二值变换(LIBT)用于结构特征图的生成，可以在很大程度上增强多模态图像内部的结构信息。LIBT优于当前最先进的方法，如局部归一化图像(LNI)变换(Li et al.， 2022b)。
• 基于投影的金字塔尺度空间和LIBT，提出了一种多模态图像匹配的尺度和旋转不变特征变换(SRIF)方法。

2 相关工作

多模态图像匹配方法通常分为两类，即基于区域的匹配(也称为模板匹配或补丁匹配)和特征匹配(Li et al.， 2020a;Bas和Ok, 2021年;Mohammadi et al.， 2022)。每个类别都可以进一步细分为手工制作方法和基于学习的方法。

2.1 基于区域的方法

基于区域的匹配通常是基于滑动窗口策略，通过计算模板图像的相似度来找到模板图像在参考图像中的最优位置。

手工制作:手工制作方法最重要的事情之一是定义相似性度量。差分平方和(SSD)、互相关(cross-correlation)、归一化互相关(normalized cross-correlation)和互信息(mutual information)是常用的度量方法，其中互信息及其变体对nld具有更强的鲁棒性，被广泛应用于多模态图像匹配(Viola and Wells III, 1997;Liang et al.， 2013;Öfverstedt等人，2022b)。除了在空间域中的测量，相位相关方法通过傅里叶变换计算频域的相似性(Foroosh et al.， 2002)，这也被证明对非均匀照明变化具有鲁棒性。为了提高傅里叶变换方法的性能，有几种方法首先在傅里叶相关之前将原始图像转换到特征空间，如HOPC (Ye等人，2017)、改进的相位一致性模型(Xiang等人，2020)、CFOG (Ye等人，2019)和角度加权定向梯度(AWOG) (Fan等人，2021)。

基于学习的:这些方法从大量数据中自动学习高级信息，而无需手动提取特征。考虑到深度学习强大的特征提取能力，一些方法仅利用深度神经网络(DNN)获取特征，然后应用传统的相似性度量来搜索最佳匹配(Zhang et al.， 2020;Zhou et al.， 2021;Fang等人，2021)。相比之下，一些方法以端到端方式进行匹配，计算两个补丁之间的相似分数(Zhang等人，2019;Merkle等人，2017;Hughes et al.， 2018)。最近，有几种直接回归转换参数进行配准的方法，一般包括转换预测DNN、空间配准网络和反向传播DNN的优化器(Zhao et al.， 2021;Ye et al.， 2022)。基于学习的方法的局限性在于它们依赖于各种各样的训练数据集，并且需要大量的计算资源(Xiang et al.， 2021)。

基于区域的匹配通常对几何变换很敏感。虽然一些方法已经实现了基于变换优化器的旋转和尺度不变性(Öfverstedt等人，2022a,b)，但它们对局部极值敏感，计算复杂度高。

2.2 基于特征的方法

基于特征的匹配一般包括关键点检测、关键点描述和特征向量匹配三个主要阶段。首先，通过特征检测器(例如加速段测试(FAST)的特征(Rosten and Drummond, 2006)、Harris检测器(Harris et al.， 1988)、SuperPoint (DeTone et al.， 2018)等)提取具有高重复性的关键点，如角点。然后通过描述符(例如尺度不变特征变换(SIFT) (Lowe, 2004)、RIFT (Li et al.， 2020a, 2023)、HardNet (Mishchuk et al.， 2017)等)将这些关键点编码为特征向量，从而使特征具有更好的可区分性。最后，建立两个特征集之间的一对一匹配关系，并通过鲁棒估计技术或匹配策略(例如随机样本一致性(RANSAC)族)去除异常值(Fischler and Bolles, 1981;Li et al.， 2017)，稳健估计器(Li et al.， 2021a,b, 2020b, 2016, 2023b)， SuperGlue (Sarlin et al.， 2020)等)。

手工制作:传统的同源图像匹配方法已经取得了巨大的成功，并成为许多商业软件的标准方法，如SIFT (Lowe, 2004)， SURF (Bay et al.， 2008)， ORB (Rublee et al.， 2011)。然而，多模态图像的nrd对这些方法提出了很大的挑战。为解决这个问题已经作出了许多努力。例如，局部自相似描述子(LSS)及其变体提高了对光照差异的鲁棒性(Shechtman and Irani, 2007;Sedaghat and Mohammadi, 2019;Xiong et al.， 2021);为视网膜图像匹配设计了部分强度不变特征描述子(PIIFD) (Chen等，2010);位置尺度方向SIFT (Ma et al.， 2016)、方向图直方图(Fu et al.， 2018)和LGHD (Aguilera et al.， 2015)适用于多光谱图像匹配;提出了改进SIFT (Fan et al.， 2012)、optical-SAR SIFT (OS-SIFT) (Xiang et al.， 2018)和log-Gabor方向直方图的旋转不变振幅(RIALGH) (Yu et al.， 2021)来解决光学- sar匹配问题。然而，这些方法通常只适用于特定的图像类型，并不适用于其他类型的多模态图像，因此它们不具有通用性。最近，Li等人(2020a)提出了一种通用的多模态特征匹配方法，称为RIFT，它在不同类型的图像上都取得了很好的性能。几种变体通过增加尺度空间阶段、基于区域的精细配准步骤或修改最大索引图来改进RIFT (Cui et al.， 2020;Fan et al.， 2022;Yao et al.， 2022;Gao等人，2022)。此外，LNIFT在空间域中提出了局部图像变换，以实现接近实时的处理性能(Li et al.， 2022b)。然而，这些方法主要集中在NRDs上，而对复杂几何差异的鲁棒性尚未得到充分评价。

基于学习的特征匹配:基于学习的特征匹配在同源图像匹配方面取得了很大进展，如学习不变特征变换(LNIFT) (Yi等，2016)、HardNet (Mishchuk等，2017)、SuperPoint (DeTone等，2018)、D2-Net (Dusmanu等，2019)、LoFTR (Sun等，2021)等。对于多模态图像，Hughes等人(2020)开发了一种用于光学sar配准的三级卷积神经网络框架;Quan等人(2022)提出了一种自蒸馏特征学习网络，称为SDNet。但是，每种方法只能适用于一种特定的图像类型。如上所述，主要障碍是缺乏公共数据。

本文通过SRIF算法研究多模态图像的辐射和几何差异，并收集不同类型多模态图像的开放数据集，以促进基于学习的匹配的发展。

3 多模态图像数据集

如前所述，阻碍深度学习技术在多模态匹配中成功应用的一个重要因素是缺乏不同类型多模态图像的公开数据。在这里，我们收集并创建了一个包含光学-光学、光学-红外、光学- sar、光学-深度、光学-地图和夜间6种典型图像类型的多模态图像数据集，并向社会开放。希望能促进多模态图像匹配的发展。

3.1 光学-光学

我们使用WHU建筑数据集(Ji et al.， 2018)来生成我们的光学数据集，该数据集由一组覆盖新西兰基督城的预注册多时相航空图像组成。由于这些图像是在2012年和2016年拍摄的，因此两张匹配的图像之间的物体，纹理和红色发生了巨大变化。我们发现预注册不是很准确。因此，我们使用一种从粗到精的策略，即LNIFT + CFOG，来细化配准。然后将这些图像裁剪成512 × 512像素的子图像。我们随机生成一个旋转角度a∈[0◦，90◦]和比例因子𝑠∈[0.5,2]的ground-truth变换。将此变换应用于目标图像以获得我们的Optical-Optical数据集。

3.2 光学-红外

我们基于Ye et al.(2022)制作了光学红外数据集，其中原始图像来自覆盖成都平原及其周围丘陵和山脉的Landsat-8卫星图像。除了波段差异(光学为波段2，红外为波段5)外，该数据集还存在时间差异，因为光学图像是在2020年捕获的，而红外图像是在2021年获取的。利用几何校正技术对光学图像和红外图像进行精确对准。对于每一对，我们对目标图像进行随机旋转变换，即以目标图像的中点为旋转中心，逆时针旋转a∈[0◦，90◦]。

3.3 光学-SAR

光学SAR数据集是在LNIFT数据集2的基础上建立的，其中SAR图像由高分三号SAR卫星获取，光学图像由谷歌地球获取。该数据集涵盖了15个城市，包括北京、雷恩、奥马哈、德瓦卡等。由于每对图像之间已经存在旋转变化，因此我们只在每对图像中添加一个随机比例因子𝑠∈[0.5,2]，就可以得到最终的Optical-SAR数据集。

3.4 光学-深度

室内DIML/CVL RGB-D (Cho et al.， 2021)数据集用于生成我们的光学深度数据集，该数据集由微软Kinect v2摄像头获取。韩国的影像采集场景主要包括办公室、卧室、商场、展览中心等。与光学-红外数据集相同，我们还为目标图像添加了一个角度为a∈[0◦，90◦]的随机旋转。

3.5 光学-地图

该数据集由Ye et al.(2022)收集，该数据集来自谷歌地图服务。地点在东京，对象特征主要是建筑和街道。我们还使用了LNIFT + CFOG的策略来优化注册。然后，将图像调整为400 × 400像素，以获得最终的数据集。由于光学图像和地图之间的NRDs非常大，我们没有添加旋转和比例差异。因此，每个图像对的基真变换是一个单位矩阵。

3.6 夜间

夜间数据集是基于LLVIP (Jia et al.， 2021)数据集构建的，该数据集的图像由一台双目摄像机从26个不同的场景位置捕获。它不仅受到低光照条件(在夜间获取)的影响，还受到传感器差异(可见光相机和热红外相机)的影响。我们还为这个数据集添加了随机旋转。

表1总结了每个数据集的详细信息，包括数据集大小、图像大小、分辨率、几何变化、辐射变化等。图1显示了这六个数据集的示例数据。

图1。我们收集的多模态图像数据集的样本数据。我们的数据集由六种典型的多模态图像组成，包括光学-光学，光学-红外，光学- sar，光学-深度，光学-地图和夜间图像。

表1 我们多模态图像数据集的详细信息。

4 我们的SRIF

在详细描述我们的SRIF算法之前，我们首先介绍了SRIF使用的金字塔尺度空间策略，并为这种选择提供了实验支持。然后，给出了LIBT的定义和计算方法。因为这两点是所提出的SRIF与现有方法(如RIFT和LNIFT)的关键区别。

4.1 金字塔尺度空间

4.1.1 小尺度灵敏度

我们在我们的光学数据集上进行了实验，以揭示不同匹配方法对小尺度变化的敏感性。对于每一幅光学图像，我们将其自身作为参考图像，将其缩放后的图像作为目标图像来构建匹配对。比例因子设为{1,1.1,1.2,1.3}。也就是说，任何配对对都只有很小的尺度差异，不包括其他几何和辐射差异。我们选择SIFT、RIFT和LNIFT进行比较，其中SIFT有尺度空间，而其他的则没有。SIFT是应用最广泛的图像匹配算法。RIFT和LNIFT是最先进的sift类多模态图像匹配方法。这三种方法还提供对源代码的访问，从而促进实验过程。为了消除其他因素的影响，我们首先禁用它们的主导方向计算模块，并将主方向设置为0，即真实值;然后，我们移除最近邻距离比策略，因为它可能会丢弃真实匹配。我们使用正确匹配率(CMR)作为评估指标，它是正确匹配与总匹配的比率。结果如图2所示。

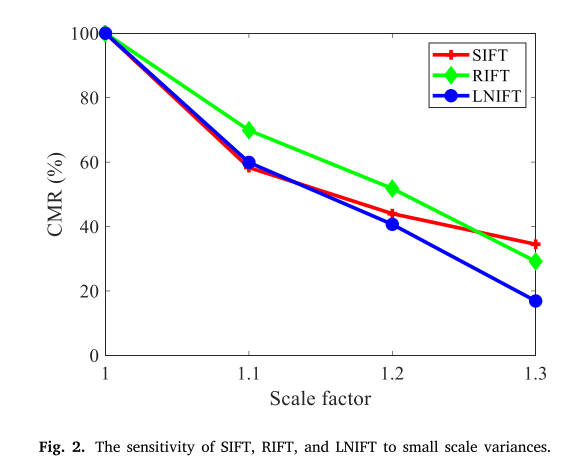
图2。SIFT, RIFT和LNIFT对小尺度方差的敏感性。

如图所示，当尺度在1到1.2之间变化时，SIFT的性能与LNIFT相当，而RIFT甚至优于SIFT。而当尺度差达到1.3时，RIFT和LNIFT的cmr均低于SIFT。因此，我们可以推断出一个结论，当尺度因子较小时，例如小于1.2，高斯尺度空间对匹配性能的改善非常有限。这也促使我们在没有多尺度高斯滤波的情况下通过下采样过程实现尺度不变性。只是下采样因子必须很小。实际上，这一结论与ORB (Rublee et al.， 2011)算法的尺度空间思想是一致的。此外，ORB算法的默认下采样因子也是1.2。我们基于投影的尺度空间与ORB的尺度空间的区别在于:第一，我们只构建目标图像的尺度空间，而保持参考图像不变。其次，我们只检测原始图像中的关键点，并将其投影到金字塔尺度空间的层上。在实验的基础上，给出了基于投影的尺度空间的合理性。虽然上述结论很重要，但理解结论背后的原因也很重要。例如，人工智能学者将深度学习的可解释性作为需要解决的重要问题之一。

4.1.2 基于投影的尺度空间

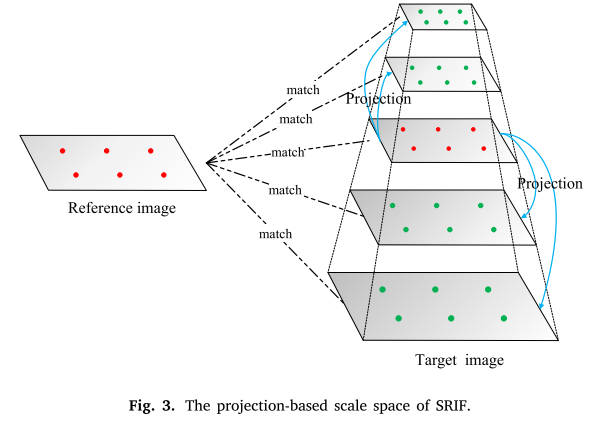
图3显示了我们的SRIF尺度不变性策略的细节。可以看出，SRIF只是为目标图像构建了金字塔尺度空间。金字塔层是通过同时对原始目标图像进行上采样和下采样得到的。在某种程度上，我们的方法与SI-PIIFD (Du et al.， 2018)、MS-PIIFD (Gao and Li, 2021)和MS-HLMO (Gao et al.， 2022)有一些相似之处，因为这些方法都是在高斯尺度空间框架的基础上进行改进的。与MS-PIIFD (Gao and Li, 2021)和MSHLMO (Gao et al, 2022)不同，我们省略了多尺度高斯滤波和差分运算步骤，而它们保留了全高斯尺度空间。虽然我们的方法和SI-PIIFD (Du et al.， 2018)都可以被认为是基于抽样的方法，但SI-PIIFD是基于加法运算的，而我们的方法是基于乘法运算的。此外，我们的方法只在目标图像上构建金字塔尺度空间，而这三种方法在参考图像和目标图像上都构建尺度空间。假设上/下采样操作次数为𝐾，尺度因子为𝑠，原始目标图像的图像尺寸为$[h,w]$，则金字塔共包含$2K+ 1$层，第i层($i\in\{1,2,...,2K+1\}$)的图像尺寸为$[w_i,h_i]$，

注意，第一层位于金字塔的底部。与ORB和SIFT不同的是，我们只检测原始目标图像中的关键点，并将这些关键点投影到金字塔层上，以获得多尺度关键点。对于下采样的金字塔层，我们只投射一些随机选择的特征。这样做的目的是为了避免特征之间的距离过小，导致用于特征描述的局部图像补丁之间存在较大的重叠，从而干扰后续的匹配过程。每层投影的关键点个数为;

其中，N是原始目标图像中关键点的个数。

为了适应我们的尺度空间策略，SRIF还修改了传统的最近邻匹配策略。传统的匹配策略首先将每个金字塔层上的特征点合并，得到总特征集。然后，对于参考图像中的一个特征，匹配策略在总集合中搜索最佳匹配。相反，我们不执行合并操作。我们首先在目标图像的金字塔尺度空间的每一层中搜索特征的最佳匹配，然后在这$2K+1$个特征中搜索最佳匹配作为该特征的对应。这种两级匹配策略可以有效地缩小匹配搜索空间。同时，由于缩小了搜索空间，匹配模糊的可能性也降低了。

4.2 局部强度二值变换(LIBT)

与传统匹配相比，多模态图像匹配的瓶颈在于严重的NRDs。虽然常用的强度和梯度信息对nrd很敏感，但幸运的是，大量研究表明，结构和形状特征是多模态图像匹配中非常重要的信息(Heinrich et al.， 2011;Li et al.， 2015;叶等人，2017,2019;Li et al.， 2020a)，因为它们以不同的方式保存，相对独立于辐射变化。因此，本文的核心思想是通过一些变换来增强图像中的结构信息，然后使用类似hog或类似sift的结构描述符来进行特征描述。

4.2.1 LIOT

最近，Shi等人(2022)提出了一种局部强度顺序变换(LIOT)来增强图像的结构。LIOT使用相对强度顺序来表征曲线结构的内在特性，而不依赖于绝对强度值。因此，它不仅增强了结构信息，而且具有良好的对比不变性。实验结果表明，LIOT可以有效地提高现有方法在视网膜血管分割和裂缝分割等任务中的性能。

图4。LIOT和LIBT图解。LIOT和LIBT都使用相对强度编码新图像，对对比度变化具有鲁棒性，可以有效增强结构信息。LIOT将图像转换为4通道图像，并且对旋转变化敏感。LIBT克服了LIOT的局限性，将图像转换为单通道归一化图像。(对于图例中有关颜色的解释，请参阅本文的网页版本。)

在这里，我们简要描述LIOT的基本思想。如图4(a)所示，对于图像$I$的一个像素$p$(图中红色像素)，LIOT将其强度$I(p)$与其相邻的8个像素$\{q_i^c|i-1,...,8\}$沿着四个方向中的一个进行比较，$c\in\{l,r,u,b\}$，其中$l,r,u,b$分别表示左、右、上、下。每个方向都可以生成一个8位的二维图像$\overline{I}^c$，其中强度$\overline{I}^c(p)$是根据$I(p)$和$I(q_i^c)$之间的强度顺序得到的二进制码计算得到的。计算公式为:

其中$\mathbb{I}[x]$是一个指示函数，如果事件x为真，则返回1，否则返回0。

可以看出，LIOT与方向高度相关，而旋转不变性是特征匹配的重要属性。此外，LIOT生成一个四通道图像，而特征描述只需要一个单通道图像。这使得LIOT无法用于图像匹配任务。

4.2.2 LIBT

为了解决上述两个问题，我们提出了LIOT的一种变体，称为LIBT。LIBT的图示如图4(b)所示。我们抛弃了LIOT中依赖于方向的像素顺序策略，直接将强度$I(p)$与其圆形区域内的所有像素$\Phi_p$进行比较，生成二进制代码。然后，将非零元素的比例计算为$\overline{I}(p)$的归一化强度值。显然，圆区域和非零元素的比例都是旋转不变的。因此，我们的LIBT公式为:

其中$|\Phi_p|$是该区域$\Phi_p$的总像素数

如上所述，我们希望通过LIBT增强结构信息，从而降低多模态图像匹配的难度。一般来说，图像之间的相似度与匹配难度成反比。这里的匹配难度主要是指NRDs的严重程度。因此，如果LIBT能够有效降低匹配难度，那么变换后的图像的相似度应该更高。为了验证这一结论，在我们收集的1200对图像的多模态数据集上进行了实验。在本实验中，我们使用ground-truth变换来准确地配准每对图像，以便更方便地进行图像相似性比较。我们使用习得的感知图像patch similarity (LPIPS) (Zhang et al.， 2018)作为评价指标，用于度量两幅图像之间的差异。LPIPS值越低，表示两幅图像越相似。LPIPS比传统方法更符合人类感知，如结构相似指数测度(SSIM) (Wang et al.， 2004)、相关系数、特征相似指数测度(FSIM) (Zhang et al.， 2011)等。

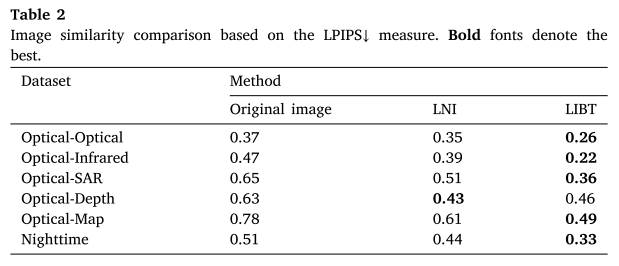
表2 基于LPIPS↓测度的图像相似性比较。粗体代表最好的字体。

表2报告了未进行任何变换的原始图像、局部归一化图像(LNI)变换(Li et al.， 2022b)和本文提出的LIBT变换的LPIPS结果。从结果中，我们可以得出以下结论:(1)LPIPS度量能够真实地反映图像之间的相似性。例如，OpticalSAR、Optical-Depth和Optical-Map的LPIPS值比其他类型的大，这与我们人类的感知非常一致，因为这三种类型的图像之间的差异明显大于其他类型。(2) LNI和我们的LIBT都可以提高原始图像的相似度，LIBT比LNI要好得多。可以看到，LIBT在6个数据集中的5个中达到了最好的结果，在光学深度数据集中只比LNI稍微差一点。原始图像、LNI和LIBT的平均LPIPS值分别为0.57、0.46和0.35。

4.3 SRIF的主要框架

我们的SRIF的主要框架如图5所示，其中也包含了特征检测、特征描述和匹配三个主要阶段。在本文中，我们只关注前两个阶段。

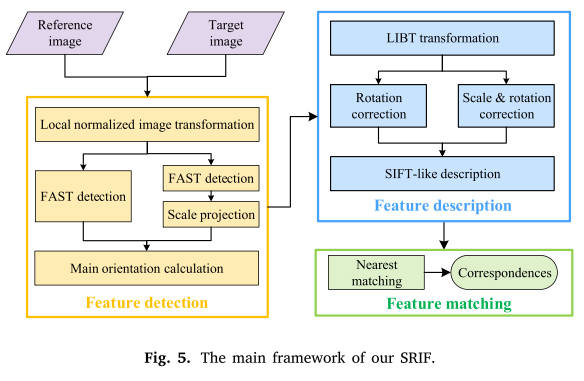
4.3.1 特征检测

我们首先基于提出的LIBT将原始图像转换为变换后的图像，并检测FAST特征。Li等人(2022b)指出，FAST特征容易聚集。因此，为了获得均匀分布的关键点，我们还使用自适应非极大抑制策略来抑制聚类特征。然后，我们将目标图像的特征投影到金字塔尺度空间中，以实现尺度不变性。可以看出，我们先检测特征点，然后进行尺度空间投影，这与传统方法的步骤完全相反。最后，采用与SIFT相同的方法实现旋转不变性。具体来说，我们使用梯度方向直方图技术获得直方图最大值和局部极值，并将所有大于最大值80%的局部极值作为特征的主方向。根据4.2.2节的实验结论，我们可以用LNI代替LIBT，在Optical-Depth数据集上获得更好的结果。

4.3.2 特性描述

同样，我们也对经过libt变换的图像执行特征描述。首先，SRIF计算LIBT图像的梯度映射，并将方向归一化为[0◦，180◦)，因为多模态图像通常具有相反的方向。然后对特征点对应的局部图像进行裁剪。参考补丁只需要旋转，而目标补丁需要同时旋转和缩放。所有局部补丁被调整为相同的大小，以方便后续的特征描述。然后，我们使用类似sift的描述符进行特征向量编码。描述符首先将一个含有$J\times J$像素的局部patch划分为若干个节点$N_{grid}\times N_{grid}$.

我们为每个网格计算一个$N_{bin}$-histogram，并获得总共个$N_{grid}\times N_{grid}$直方图。然后将这些直方图连接在一起，得到一个长度为:$N_{grid}\times N_{grid}\times N_{bin}$的特征向量，然后对其进行归一化以提高对光照变化的鲁棒性。实际上，我们的描述方法和LNIFT是一样的，只是用于描述的层不同。我们使用LIBT，而LNIFT使用LNI。因此，我们使用与LNIFT相同的参数，即:$N_{grid}=8,N_{bin}=4$

5 实验

在这里，我们在收集的1200对多模态数据集上对所提出的SRIF进行了综合评估。我们的SRIF与七个基线或最先进的算法进行了比较，即SIFT (Lowe, 2004)、OS-SIFT (Xiang等人，2018)、RIFT (Li等人，2020a)、3MRS (Fan等人，2022)、comfsm (Yao等人，2022)、LNIFT (Li等人，2022b)和MS-HLMO (Gao等人，2022)。实验中使用了每种方法的正式实现。为了公平比较，我们将特征的最大数量设置为5000，并对除了3MRS、comfsm和MS-HLMO之外的所有比较方法应用相同的匹配策略(使用蛮力搜索来建立一对一的对应关系，而不使用最近邻距离比(NNDR)测试)，因为3MRS、comfsm、而MS-HLMO只提供二进制代码，难以修改。表3总结了每个方法的参数设置、实现细节和不变性属性。

定量评价采用三个指标，即正确匹配数𝑛、均方根误差(RMSE)r和成功率$\gamma$。请注意，在评估所有方法之前，我们没有应用类似ransac的方法或局部几何约束来过滤离群值，因为我们的目标是评估局部描述符，而这些离群值去除方法可能会丢弃一些真正的内线。这三项措施的定义如下:

• 正确匹配数𝑛:一个映像对中正确对应的数目。如果Ground Truth 变换下对应的残差小于$\varepsilon$ ($\varepsilon$ = 3)，则接受其为正确值。

• 成功率$\gamma$:如果图像对的正确匹配数满足𝑛≥10，则认为图像对匹配成功，因为太小的𝑛会导致后续的模型拟合失败。

• RMSE 𝑟:假设$\{(x_i,y_i)\}_1^n$是图像对的正确对应关系，$𝑇(⋅)$表示其真值变换，则RMSE计算公式为:

  

  对于那些无法匹配的图像(𝑛< 10)，我们将它们的均方根误差设置为20像素。

5.1 定性评价

使用图1所示的每种类型的多模态图像的第一对进行比较。第一个图像对受到时间、尺度和旋转变化的影响;第二对具有波段和旋转差异;第三对受到严重的斑点噪声、尺度和旋转变化的影响;第四种在成像机制和旋转变化上有很大的不同;第五对的地图并不是真正的图像;最后一种受弱光条件、传感器差异和旋转变化的影响。图6显示了各算法的比较结果。

可以看出，SIFT和OS-SIFT只在Optical-Optical对上实现了成功匹配，但正确匹配的次数非常少。SIFT使用梯度进行描述，这已被证明对NRDs非常敏感。OS-SIFT是专为光学sar匹配而设计的，不适合其他类型的多模态图像，具有严重的NRDs。RIFT和LNIFT在没有尺度变化的图像对上表现良好，因为它们不能实现尺度不变性。3MRS的结果最差，即不能匹配所有对。3MRS使用一种从粗到精的配准策略，这对尺度或旋转变化都没有鲁棒性。因此，当图像对遭受较大的几何变化(如旋转、缩放、透视等)时，3MRS的性能非常差。comfsm和MS-HLMO仅在第一对上表现良好。虽然这些方法在一些数据集上取得了很好的结果，但它们在我们收集的数据集上表现不佳。一个可能的原因是我们的数据集更困难。例如，在他们的实验中，尺度和旋转的变化不会同时出现在同一图像对上。相比之下，我们的SRIF在所有图像对上都取得了最好的结果。我们的正确匹配数𝑛比RIFT和LNIFT等其他方法要大得多。

5.2 定量评价

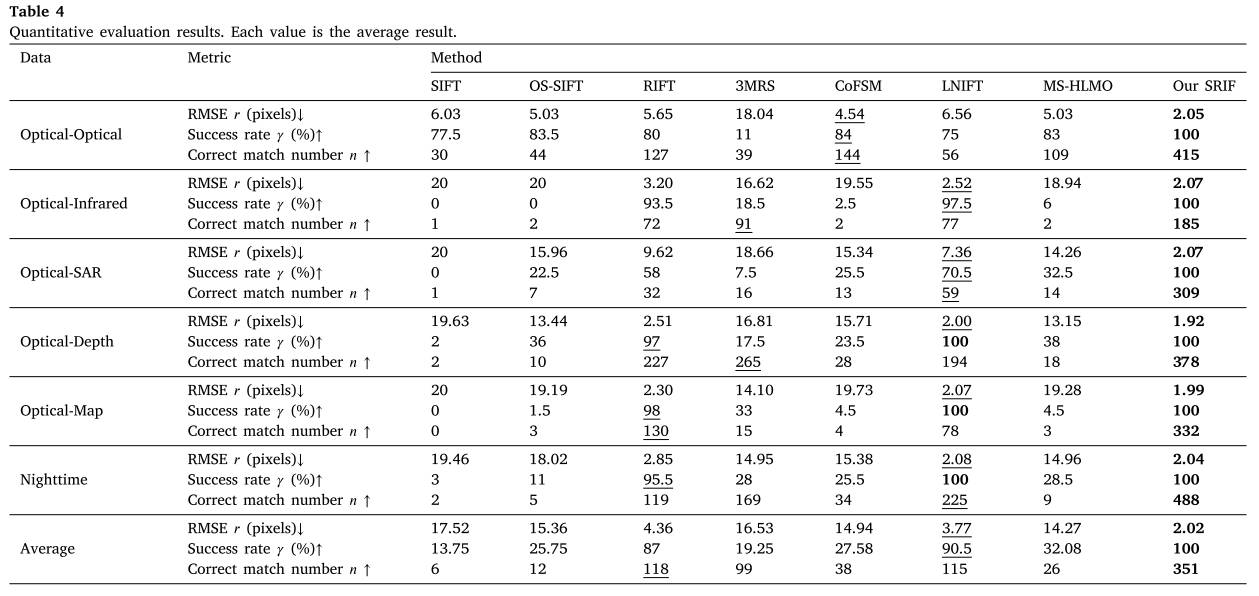
表4 定量评价结果。每个值都是平均结果。

定量结果如表4所示，包括正确匹配数𝑛(越高越好)、RMSE𝑟(越低越好)和成功率<s:2>(越高越好)。由图可知，SIFT只适用于nrd较少的光学图像。在其他类型的多模态数据集上，其成功率接近于0。这是可以预测的，因为SIFT算法通常用于同源图像匹配。OS-SIFT的性能略好于SIFT，因为它修改了梯度的计算，提高了对散斑噪声的鲁棒性。然而，它在光学-红外和光学-地图数据集上的性能很差，因为这些数据集的主要匹配困难不是散斑噪声。即使在SAR-Optical数据集上，OSSIFT的性能也远远不够好。主要原因是OS-SIFT不会衰减光学图像和SAR图像之间的nrd。3MRS在任何一个数据集上的成功率都不超过40%。原因是它没有考虑图像之间的旋转和尺度变化，而我们数据集中的大多数图像对都存在旋转方差或尺度变化。我们还观察到，尽管3MRS的成功率较低，但它的平均正确匹配数仍然很高。例如，它在光学红外和光深度方面排名第二。这是因为3MRS使用密集模板匹配方法来细化粗特征匹配结果。comfsm和MS-HLMO在OpticalOptical数据集上表现良好，在其他数据集上与OS-SIFT相当。comfsm和MS-HLMO的性能不理想可能是由于我们的数据集匹配难度高。在comfsm和MS-HLMO的原始论文中，它们只在小规模数据集上进行了测试，没有复杂的几何变化。在没有尺度变化的情况下，RIFT和LNIFT在数据集上取得了非常高的成功率(约90%)。即使在具有尺度差异的数据集(如光学sar数据集)上，它们的成功率仍然高于50%。如4.2.2节所示，虽然RIFT和LNIFT不构建尺度空间，但它们仍然具有一定的抵抗尺度变化的能力，特别是对于小尺度因子。在我们的数据集中，比例因子在0.5到2之间，这不是很大。我们的SIRF获得100%的成功率和超过300次的正确匹配。我们的SRIF之所以表现如此出色，主要有两个原因:首先，我们的方法实现了旋转和尺度不变性，因此可以处理复杂的几何差异;其次，我们提出了利用LIBT变换增强图像中的结构信息，从而大大降低了NRDs。LIBT优于LNI，这使得SRIF获得比LNIFT更好的匹配结果。

8种比较算法在6个数据集上的平均成功率分别为13.75%、25.75%、87%、19.25%、27.58%、90.5%、32.08%和100%。我们的SRIF与第二好的方法，即LNIFT相比，获得了10%的增长率。在正确匹配数𝑛方面，SIFT、OS-SIFT、RIFT、3MRS、comfsm、LNIFT、MS-HLMO和我们的SRIF的结果分别为6、12、118、99、38、115、26和351。我们的匹配正确率是RIFT和LNIFT的3倍，是comfsm和MS-HLMO的10倍左右。我们的RMSE在3像素的初始阈值下约为2像素。在光学深度、光学地图和夜间数据集上，它略好于LNIFT，在这些数据集上，LNIFT的成功率也为100%。这种匹配精度足以满足许多遥感应用。众所周知，基于模板的方法的匹配精度通常优于基于特征的方法。如果我们想在需要非常高几何精度的应用程序中使用它，可以应用基于模板的匹配算法(如CFOG)来进一步改进我们的结果。

5.3 消融研究

为了验证所提出的SRIF算法中关键新步骤的有效性，我们在我们的多模态图像数据集上进行了消融实验。本实验比较了五种不同的管道设置(BL、RI、SI分别代表基线、旋转不变性模块和尺度不变性模块):

• BL:从我们的SRIF算法中删除旋转不变性和比例不变性模块;
• BL+RI:仅从我们的SRIF算法中删除尺度不变性模块;
• BL+SI:仅从我们的SRIF算法中删除旋转不变性模块;
• BL‘+RI+SI:仅将SRIF算法中的LIBT替换为局部归一化图像(LNI)生成结构特征图;
• BL+RI+SI:提出的SRIF算法。

1200对图像的平均定量实验结果如表5所示。

如图所示，(1)将BL+RI(或BL+SI)与BL进行比较，我们可以看到旋转不变性模块和尺度不变性模块可以大大提高成功率和正确匹配数;(2)将BL+RI+SI(我们的SRIF)与BL*+RI+SI (SRIF_LNI)进行比较，我们可以看到LIBT比LNI可以生成更好的结构特征图。成功率提高了4.5个百分点，正确匹配次数提高了30%以上。

5.4 计算时间

通过实验比较了这些方法在光学深度数据集上的计算时间性能。将图像大小调整为256 × 256、512 × 512、768 × 768和1024 × 1024像素，生成四个不同图像大小的数据集。本实验在3.6 GHz, 8核，i9-10850K CPU, 64gb RAM的PC上进行，实验结果如表6所示。

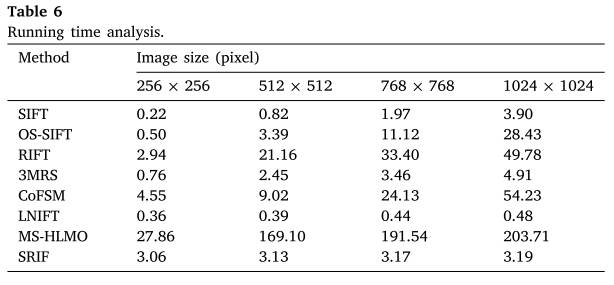
我们的SRIF的计算时间对图像大小的依赖性较小，因为与特征检测和描述相比，LIBT的计算复杂度非常低，这与LNIFT非常相似。实际上，SRIF和LNIFT的计算时间主要受特征数量的影响，但我们将其固定为5000，因此SRIF在不同大小的图像上的计算时间是相似的。从结果来看，当图像尺寸较大时，我们的SRIF比RIFT, comfsm和MS-HLMO运行效率高得多。例如，在512 × 512图像上，SRIF比RIFT快7倍，比comfsm快3倍，比MS-HLMO快53倍。它排名第四，仅比SIFT、3MRS和LNIFT慢。当图像大小为1024 × 1024时，SRIF分别比RIFT、comfsm和MS-HLMO快15倍、17倍和63倍，在8种方法中排名第二。

5.5 局限性

我们的SRIF的局限性主要体现在两个方面:

• 与LNIFT相比，SRIF的计算复杂度较高，不适合实时/近实时匹配任务。由于我们构建尺度空间的方式，在目标图像上投影后的特征数量很高。此外，𝐾= 3只能覆盖0.5到2之间的尺度变化。然而，当图像之间的尺度变化较大时，我们需要增加𝐾的值，但这也会增加投影特征的数量，进一步降低算法的效率。一种可能的解决方案是在减少尺度方差之前使用粗糙的地面样本分辨率或使用GPU实现加速。
• 正确匹配率较低，这是当前多模态特征匹配方法的普遍局限性。虽然我们的SRIF在上述实验中可以得到很多正确的对应，但它是基于提取大量的特征点，即在投影前提取了5000个特征点。事实上，我们的正确匹配率仍然很低，大多在10%以下。因此，在实践中，我们需要增加特征的数量来保证匹配性能，这将增加SRIF的计算复杂度。一种可能的解决方案是学习类libt或类lni图像，基于深度学习强大的特征提取能力提取多模态图像之间的共同特征。

6 结论

本文建立了光学-光学、光学-红外、光学- sar、光学-深度、光学-地图和夜间6种典型图像类型的多模态图像数据集，并向社会开放。该数据集共包含1200对图像对，在图像类别、特征类、分辨率、几何变化等方面具有良好的多样性。我们希望它能对多模态图像匹配，特别是基于学习的图像匹配技术的发展做出一点贡献。我们还提出了一种多模态特征匹配的尺度和旋转不变特征变换(SRIF)方法。在对小尺度灵敏度实验分析的基础上，提出了一种简单的尺度空间构建策略。为了增强多模态图像的结构信息以抵抗NRDs，我们提出了一种局部强度二值变换(LIBT)来进行特征描述，并基于LPIPS度量验证了其有效性。通过对比7种基线和最先进的算法在1200对图像上的表现，我们可以看到我们的SRIF在很大程度上优于它们，即我们的方法获得了10%的成功率，并且与第二好的方法相比，我们的方法获得了三倍的正确匹配。我们未来的工作将集中在基于学习的类libt图像生成和基于学习的特征描述。