GAMES202_高质量实时渲染

GAMES202_高质量实时渲染 Real-Time High Quality Rendering

GAMES202-高质量实时渲染_哔哩哔哩_bilibili

Real-Time：渲染速度达到30FPS，在VR/AR中需要到90FPS

High Quality：保证真实性，即物理上是近似正确的

Rendering：模拟一个虚拟的摄像机看到一个虚拟场景时，获得的信息。通过光线追踪，模拟光线弹射来实现。

课程包括四个部分：

• 阴影和环境
• 全局光照
• 基于物理的着色
• 实时光线追踪

Real-time rendering（RTR） = 快速且近似离线渲染+系统工程

0 基础知识回顾

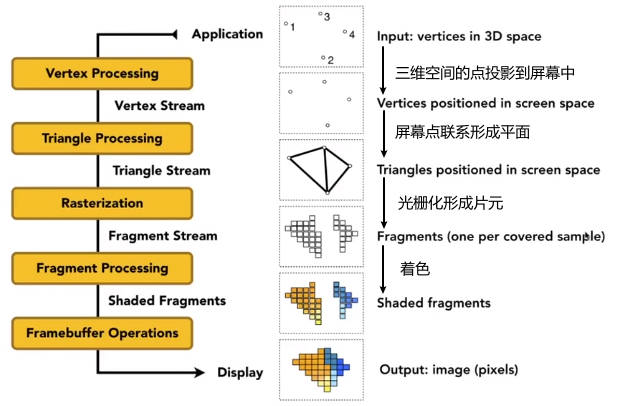
0.1 渲染管线

0.2 OpenGL概述

教程搜索LearnOpenGL

• OpenGL是一系列API，是在CPU端中负责安排GPU怎么执行
• OpenGL是跨平台，语言无所谓
• OpenGL的版本很碎片，新版本不一定好
• OpenGL是C语言风格
• OpenGL目前似乎不更新了，Vulkan可以看作是OpenGL的后续
• 理解OpenGL：画画
  • 摆放物体：目标物体的位置、属性 vertex buffer object(VBO)将物体的三角形顶点、法向量进行存储
  • 摆放画架：相机、视点的位置、属性 framebuffer帧缓冲器
  • 设置画布：成像平面 相同的 framebuffer可以渲染不同纹理的图像，换个“画布”就行
  • 在画布上作画：成像 shader
• 总结：状态机模型？
  • 定义 物体、相机、MVP等属性
  • 定义 framebuffer帧缓冲器、输入输出的纹理
  • 定义 物体的顶点、片元着色器
  • 将这些东西放入GPU中，进行渲染

0.3 Shading Languages （SL）

• HLSL（high level SL）-> DirectX（vertex+pixel）
• GLSL -> OpenGl（vertex+fragment）
• Shading Languages （SL）需要通过编译，才能在GPU中执行

0.3.1 Debugging Shaders

多年前，SL是非常难调试的。为什么？因为SL是在GPU中运行的，而GPU的多线程不能像CPU那样打断点来单步调试。

现在调试SL的方法有：

• Nsight Graphics：跨平台，但是仅限于NVIDIA GPU
• RenderDoc：跨平台，没有GPU限制
• 上述两种是否可以用在WebGL中？（待验证）
• RGB调试法：GPU不能直接打印变量值，那么就将变量值归一化为RGB值，并作为图片打印处理

0.4 渲染方程 Rendering Equation

渲染方程的常规描述：

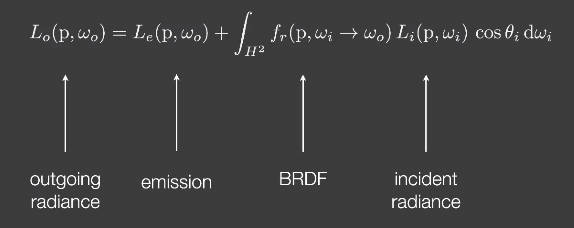
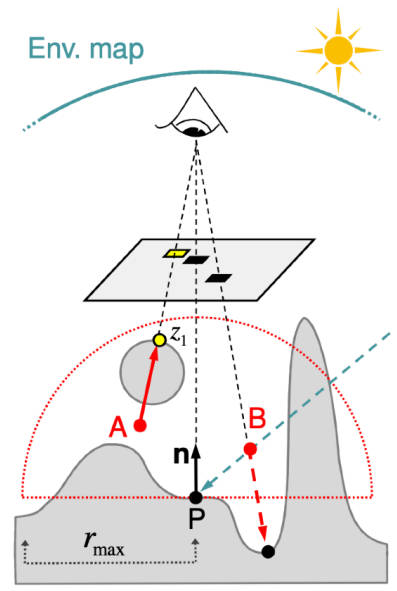
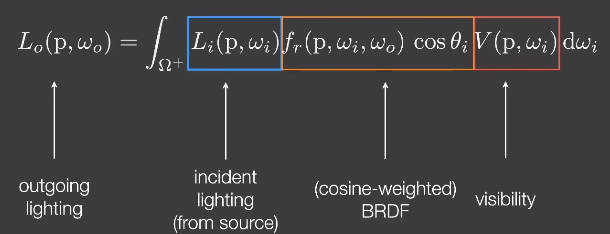
在实时渲染中，

• 表示从$w_i$方向去看点p的可见性（是否有遮挡）的变量$V(p,w_i)$被加入到公式中
• 这里的BRDF通常是将$\cos\theta_i$考虑在内，只与材质有关
• 这两个公式完全等价

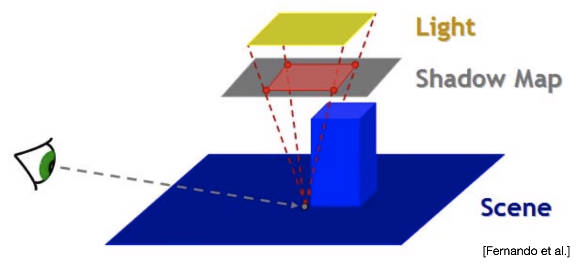
1 阴影映射 shadow mapping

核心思想：两阶段算法（点光源为例）

• 第一步：从光源打出光线，渲染与最近物体相交的深度，将深度作为纹理存储
• 第二步：从相机打出光线，真正开始渲染

特点：

• 不需要场景的几何信息
• 会造成自遮挡和错误识别、走样的问题

著名的shadow mapping方法：

• Basic shadowing technique even for early offline renderings, e.g., Toy Story

1.1 核心思想

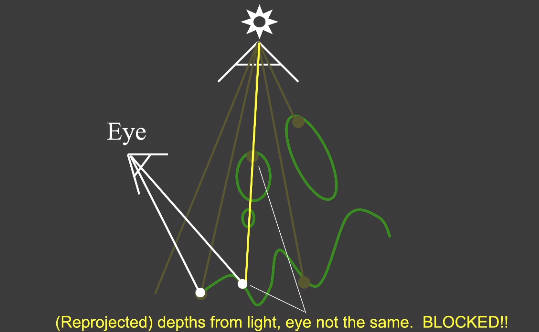
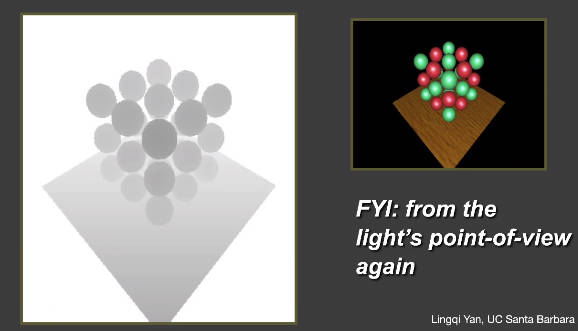
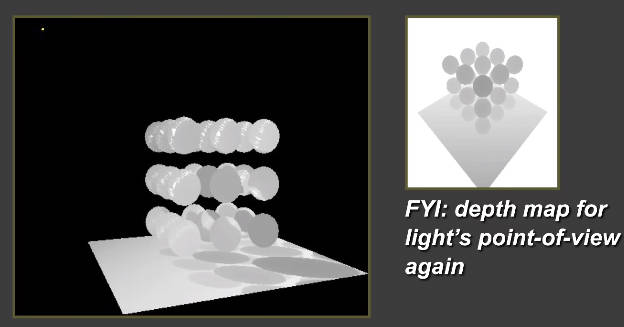
核心思想：两阶段算法（点光源为例）

• 第一步：从光源打出光线，渲染与最近物体相交的深度，将深度作为纹理存储
• 第二步：从相机打出光线，真正开始渲染

1.2 阴影映射存在的问题

1.2.1 自遮挡

下图中劳拉身旁不规则的阴影就是自遮挡现象。白色区域是光滑的地面，这些阴影原本不应该存在的。

怎么理解这些阴影？可以理解为原本光滑的平面变成了不规则隆起或则凹陷的沙丘，从而形成了阴影。

为什么会变成“沙丘”呢？因为深度信息是通过以光源作为视角获得的深度信息（纹理信息）。这些信息存储在depth-buffer缓冲器中，也就是一个数组。这会导致深度信息离散化，就像右图那样，原本是光滑的黑色平面，但是通过depth-buffer重构的确是红色表面。绿色部分就是隆起或则凹陷的程度，从而造成了阴影。可见，自遮挡的程度与光源的角度和离散化程度有关。

工业界普遍的解决方法就是：

既然因为离散化导致了绿色部分的深度差，那么设置一个阈值（bias），使得在深度差阈值内的值均不计算阴影。

但是这也导致本来该有阴影的地方变得没有阴影。

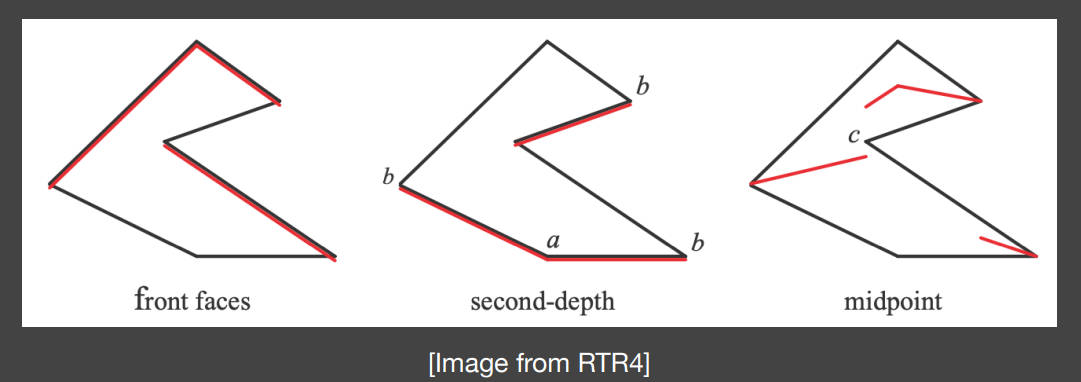
进一步改进的方法是使用Second-depth shadow mapping，也就是除了生成最浅深度信息外，还生成第二浅深度。然后将两个深度的中间值midpoint作为shadow mapping的depth-buffer。

这样做的好处是：

• 如果物体是平面的话，造成阴影的深度是在平面以下，所以阴影也在平面之下
• 如果物体是立体的话，虽然造成阴影的深度会改变，但是物体产生的阴影始终在物体之下，并且不会出现阴影与物体断开的情况

1.2.2 走样

depth-buffer是离散化的，因此在生成阴影时会出现锯齿

1.3 微积分预备知识 约等式

本节会涉及到经典微积分不等式

注意，在实时渲染RTR中，RTR不关心不等式，而是关心 近似相等

两个函数先乘再积分和先积分再乘：

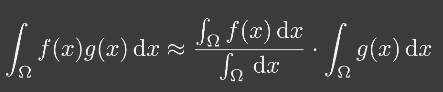
这个公式什么时候适用？满足一个条件就行：

• 当$g(x)$的支撑集（support）也就是$\int_\Omega$足够小的时候，也就是函数值不为零的积分区域
• 当$g(x)$足够光滑的时候

马上应用一下：

考虑这个近似公式的满足条件：

• 当$g(x)$的支撑集（support）也就是$\int_\Omega$足够小的时候
  • 什么时候$\int_\Omega$，也就是函数值不为零的积分区域足够小？足够小，小到只有一个单位方位角，也就是只有一束光。
  • 一束光是意味着什么？意味着点光源。
  • 也就是说，当光源是点光源（或者是硬阴影）的时候，公式适用
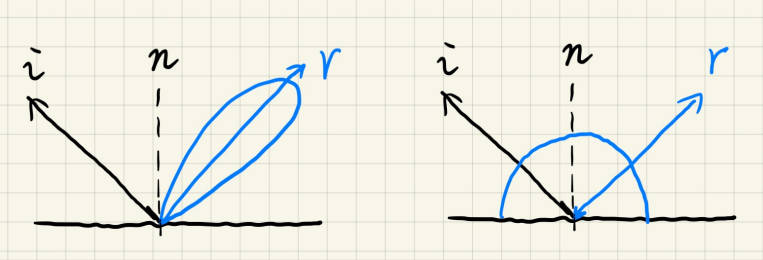
• 且当$g(x)$足够光滑的时候
  • 当光源是面光源的时候，$L_i$可以看作是光滑的，因为各个方位的照度区别不大
  • 当着色点的材质是diffuse的时候，它的BRDF就是光滑的，因为向各个方向发射的照度是均匀的

1.4 软阴影 PCSS

上述的shadow mapping方法获得的是硬阴影。但是软阴影才是shadow mapping追求的目标。

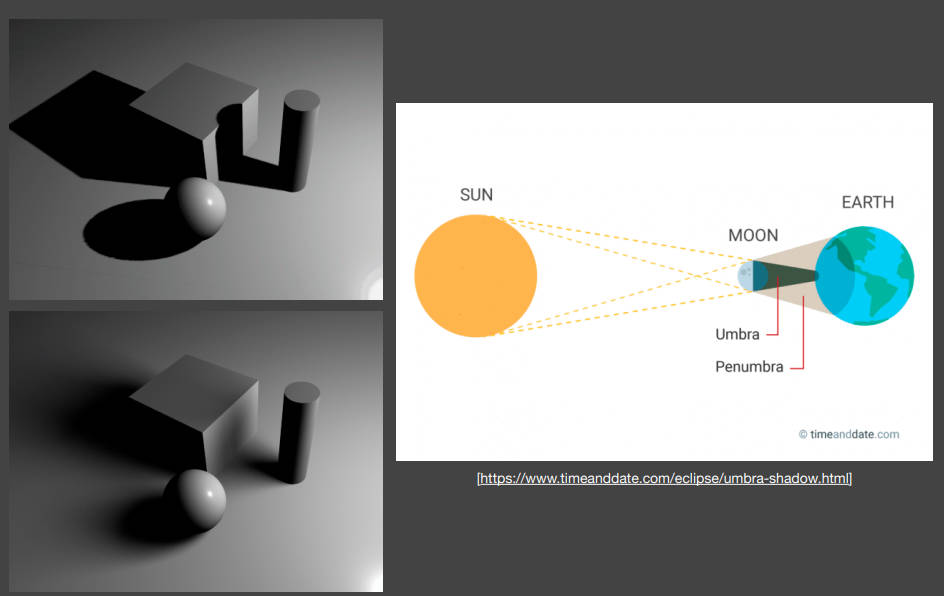
软阴影是怎么形成的？软阴影和硬阴影的区别在于没有明显的边界。这是因为在边界处返回去看光源，会发现光源是部分可见的。

1.4.1 百分比渐近滤波 Percentage Closer Filtering（PCF）

PCF简单来说就是做了个均值滤波。但是是在哪里进行的滤波？

不是在depth-buffer中，也不是在shadow mapping中，而是在visibility中进行。

visibility是什么？相机看过去的目标点是否会被遮挡，这会生成一个01矩阵，大小和相机的成像图像一致。这个就是visibility矩阵，对这个矩阵进行均值滤波，从而模糊阴影。

1.4.2 Percentage Closer Soft Shadows （PCSS）

一句话总结PCSS：自适应的调整PCF的滤波窗口大小

PCF是如何控制阴影的软硬程度？通过调整滤波器的窗口大小。越大，越模糊，也就越软。

但是这个窗口大小是人为设定的。这显然不够适应多种情况，有没有什么办法来自适应调整窗口大小。也就是说阴影的软硬程度和场景中的什么有关系？

PCSS给出的答案是光源距离阴影对应的物体的远近

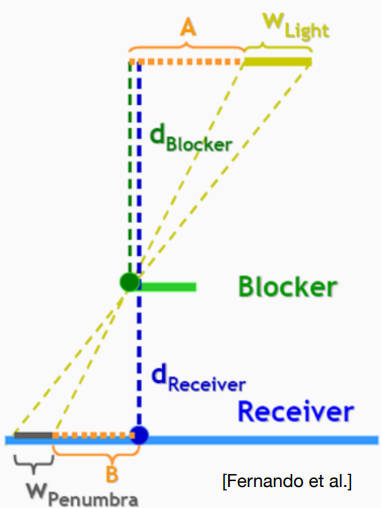
上图中灰色部分就是软阴影的区域，与光源形成了一个相似三角形。Blocker就是遮挡物。

如何理解？当光源是点光源的时候，黄色区域和灰色区域都是0。当光源越靠近Blocker的时候，灰色区域就越小。

因此，根据软阴影区域的大小来自适应的调整PCF的窗口大小，这就是PCSS的思想。

最后一个问题：

• Blocker是什么？不就是遮挡物吗？没错，上面的演示图中将Blocker视作平面。
• 但是在实际案例中，Blocker可以是各种各样的曲面。怎么办？求平均深度，把它近似为一个平面。因为阴影不用特别精确。
• 在多大的范围内求平均深度？简单方法就是用一个5X5的窗口来计算。另外一个启发式的方法：
  • 将目标点和面光源生成为一个视锥，Blocker在视锥内的截面大小视作窗口大小。
  • 

However，这样的计算方法的计算开销非常的大！！！

但是PCSS是现在最常用的方法，因此后续提出了许多加速方法。

1.4.3 方差软阴影映射 Variance Soft Shadow Mapping （VSSM）

前面提到，PCSS的计算开销非常大。接下来分析一下是哪里的计算量大：

• 第一步：寻找Blocker，计算Blocker的平均深度
• 第二步：根据Blocker的平均深度自适应调整PCF的窗口大小
• 第三步：计算PCF

计算量大在哪里？大在需要使用滤波器进行平均的步骤，也就是第一步和第三步。计算平均深度要用到均值滤波，计算PCF要用到均值滤波。简单来说就是在求均值时，计算量非常大。

计算量为什么大？因为对于每个像素（或者说每个元素），计算次数都是窗口面积大小。也就是$O(filter_{size}\times filter_{size}\times N)$。

VSSM就是针对性的解决这个问题。->求均值时，计算量大的问题

回顾一下PCF中的Visiblity矩阵是怎么计算的？是通过比较目标点的深度是否比光源的depth-buffer要浅。

Visiblity矩阵的均值滤波是什么？就是在目标点周围选定一个小的搜索区域一起进行比较，看看深度更浅的点所占的百分比是多少。进一步说，在PCSS中Blocker近似为平面，所以搜索区域对应的光源的depth-buffer是一个平均值t。因此，问题变为了目标点周围的一个搜索区域内，有多少点的深度要比t浅，也就是比t浅的点所占百分比是多少。

这样计算势必会遍历一遍搜索区域内所有的点，从而增加计算量。

VSSM不想对于每个目标点都要这样遍历一遍搜索区域。

VSSM将搜索区域内的点的深度分布视为正态分布

• 缺点：这种近似非常大胆，但是阴影映射也并不需要特别精确，所以只用通过正态分布函数大概知道百分比就够了
• 优点：搜索区域的深度视为正态分布，要计算正态分布中大于t的百分比，可以直接用累计分布函数表示，只需要知道正态分布的均值和方差

只需要均值和方差的好处是只需要遍历一遍所有的深度即可，而不是对每个搜索区域都要均值一下。

如何在一次遍历中知道任意矩形内的均值？使用积分图 Summed Area Tables

已知均值之后怎么求方差？公式：$Var(X)=E(X^2)-E^2(X)$，因此只需要遍历深度时，顺便将深度的平方存储下来，构建另一个积分图即可。

综上：VSSM利用正态分布近似和积分图，顺利将 “比t浅的点所占百分比是多少” 这个问题从$O(filter_{size}\times filter_{size}\times N)$的复杂度变为了$O(N)$，速度加快了数十倍。

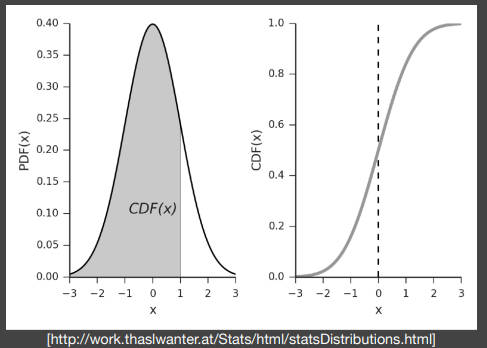
however，正态分布的累计分布函数没有解析解，只有数值解，也就是一个表格记录所有解的数值。在C++中叫error_function。

为了避免查表。VSSM引入了切比雪夫不等式：

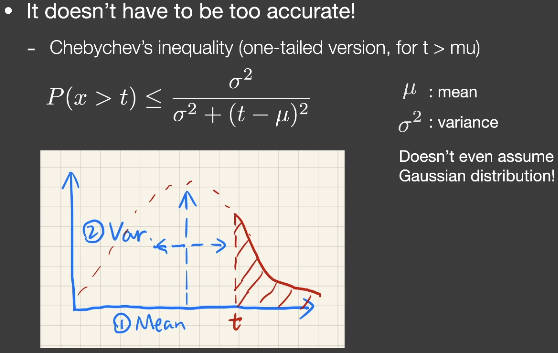
在实时渲染RTR中，不考虑不等式，而是考虑约等式。

切比雪夫不等式是说，知道一个分布的均值和方差（可以不是正态分布），那么这个分布中大于t的面积一定不大于上述公式。但是有一个条件，t必须在均值的右边。

虽然但是，人们仍然使用切比雪夫不等式来计算。

上述过程解决了第三步PCF的计算复杂度。但是怎么快速计算Blocker的平均深度仍然是个问题，因为Blocker是不规则的，没有办法直接用积分图来计算。像下图所示，蓝色的深度更浅，是遮挡物，它的边界不规则，所以不能用积分图。

考虑这样一件事：Blocker的平均深度 X Blocker的元素个数 + Non-blocker的平均深度 X Non-blocker的元素个数 = 整个区域的平均深度 X 整个区域的元素个数。这是一个显然的事情

将这件事写成下面这个公式。百分比就自然出来了。百分比出来，那么就可以用上面介绍的切比雪夫不等式进行计算了。

这里VSSM又做了一个假设，将Non-blocker的平均深度设为t。t是划分Blocker的阈值，也就可以理解为Blocker之下物体的平局深度。这个假设如何理解？因为被投影的物体大多是平面，或者说在一个小区域内可以近似为平面，所以假设还算合理。

综上：VSSM降低了PCSS中计算Blocker平均深度和PCF均值滤波的计算复杂度。通过正态分布、积分图和切比雪夫不等式。

VSSM在这个过程中提出了非常大胆的假设，并且有很多近似。

however，实时渲染结果的对与错，是由观看者来决定的，而非数值。

“看起来是对的，那就是对的”

再however，现在来看，人们对于VSSM和PCSS的使用度相当。SAT的构建速度相对较慢。

1.4.4 Moment Shadow Mapping

VSSM将搜索区域的深度分布假设为正态分布。

那么当深度分布与正态分布相差很大会怎么样呢？

会导致Visibility的均值滤波值出现与事实相差较大的结果。反应到阴影中就是过亮或者过暗。事实上，阴影如果过暗，对于人眼来说还可以接受。但是致命的是阴影会过亮。

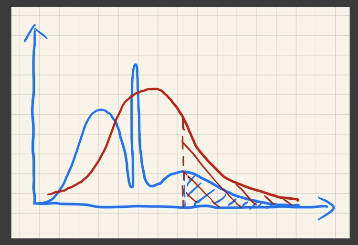
这个问题本质就是深度分布不满足正态分布的假设。

Moment Shadow Mapping的目的就是想办法使用更高阶的矩（moment）来表示深度分布。

矩是什么东西？简单的理解：以深度为例，记录深度的是一阶矩$x$，记录深度的平方是二阶矩$x^2$,记录深度的三次方是三阶矩$x^3$，等等。以这个角度来看，VSSM是使用的一阶矩和二阶矩来表示深度分布。

Moment Shadow Mapping是使用了更高阶的矩来表示。这有点像球谐函数、泰勒展开、多项式展开、过拟合的思想。

表示什么？数学结论表明，用前m阶的矩，可以表示一个具有$m/2$阶的阶跃函数。

阶跃函数有什么用？思考VSSM做出正态分布假设的目的是什么。VSSM是想通过正态分布假设，用正态分布的累积分布函数（CDF）来表示Visibility的百分比。累积分布函数（CDF）是一个从0到1单增的函数。从0到1单增，那是不是可以用阶跃函数来表示。也就是说用前m阶的矩来表示累积分布函数（CDF）。

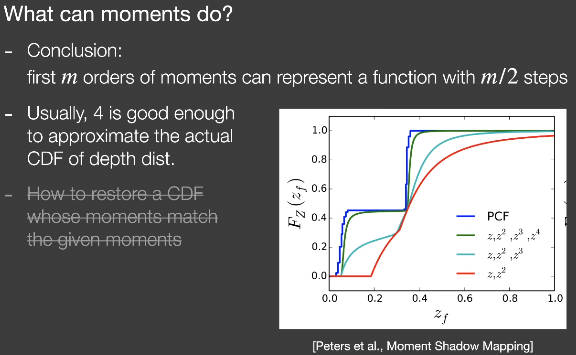
however，计算过程会非常复杂。

1.5 距离场软阴影 Distance field soft shadows

1.5.1 Distance Functions

想象一个黑色区域在一个白色区域向右平移，获得A和B两个图像。现在想要获得平移过程中处于A和B中间位置的图像。

简单的想法是直接做像素插值。但是这样做的结果是lerp(A,B)的图，也就是中间位置是灰色的，这显然不是想要的结果。

那么怎么做呢？定义两个Signed Distance Field（SDF，有向距离场）。令SDF中的元素表示该元素到边界处的距离，且左边的取为符号。对这两个SDF进行插值，再根据插值后的SDF反过来获得实际像素值。这样就获得了A和B的中间态。

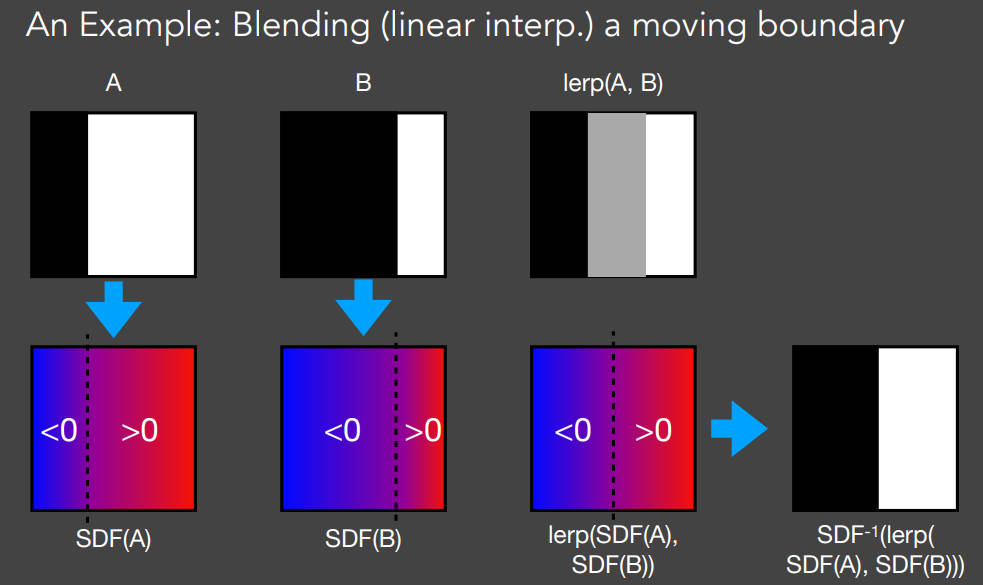
SDF与一个理论联系密切，Optimal Transport 最优传输。

SDF的相关应用：

• 融合，Blending。

• 光线行进算法 Ray Marching RayMarching入门 - 知乎 (zhihu.com)

  • 如何理解Ray Marching ？
  • 举个例子，打出一束光线，在光线的起始位置计算其SDF的值，也就是与物体相交的最小距离。以这个SDF的值的半径画一个圆，这个圆和物体只有一个交点。这时可以将这个SDF的值理解为安全距离，也就是光线从起始位置出发，随便往哪个方向走，只要走的长度在安全距离内，光线就不会与任何物体发生相交。
  • 因此我们获得了一个光线行进的方法，让光线每次沿着光线的方向行进一个安全距离，直到安全距离足够小或者行进的距离足够远。
  • 

• 软阴影

  • 将安全距离变为安全角度。像下图这样，光线的安全角度越小，说明光线被遮挡的越厉害，所以阴影越硬。
  • 
  • 
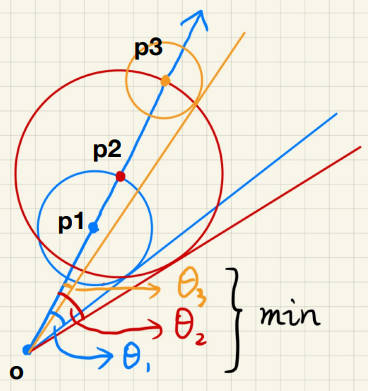
  • however，计算安全角度会使用反三角函数，这是在实时渲染中需要避免的情况。
  • 反三角函数的值应该是在[0,1]之间，并且这个安全角度不是非求不可。本质上是根据SDF和$|p-o|$的比值来衡量阴影的软硬。
  • 既然如此，使用$\min\{\cdot,1.0\}$来限定比值范围，然后使用k来调节比值的权重。从而实现和反三角函数差不多的效果。k越大，即使比值很小，也会被算成1，也就是安全角度为0，即阴影越硬。
  • 

SDF长什么样？（很深的方向，还待继续了解）不好贴纹理

2 实时环境映射 Real-time Environment Mapping

环境映射，就是假设环境光照是在任意方向都是无限远的。

现在给定一个环境光照，将一个物体放在场景中，不考虑遮挡（without shadows）。怎么对这个物体进行着色shading？

这种操作叫做Image-Based Lighting（IBL）

IBL操作是基于渲染方程。不考虑遮挡，也就是visibility全是1。

求解这个值，通用的解法是使用蒙特卡洛积分。也就是对光源和像素进行多次采样求平均。

但是在IBL中，光源是来自四面八方的，这对于光源采样来说，需要的采样量是非常大的。（however，现在GPU似乎可以逐渐解决这个任务）。排除GPU的性能逐渐提升来说，只要是采样，就很难应用到实时渲染中。另一方面，使用蒙特卡洛积分需要采样，而采样会引入噪声。

因此在IBL中要避免采样。

回顾第1.3节中介绍的约等式。注意这里的支撑集是对于$g(x)$来说的

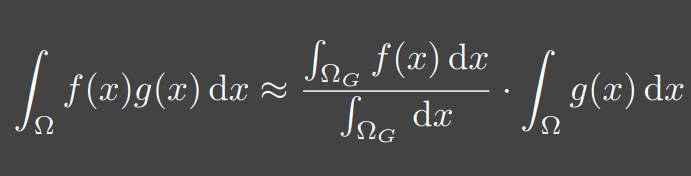
放到渲染方程中，会发现：

• 材料如果是glossy（镜面），BRDF的支撑集足够小
• 材料如果是diffuse（漫反射），BRDF足够光滑

所以渲染方程就可以写成约等式：

观察黄色框圈出来的部分。这是不是形似

$\frac{\sum f(x)*x}{\sum x}$

这可以理解为归一化，也可以是均值滤波，模糊化。

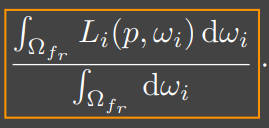
进一步的说，这个公式是在shade point的球面上以方位角作为滤波器的窗口进行均值滤波。

对于gloss的BRDF来说，它的支撑集只有一个小lobe（波瓣），左图蓝色区域，也就是一个小的方位角。这个公式计算的就是入射光在这个lobe上的均值滤波。

怎么求解这部分呢？对于蒙特卡洛积分来说，就是多次采样入射光，然后求平均。

怎么避免这样采样呢？预滤波（pre-filtered），既然都是均值滤波，先后有什么区别。先对整个半球的入射光进行不同程度（不同大小方位角）的滤波，这就像MIPMAP，不过不在预设方位角中，就三线性插值。这样就将多次采样求平均变成了，只采样lobe中心的光线，公式的值就变为以lobe的方位角大小进行的均值滤波，而这个值预先已经计算好了。

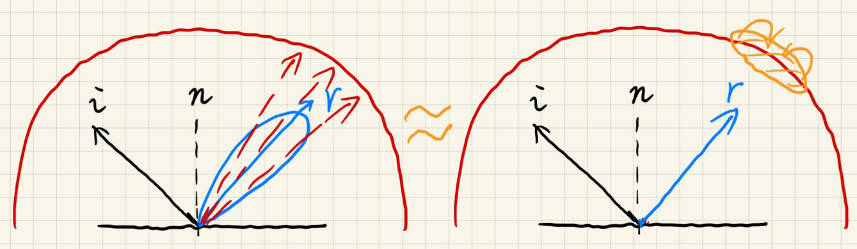
观察公式的第二部分：（淦，没懂。。

微表面模型(Microfacet Model) - 知乎 (zhihu.com)

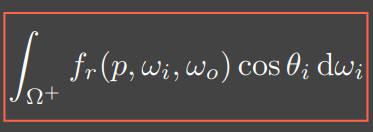
Split sum。。应用在虚幻引擎中

2.1 来自环境光的阴影

计算来自环境光的阴影是一件非常困难的事情，这可以从两个角度来看：

• 作为一个多光源问题：将环境光作为许多个光源，然后做shadow map。相当于每个光源都要做一遍shadow map。这会线性的增加计算量
• 作为一个采样问题：通过渲染方程来计算。然后使用Split sum的操作。但是因为是计算阴影，所以要考虑Visibility这个函数。Visibility不具有像BRDF在gloss或者diffuse的那两种特性（support小或者光滑），所以没有办法使用Split sum中的近似不等式。

那么怎么解决这个问题呢？

• 只计算贡献最多的光源。在户外的话，贡献最多的光源是太阳。这样计算量就降下来了。这在工业界是使用很广的方法。
• Imperfect shadow maps
• Light cuts -> offline rendering
• RTRT -> real-time ray tracing（可能是最后的解决方法
• Precomputed radiance transfer

2.2 预备知识

2.2.1 频率和卷积

• 两个函数相乘再对变量积分 等价于 卷积操作
• 什么是低频函数？光滑的函数，变化量小的函数就是低频函数
• 两个函数卷积得到函数的频率由两个函数中频率更低的函数的频率决定

2.2.2 基函数

一个函数可以由一系列基函数的线性组合来表示

2.3 实时环境光照 Real-time environment lighting & global illumination

2.3.1 球谐函数 Spherical Harmonics（SH）

怎么理解球谐函数？就像多项式展开、傅里叶展开。球谐函数在其中扮演的就是基函数的角色，用这些基函数来表示任意一个的球面函数。球谐函数的阶表示基函数的频率，也是类似多项式的次方数

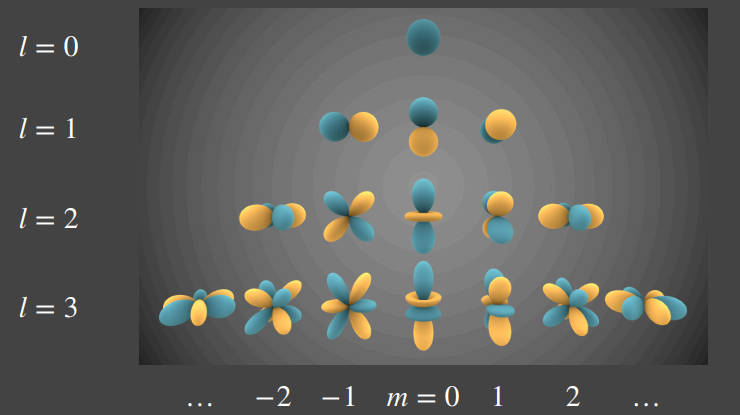
球谐函数的特性：

• 每个球谐函数基函数 $B_i(\omega)$可以由一个 Legendre 多项式表示

• 投影：原函数$f(\omega)$与任意一个基函数$B_i(\omega)$相乘再积分，这个过程叫做投影，也就是向基函数方向投影。获得的值就是$B_i(\omega)$进行线性组合表示原函数$f(\omega)$的系数

  • $c_i=\int_{\Omega}f(\omega)B_i(\omega)d\omega$

  • 怎么理解这个投影？类比三维向量向坐标轴进行投影，投影的结果也是一个数，这个数用于线性表示这个三维向量的系数。

• 球谐函数基函数互相之间正交，也就是投影之后值为0

• 球谐函数易于计算旋转后的结果

  • 一个球谐函数旋转，等效于其球谐基函数各自发生旋转。
  • 一个球谐基函数旋转后的函数，可以由其同阶的基函数的线性组合来表示
  • 因此，如果一个球谐函数发生旋转，可以用旋转后的球鞋基函数表示，旋转后的球谐基函数可以由其同阶球谐基函数的线性组合表示。线性组合怎么求？基函数本身是不会变的，所以线性组合也是不会变的，所以将每种角度的线性组合计算出来，然后存储成一张表就行了。

2.3.2 预滤波环境光 Prefiltered env. lightinh

再次回顾预滤波的作用： 预滤波 + 单次查询（采样）= 没有滤波 + 多次查询（采样）

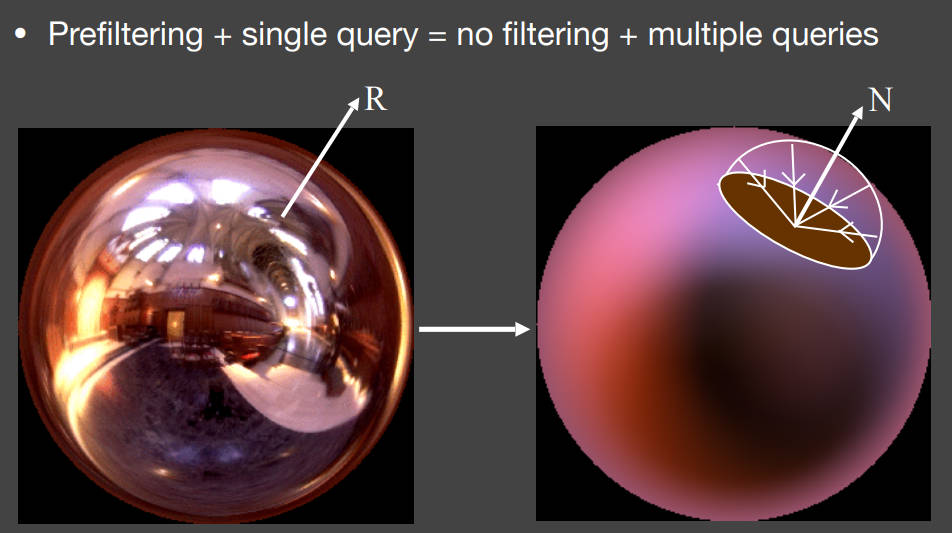
重新考虑一下环境光映射时的渲染方程：不考虑shadow，也就是visibility

这个方程中，入射光$L_i$和BRDF其实都是球面函数，这没什么好说的。

球面函数就可以用球谐函数来表示了。

用几阶的球谐函数来表示呢？

大师Ravi进行了实验（只是对Diffuse BRDF）。Diffuse BRDF应该是一个比较光滑的函数，光滑以为着低频，低频意味着使用低阶的球谐函数就可以表示了。

Ravi的实验结果也验证了这一点。他不断提高SH的阶数来表示一个相同的Diffuse BRDF。发现SH的系数在第三阶的时候就已经趋近于0了，后续阶数同样如此。

因此，Ravi指出用前三阶SH即可表示Diffuse BRDF。

再看这个计算形式，是不是两个函数相乘再积分？在第2.2.1节中说明了，两个函数相乘再积分，得到的函数的频率取决于频率较低的函数的频率。而Diffuse BRDF的频率是前三阶SH可以表示，那么环境光的频率即使再高，也没有什么过多的影响，因为得到的结果的频率最高也就三阶。

Ravi同样做了实验。他分别用前一阶、前两阶、前三阶的球谐函数来表示环境光。然后计算渲染公式。用渲染结果与实际图像进行误差计算。结果表明，使用前三阶的球谐函数来表示环境光，获得的误差为1%。

最后Ravi整理了只用前三阶SH来渲染的公式。写成了如下形式：

绿色部分代码的功能就是渲染Diffuse材质的环境光映射。

这也是历史上，只用两行代码，获得博士学位的狠人，Ravi。

并且开创了PRT的时代。

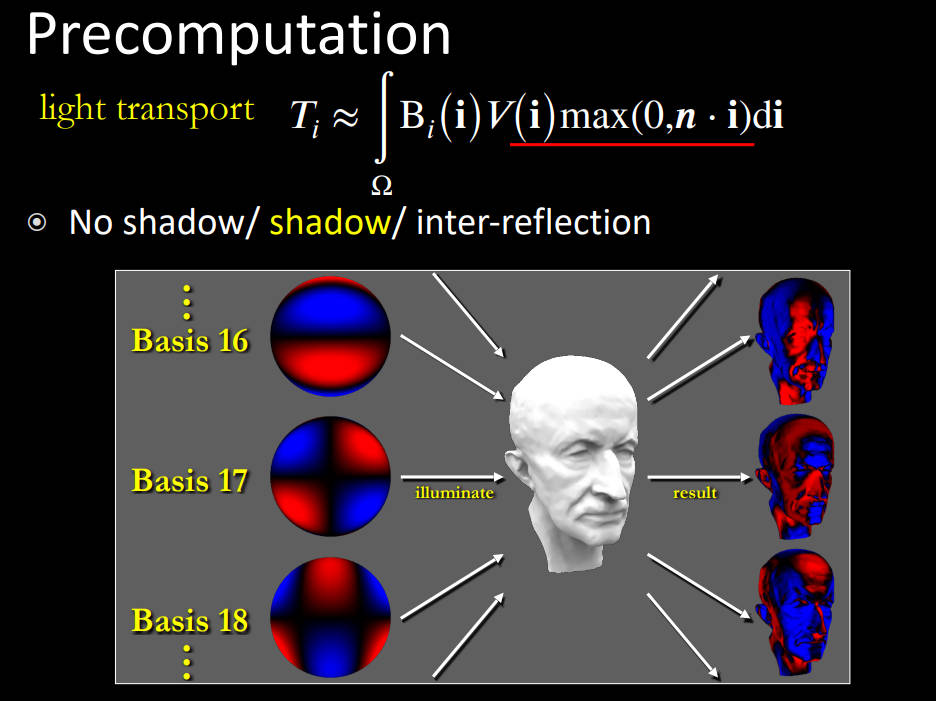
2.3.3 光辐射预计算 Precomputed Radiance Transfer（PRT）

在实时渲染中，人们更愿意将渲染函数写成相乘再积分的形式。

• lighting：球面函数
• visibility：以视点为球心的球面函数。右下角图中框出来的球为例
• BRDF：本身是4维函数但是投影到输出方向时，也是二维球面函数

对于以下方程的一种粗暴计算方法：直接相乘然后相加。但是这样做的计算量很大。举个例子，以lighting为例，假设正方体的每个面的分辨率是64X64，则对于一个shading point 需要计算6X64X64次乘法和加法。

于是有了载入史册的一篇论文 PRT：

PRT对渲染方程进行了另一种理解：将lighting 投影到light transport 上

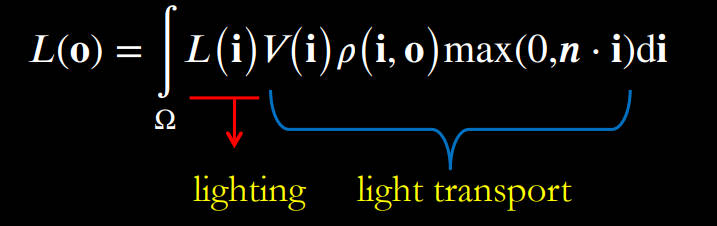
• 将lighting函数使用基函数近似
  • $L(i)\approx\sum l_i B_i(i)$
• light transport实际上是不随环境光的变化而变化的，它是物体自身性质、颜色、反射率的体现
  • 因此，light transport 完全可以预计算出来

然后对渲染方程进行计算：分两种情况讨论

2.3.3.1 Diffuse Case

Diffuse种类：diffuse 的BRDF是常数

• differentiable rendering 可微分渲染，深度学习项目？

• 实变函数：满足Fubini定理, 才可以交换顺序。$\int \sum l_i B_i(i)=\sum l_i \int B_i(i)$。在普通图像学中不考虑这个条件

• precompute就是获得了每个角度对于的值，$T_i$

• 代价：场景中的物体不能动。光源不能旋转->球谐函数的旋转性质（见2.3.1 球谐函数的性质）。

• 

• 如何理解Ti？Ti就是不同的球谐基函数在Visibility的投影

  • 

• 

2.3.3.2 Glossy Case

glossy 与 diffuse 的区别在于BRDF不再是常数

也就是说Ti不再是一个数值而是一个以观测角度为变量的函数，计算出数值的话，就是一个二维的矩阵。

2.3.3.3 Follow up works

2.3.3.4 小波

3 实时全局光照 Global Illumination （GI）

3.1 反射阴影映射 Reflective Shadow Maps

在实时渲染中，人们想要解决的全局光照是指比直接光照多一次的间接光照。也就是光线只弹射一次或者两次。如下图所示，光线最多弹射两次。

在这个场景中，Q是受到直接光照的物体，并且转为光源来照亮P。所以将Q称为次级光源。

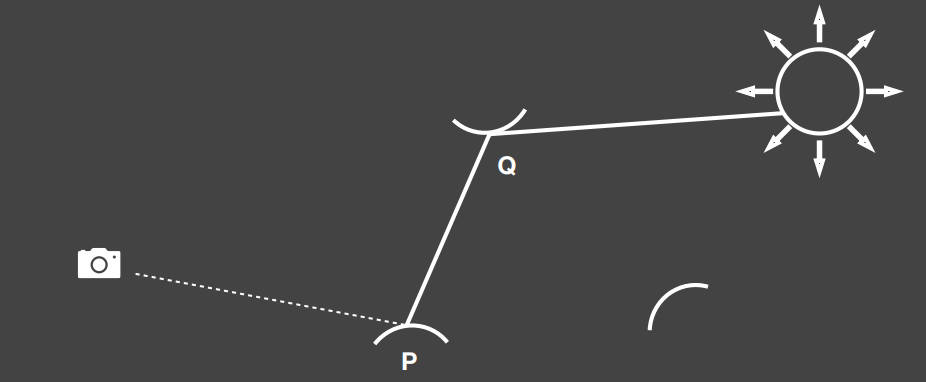
要获得P点的着色Shading，需要知道两件事：

• 哪些物体的哪些表面是次级光源？
  • 也就是说哪些区域是被光源直接照射的？->通过Shadow mapping可以获得这个信息
  • 但是使用Shadow map来表示次级光源的话，就会有shadow map分辨率大小个片光源，这个计算量是比较夸张的
• 所有次级光源区域对于P点着色的贡献是多少？->相当于以P点作为相机观测次级光源区域。但是次级光源本身也是物体，次级光源上的一个点的BRDF值在不同方向是不一样的，这是与理想点光源不一样的。而对于次级光源上的每个点都要考虑不同方向的BRDF值，这个计算量显然是非常大的。
  • 于是假设次级光源上每个点都是Diffuse的，也就是BRDF是常数

3.2 光传播体积 Light Propagation Volumes (LPV)

3.3 体素全局照明 Voxel Global Illumination（VXGL)

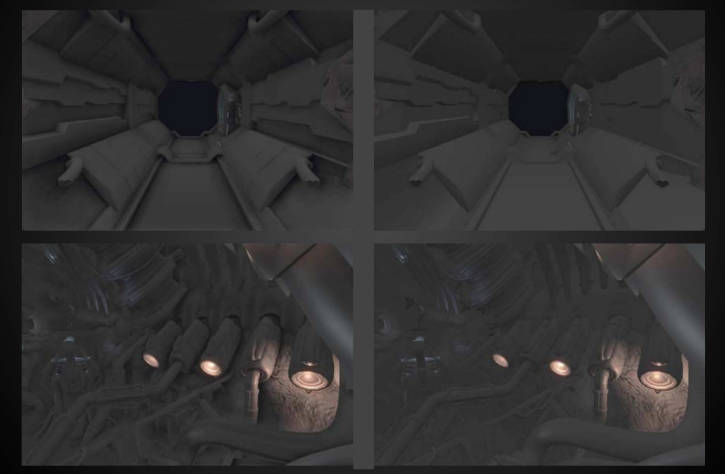
3.4 屏幕空间的环境光遮蔽 Screen Space Ambient Occlusion (SSAO)

什么是SSAO？

• 对全局光照的近似
• 在屏幕空间进行操作

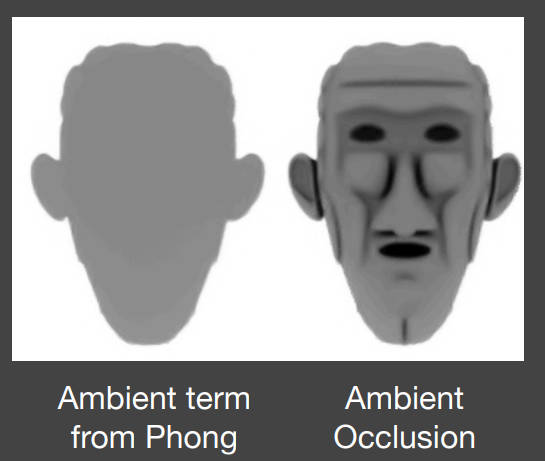
SSAO的作用：

• 增加物体的立体感。也就是物体边界的阴影感
  • 

SSAO的核心思想：

• 我们不知道入射间接光照

• 假设入射间接光照是一个常数，对于所有着色点以及所有方向

  • 这类似于布林冯氏反射模型的环境光反射的定义

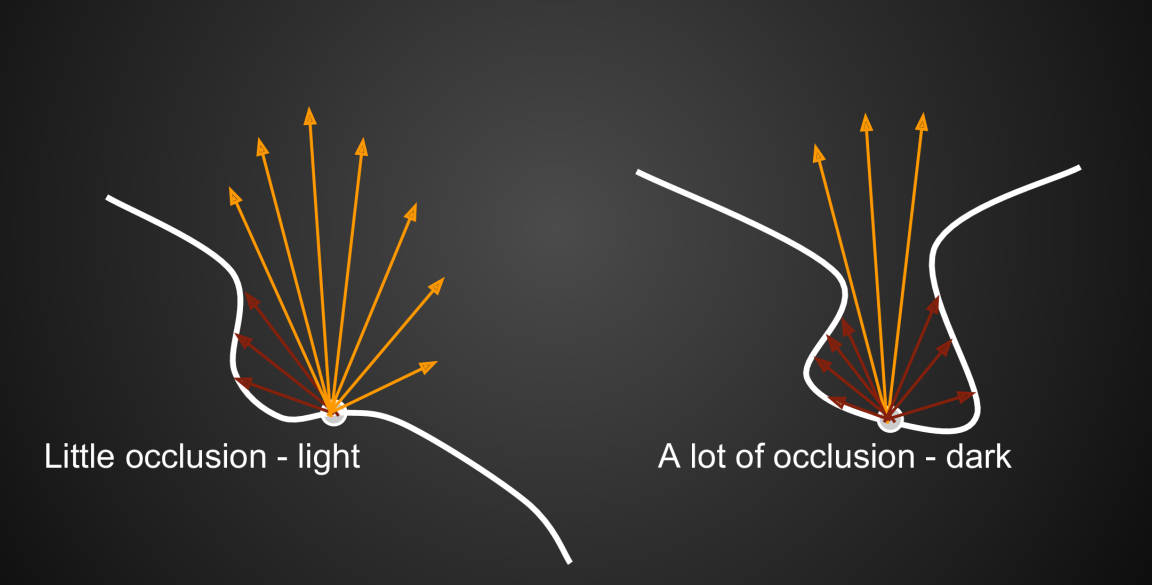
• 虽然间接光照是常数，但是所有点不是所有方向都能接收到光照 -> visibility

  • 
  • 

• SSAO计算环境光遮蔽AO时，假设物体是Diffuse的

计算思路：

仍然从渲染方程进行推导

通过实时渲染近似方程，将visibility拆出去：

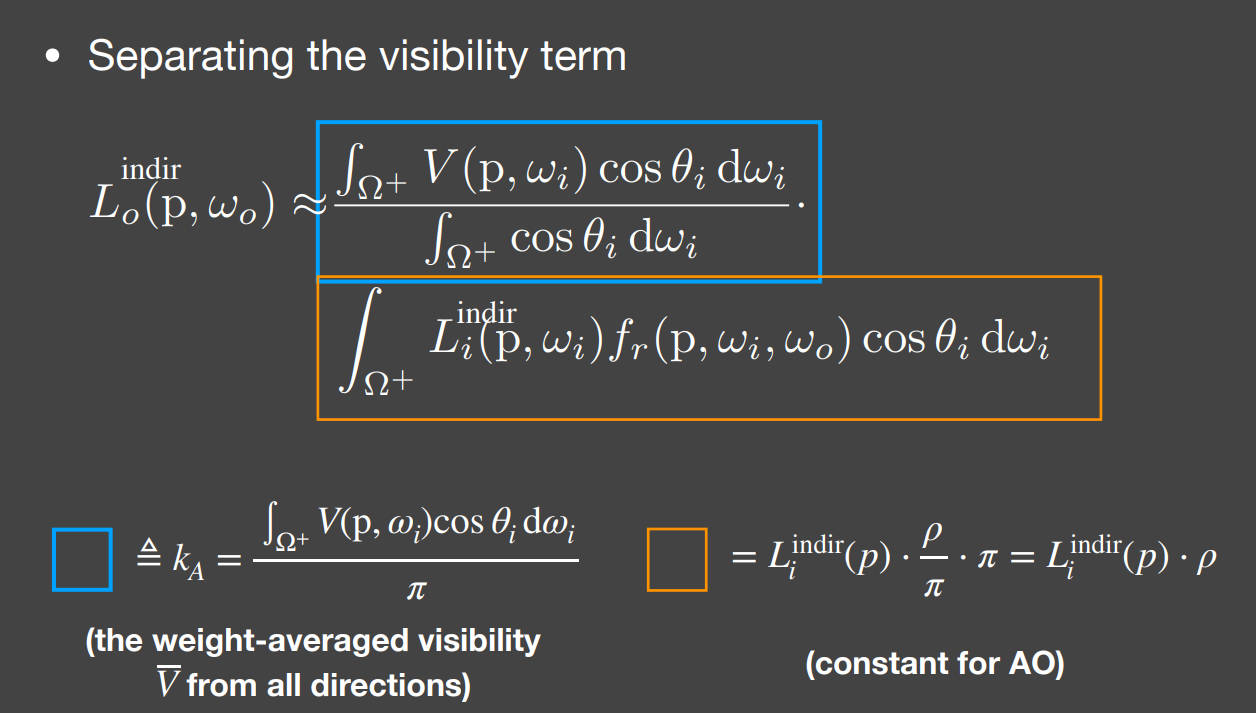
为什么可以这样拆分？

因为之前的SSAO假设中，入射间接光线$L_i^{indir}$是常数，BRDF也是常数。所以黄色框部分是一个常数。而蓝色框是visibility的加权平均。

以这个SSAO为例子进一步理解实时渲染近似方程：

• 拆分除去的部分可以理解为在$g(x)$的覆盖范围内对$f(x)$求平均

  • 

• 以往根据近似方程进行拆分时，是只对$\mathrm{d}\omega_i$进行积分，为什么在SSAO中是对$\cos \theta_i \mathrm{d}\omega_i$进行积分？

  • 

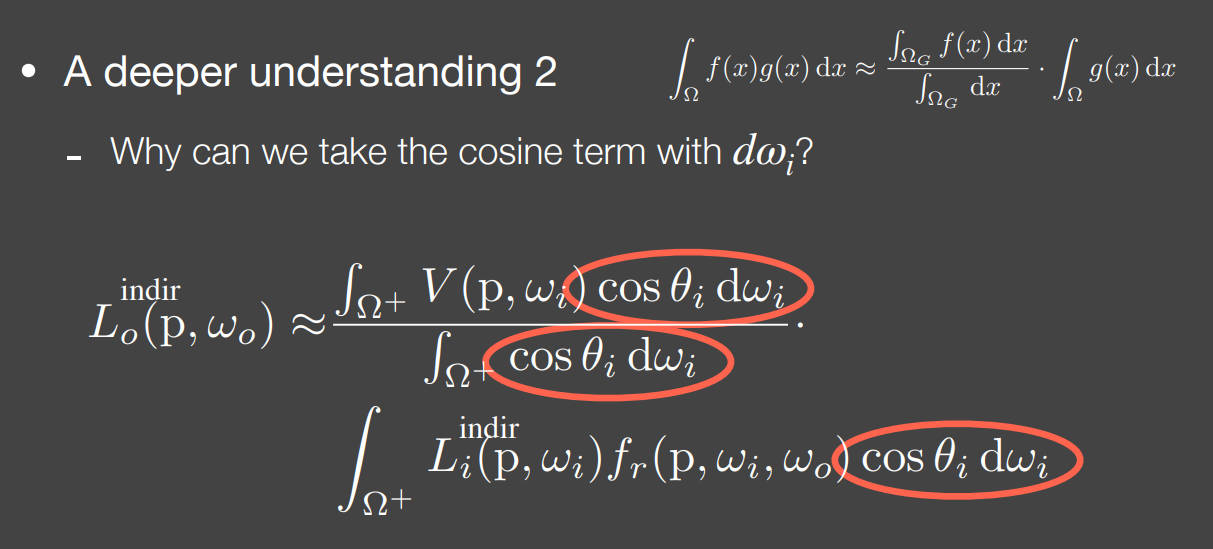
  • 解释为什么可以这样拆：引入立体角的投影

    • $\mathrm{d}\omega_i=\mathrm{d}A_i/r^2$，在单位球中r=1，那么$\cos \theta_i \mathrm{d}\omega_i$表示的是球的单位表面积投影到赤道截面的单位圆的单位面积。那么对$\cos \theta_i d\omega_i$进行半球积分，也就是对单位圆积分，也就是单位圆的面积，即$\pi$
    • 

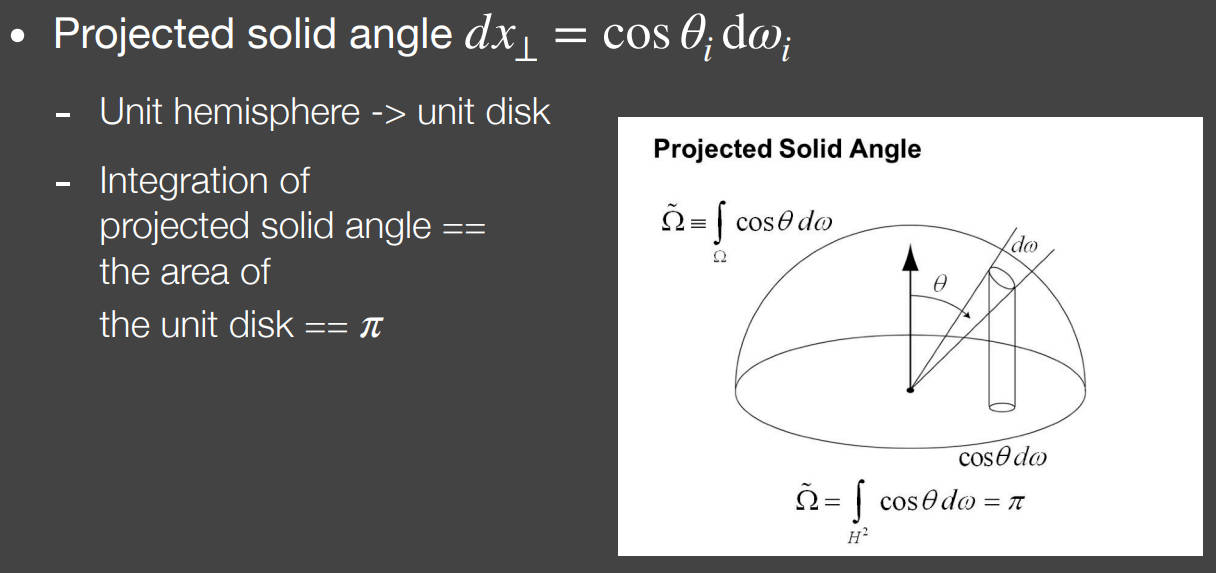
综上所述，SSAO的实时渲染近似方程可以写为：

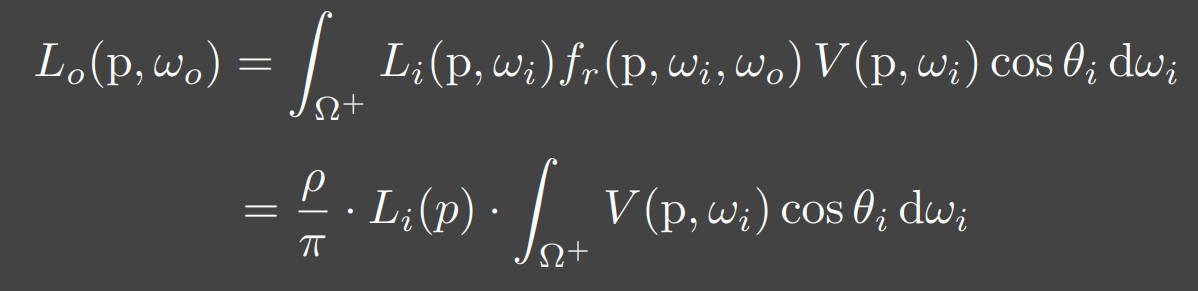
现在计算这个方程只需要知道visibility就可以了。在世界空间里，可以直接做ray tracing来获得visibility，但是在屏幕空间怎么知道visibility呢？

环境光遮蔽AO近似假设：辐射距离受限 -> 将局部遮蔽限制在一个半径为R的半球内。

如果不限制半径，那么所有光线在传播无限远的距离后可能都会遮挡，这显然是有问题的。

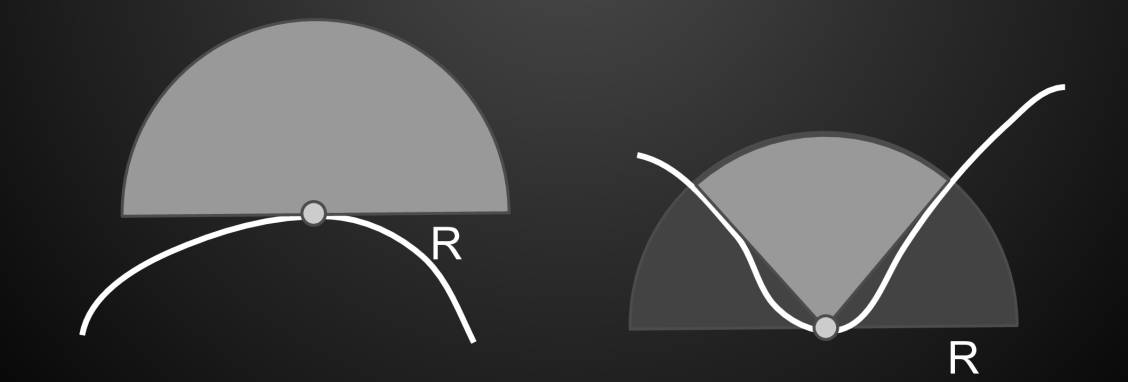
SSAO基于AO假设计算visibility的方法：

• 以着色点为球心做半径为R的单位球，在球内随机采样点，计算着色点与采样点的可见性
• 怎么计算可见性？根据z-buffer来判断，也就是采样点是大于最浅深度还是小于最浅深度的。也就是说，采样点在成像表面内部还是外部。
• 为什么是整球而不是半球？因为当时SSAO提出时，还没有存储着色点法线信息的手段。现在可以基于法线进行半球采样

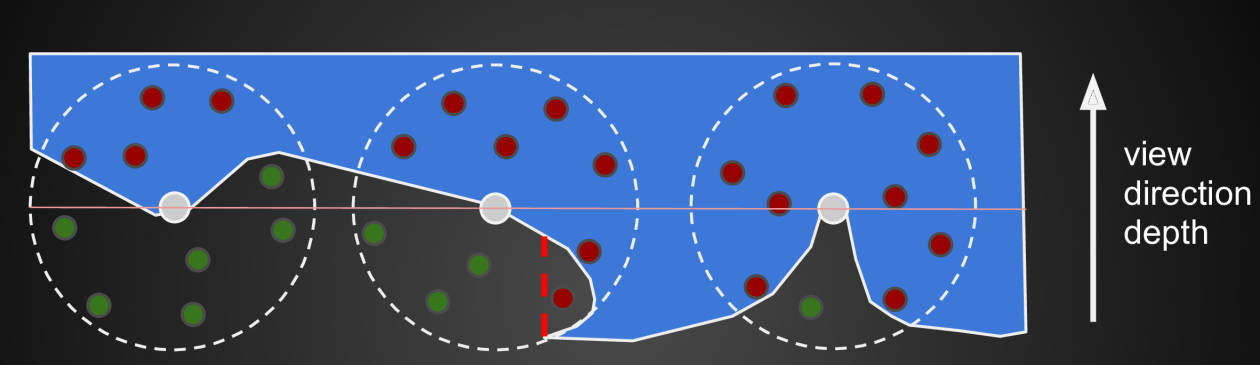
3.5 屏幕空间方向遮挡 Screen Space Directional Occlusion（SSDO）

什么是SSDO？

• SSAO的改进版本
• 不同于SSAO的环境光是常数这个假设，SSDO考虑了更精准的间接光照

SSDO的核心思想：

• 间接光照的来源->间接光源是知道的

SSAO与SSDO的区别：假设的不同

• AO：从着色点向外打出光线，如果光线没有被遮挡，说明该方向有间接光照打入着色点，否则没有。
• DO：从着色点向外打出光线，如果光线没有被遮挡，说明该方向上没有次级光源，所以没有光线、间接光源来自被遮挡方向。
• 

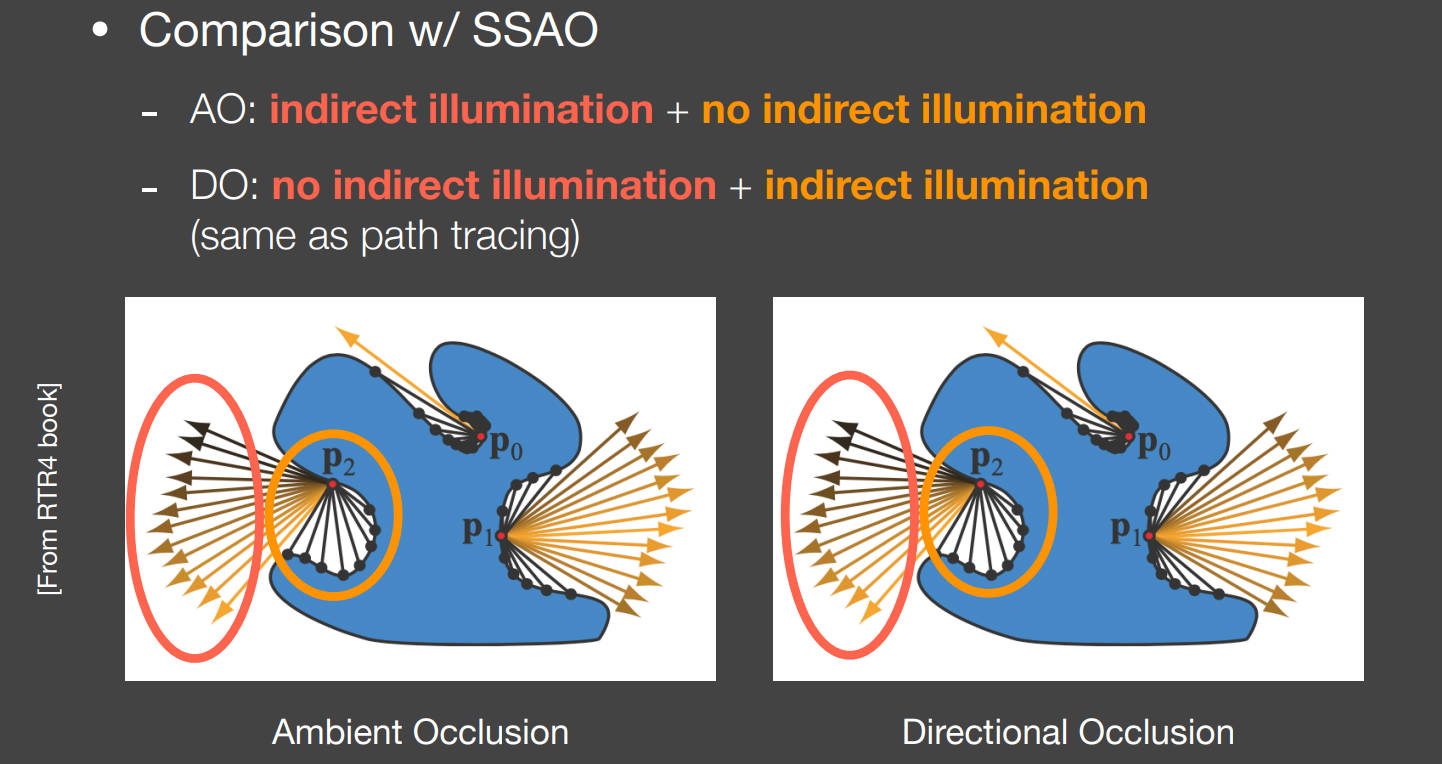
如何理解SSDO和SSAO为什么完全相反：AO表示的是来自远处的间接光照，DO表示的是来自近处的间接光照

计算方法与SSAO类似。

SSDO存在的问题：

• 表示的间接光照是小范围的

• 是通过相机的屏幕空间计算visibility的，也就是说根据深度来计算visibility是不准的，比如下图

  • 

• 屏幕空间的问题：将三维场景变成了从相机角度看过去的一个壳。那么壳背后的东西都不知道，也就是说背面的物体对着色给不出贡献

3.6 屏幕空间反射 Screen Space Reflection（SSR）

什么是SSR？

• 在屏幕空间中做光线追踪ray tracing
• 但是不要求三维的网格表面信息，而是将三维场景变成了从相机角度看过去的一个壳

SSR的两个基本任务：

• 计算任意光线与屏幕空间的“壳”的相交状态
• 计算交点对于着色点的贡献

SSR的基本思想：

• 反射光通常是屏幕空间中已经存在的物体做出的贡献（假设）

怎么计算光线与“壳”的相交情况呢？

• 对于每根光线，追踪光线的反射
• 设置一个步长，在每个步长处检测光线该点的深度值
• 如果深度值与“壳”的深度值相近，说明相交
• 显然相交的精度和计算量取决于步长的选择 -> 一个显然的想法就是让步长自适应调整

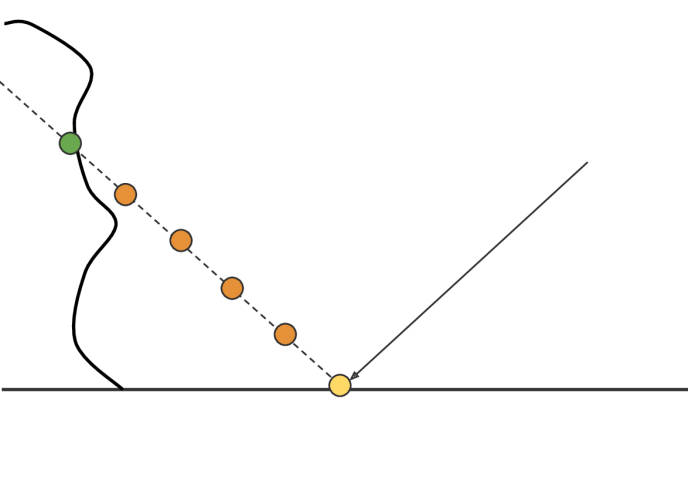
怎么自适应调整步长？

这是不是和包围盒、BVH的情况相似？将灰色矩形看作包围盒，那么光线没有与包围盒相交，自然不会与“壳”相交了

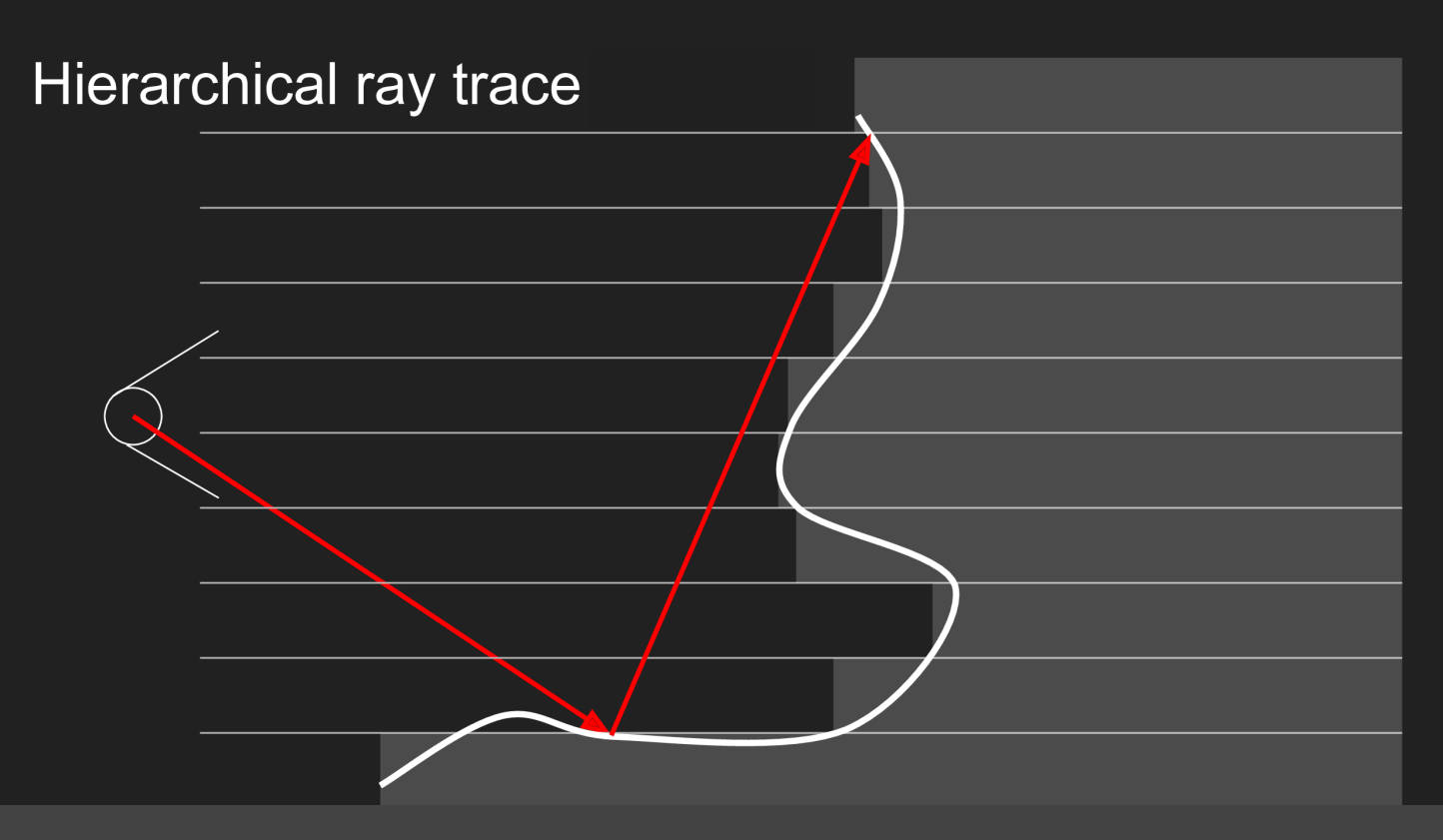
怎么计算“包围盒”？使用深度图做MipMap（Min Pooling）。

为什么是最小值池化？深度的最小值，就是这片区域中深度最浅的位置，也就是“包围盒”的边界。光线没有到边界，自然不会与“壳”相交。

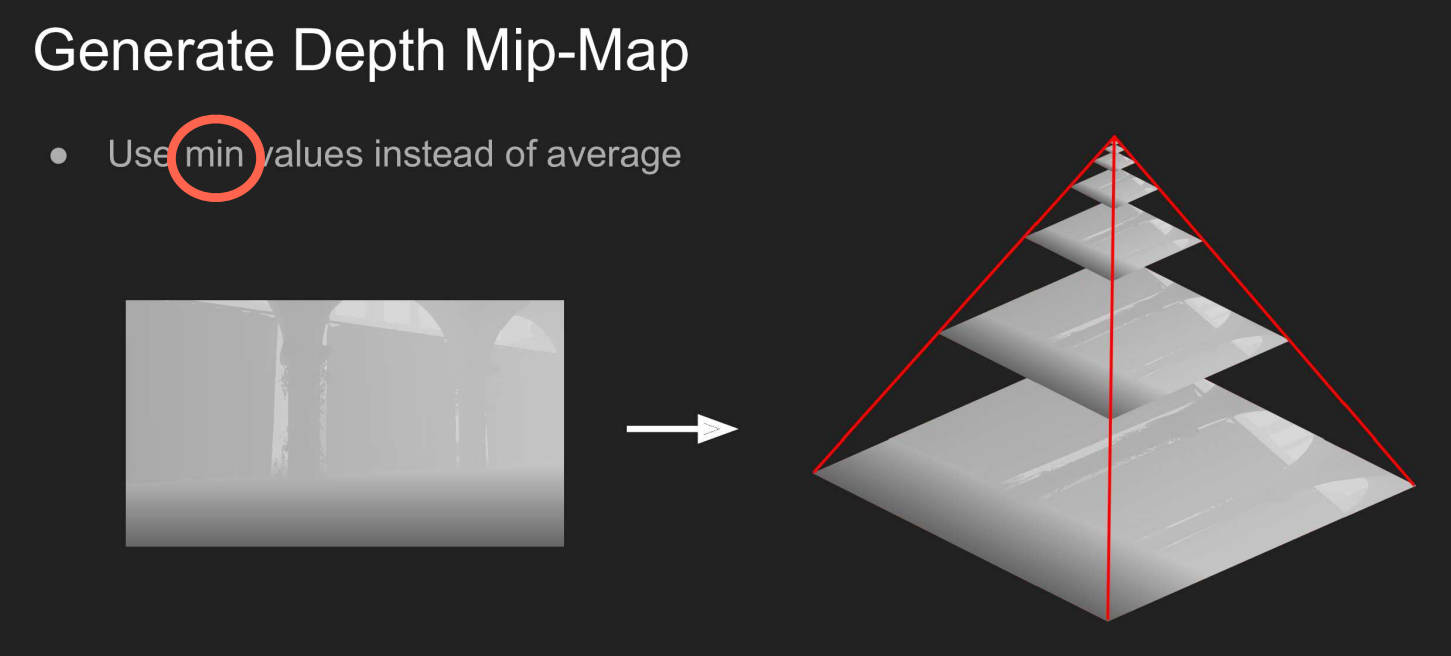
实际计算时的策略是：

• 类似二分查找
• 在最顶层，也就是pooling尺度最大的深度图进行交点查找
• 然后在交点处的像素的下一层进行查找
• 知道查找到初始深度图的位置

以上只是完成了第一步，也就是光线与壳的相交状态

第二步计算着色与path tracing一致：

应用知识

• 实时渲染（RTR）不相信复杂度，只看绝对的渲染时间