GAMES101homework记录
GAMES101homework记录
Ljy0109/Graphics_algorithms (github.com)
语法
inline
inline 是 C++ 中的关键字,用于提示编译器对函数进行内联展开。内联展开是指在调用函数的地方直接将函数的代码插入,而不是通过函数调用的方式进行执行。这样可以减少函数调用的开销,并提高程序的执行效率。
使用 inline 关键字声明的函数会被编译器视为候选进行内联展开的函数,但并不保证一定会被内联展开。编译器会根据一些策略来决定是否将函数内联展开,例如函数的大小、调用频率等因素。
示例:
1 | |
在这个示例中,add 函数被声明为 inline,因此编译器可能会将 add 函数的代码直接插入到 main 函数中,而不是通过函数调用的方式执行。
需要注意的是,inline 关键字只是对编译器的建议,编译器并不一定会采纳。通常情况下,较小的、频繁调用的函数更容易被编译器选择进行内联展开。
throw
1 | |
在满足条件后抛出错误。
std::runtime_error表示程序运行时的错误
std::transform()
示例:
1 | |
std::transform 是 C++ 标准库中的一个算法,它用于对一个容器(或者两个容器)中的元素应用指定的操作,并将结果存储到另一个容器中。该算法定义在 <algorithm> 头文件中。
std::transform 函数的常用形式有以下几种:
- 单容器变换:
1 | |
该函数接受一个输入迭代器范围 [first1, last1) 表示输入容器的范围,一个输出迭代器 result 表示输出容器的起始位置,以及一个一元操作函数 op,用于对输入容器的元素进行变换,并将结果存储到输出容器中。
- 双容器变换:
1 | |
该函数接受两个输入迭代器范围 [first1, last1) 和 [first2, ... 来源于第二个容器的元素进行操作,并将结果存储到输出容器中。
在示例提供的代码中,使用的是第一种形式的 std::transform 函数,它对一个输入容器中的每个元素应用指定的操作,并将结果存储到输出容器中。
map
示例:
1 | |
std::map 是 C++ 标准库中的一个关联容器,它提供了键-值对的映射关系,并且能够根据键的排序规则自动对键进行排序。std::map 的定义位于 <map> 头文件中。
std::map 的特点包括:
- 键值对:
std::map中的每个元素都是一个键值对,其中键和值可以是任意类型的数据,键和值之间存在映射关系。 - 排序:
std::map会根据键的排序规则自动对键进行排序,默认情况下是按照键的自然顺序进行排序,但也可以通过提供自定义的比较函数来定义排序规则。 - 唯一性:
std::map中的键是唯一的,每个键只能对应一个值,如果尝试插入一个已经存在的键,则插入操作会失败。 - 搜索:
std::map提供了高效的搜索操作,可以根据键来快速查找对应的值。
使用 std::map 的一般步骤包括:
- 包含头文件:
#include <map> - 定义
std::map对象:std::map<KeyType, ValueType> myMap; - 插入元素:
myMap[key] = value;或者myMap.emplace(key, value); - 访问元素:
myMap[key]或者myMap.at(key) - 遍历元素:使用迭代器进行遍历,或者范围遍历(C++11 及以上版本)。
例如:
1 | |
这段代码创建了一个 std::map 对象 myMap,并向其中插入了两个键值对。然后使用下标运算符和 .at() 方法访问元素,并使用范围遍历方式遍历所有元素。
.emplace() 是 C++ STL 容器中的一个成员函数,用于在容器中直接构造一个新的元素。它的参数会被传递给容器中元素的构造函数,从而在容器中直接构造一个新的元素。.emplace() 函数通常用于避免不必要的拷贝或移动操作,因为它可以在容器中直接构造新的元素,而不需要先创建一个临时对象。
fabs()
fabs(dx) 是 C++ 标准库 <cmath> 中的函数,用于计算一个浮点数 dx 的绝对值。
在 C++ 中,fabs() 函数的功能是返回一个浮点数的绝对值。如果参数是整数类型,则会隐式转换为浮点数再计算绝对值。
static
static function()
static修饰的静态函数被限定在本源码文件中,不能被本源码文件以外的代码文件调用。而普通的函数,默认是extern的,也就是说,可以被其它代码文件调用该函数。
静态函数只是在声明他的文件当中可见,不能被其他文件所用。因此定义静态函数有以下好处:
- 其他文件中可以定义相同名字的函数,不会发生冲突。
- 静态函数不能被其他文件所用。
- 静态函数会被自动分配在一个一直使用的存储区,直到退出应用程序实例,避免了调用函数时压栈出栈,速度快很多。
- static函数在内存中只有一份,普通函数在每个被调用中维持一份拷贝。
static 成员变量和成员函数
- private static 和 public static 都是静态变量,在类加载时就定义,不需要创建对象
- private static 是私有的,不能在外部访问,只能通过静态方法调用,这样可以防止对变量的修改
- static 成员函数只能访问static成员变量,非static成员函数可以访问static成员变量
static函数和私有函数的区别
static函数避免了调用函数的进栈出栈,速度比私有函数快。这在光栅化、渲染等实时任务里是一个有效加速的方法- 为什么不将私有函数变为静态函数?因为静态函数不能直接访问成员变量
- 为什么不使用静态私有函数?因为静态私有函数只能访问静态成员变量
使用位运算同时表示两个种类
示例:
1 | |
使用operator关键词重构位运算符,以下是使用示例:
1 | |
v[0].w()
在C++中,v[0].w()通常表示对一个自定义类型或结构体中的第四个成员进行访问。
也就是说从0到3的元素默认表达为:v[0].x() v[0].y() v[0].z() v[0].w()
算法
Bresenham 直线光栅化算法
Bresenham布雷森曼算法 - Blog of Mr.Juan (ljy0109.github.io)
透视矫正系数
如何获得屏幕中二维点对应的深度信息?
通过二维点对应到三维空间所在的三角平面的三个顶点进行插值。
如何进行插值?
通过三角形的重心坐标:
为什么不在二维平面进行插值?
首先,肯定不能使用二维点进行重心插值。因为二维点没有深度。
那么同一个点在二维平面的重心坐标和在三维空间中的重心坐标一样吗?
答案是不一样。重心坐标是三角形内部划分的三个三角形的面积。平面的三角形是三维空间三角形的投影,难道从不同视角看过去,三个三角形的面积比例都是不变的吗?当然不是
所以必须计算目标点在三维空间的重心坐标。
怎么计算呢?
思考一下从三维空间到平面坐标,顶点的变化:
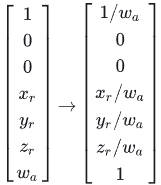
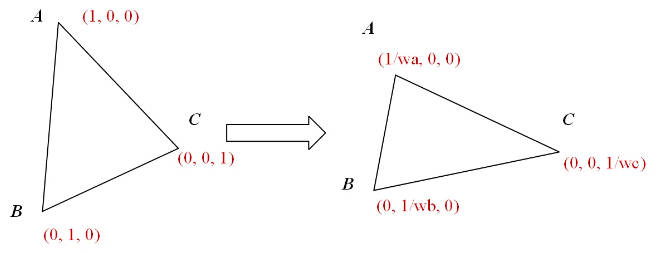
假设在屏幕空间中求得得重心坐标$ (a,b,c)(1/w_a,0,0),(0,1/w_b,0),(0,0,1/w_c)$插值即可(这里把它当作普通数据插值,之后再保证和为1),插值后的形式即是校正后的重心坐标:
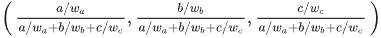
那么插值公式就是:
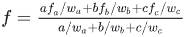
此时插值的不一定是坐标值,也可以是颜色值,纹理值等等
法向量变换矩阵
使用矩阵对点进行空间变换是图形学中的常见操作,假设变换矩阵为,我们需要变换切向量(由点定义) 以及与其垂直的法向量。(和均为列向量)
假设点经过变换后为,点经过变换后为,为变换后的切向量:
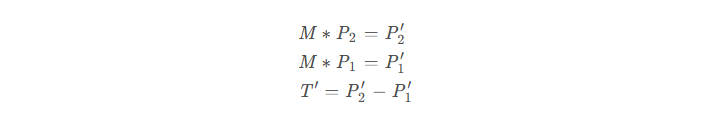
对于原切向量,我们希望找到一个矩阵,使得:
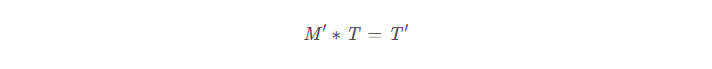
我们直接令试一下:
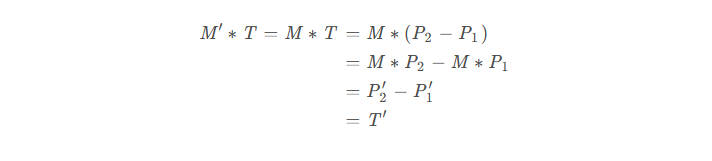
可见对于切向量,我们可以直接使用对其进行变换。
对于法向量,我们有(注意,第一个公式中的点号表示点积):
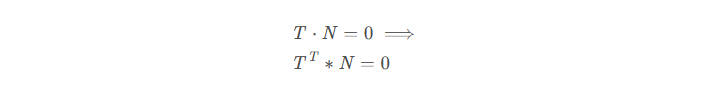
假设变换后的法向量为,我们希望仍然保持其与(的变换后向量)的垂直(注意,第一个公式中的点号表示点积):
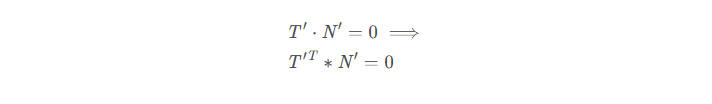
假设用于变换法向量的矩阵为G,则应有:
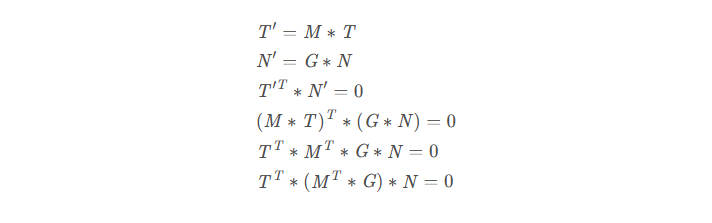
由于我们知道:
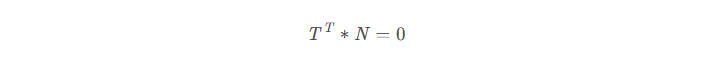
所以我们只要令(注意,这只是一种可能的取值,并不是唯一取值,我们的目的也仅是需要获得一种可能的取值):
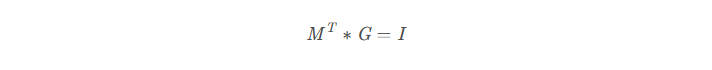
便可以满足上面的等式 :
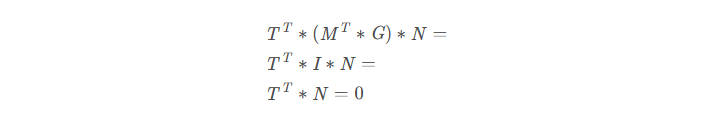
所以变换法向量,我们需要使用普通变化矩阵逆的转置(或者说转置的逆,对于可逆矩阵,其转置矩阵的逆矩阵等于其逆矩阵的转置矩阵)
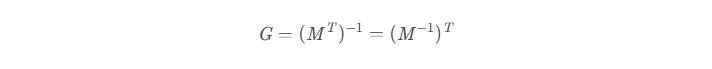
菲涅尔反射方程
当光线碰撞到一个表面的时候,菲涅尔方程会根据观察角度告诉我们被反射的光线所占的百分比。利用这个反射比率和能量守恒原则,我们可以直接得出光线被折射的部分以及光线剩余的能量。将其应用在BRDF当中,我们就可以更加精准的计算出渲染方程中的值。
我们假设入射光与法线的夹角为,折射光与法线的夹角为 。由于折射还和介质的折射率有关,例如空气中的光射入水中,我们需要知道空气和水分别对应的折射率,我们再假设入射光所在介质的折射率为 ,物体的折射率为。由于光的偏振(极化)现象,我们可以得到 S偏振光 和 P偏振光 分别对应的菲涅尔方程,如下:
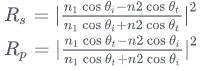
根据折射定律:

可以推导出:
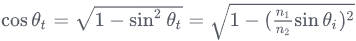
因此上面的菲涅尔方程可以写成没有的形式:
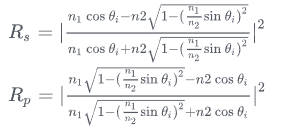
如果我们不考虑偏振的情况,那么菲涅尔方程即是上面两者的平均值:
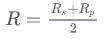
利用菲涅尔方程,我们就可以根据不同的反射率画出 R 与的对应关系图,如下:
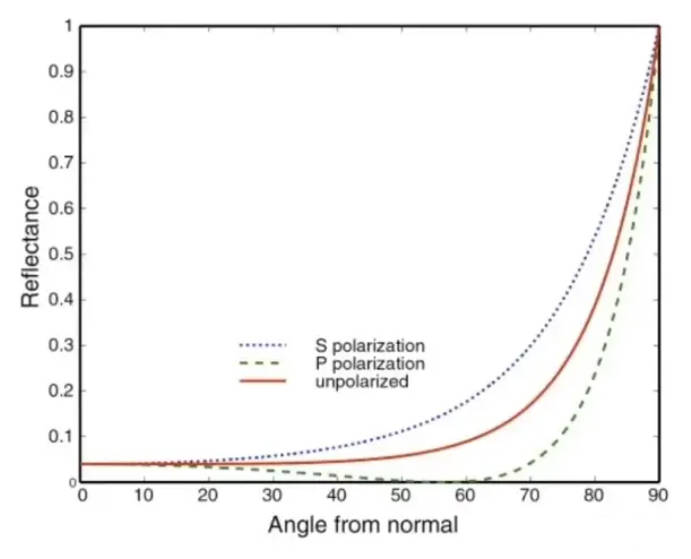
代码示例:
1 | |
折射方程的计算逻辑
折射光线的强度因子
折射光线的强度因子(transmission coefficient)是指光线在介质界面发生折射时,入射介质和折射介质之间能量的传递比率。在一般情况下,该强度因子由折射角和入射角以及介质的折射率决定。
数学公式为:
其中:
- 是强度因子;
- 是入射介质的折射率;
- 是折射介质的折射率;
- 是入射角的余弦值。
这个公式的理解是,当 大于等于 0 时,光线能够穿透介质界面进行折射;而当小于 0 时,发生全反射,光线无法穿透介质界面。
折射光线的方向向量
折射光线的向量公式可以表示为:
其中:
- 是折射光线的方向向量;
- 是入射介质的折射率与折射介质的折射率之比;
- 是入射光线的单位方向向量;
- $ \cos(\theta_{\text{in}})$是入射角的余弦值;
- 是折射光线的幅值,表示入射光线与法线夹角的正弦值;
- 是法线的单位方向向量。
代码示例
1 | |
MT算法:射线与三角形的交点
不用掌握推导,只用记住结论
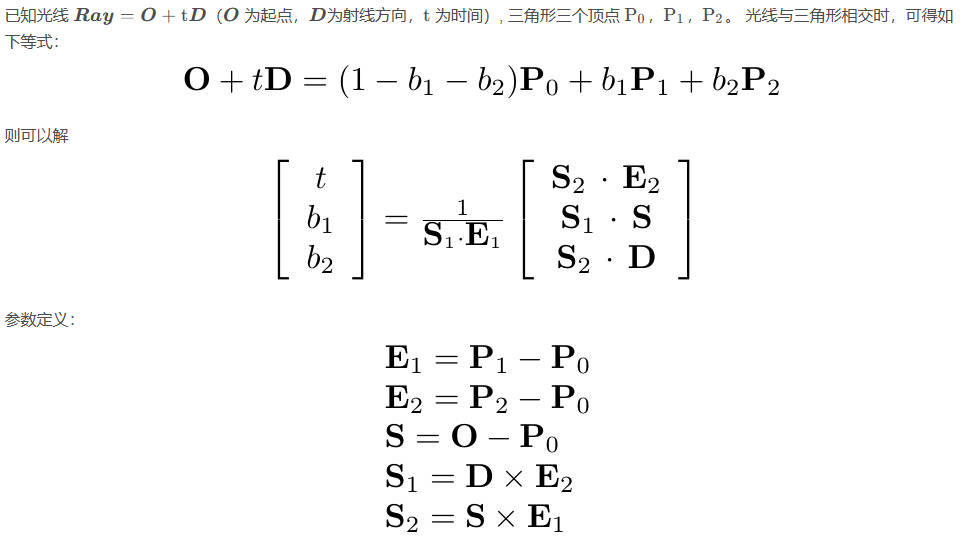
推理过程:
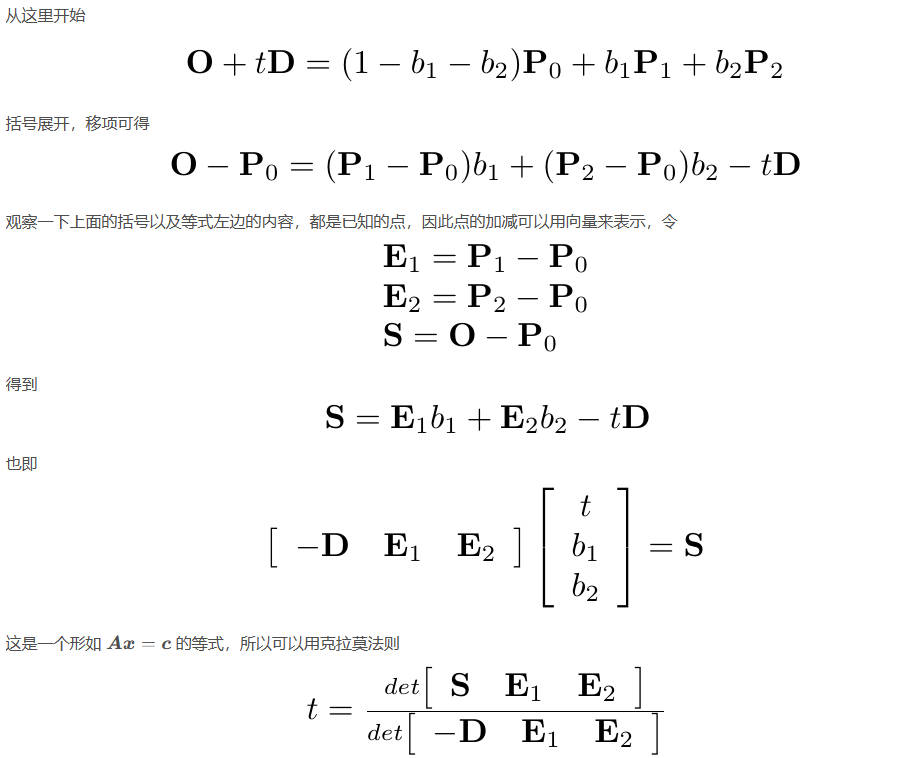
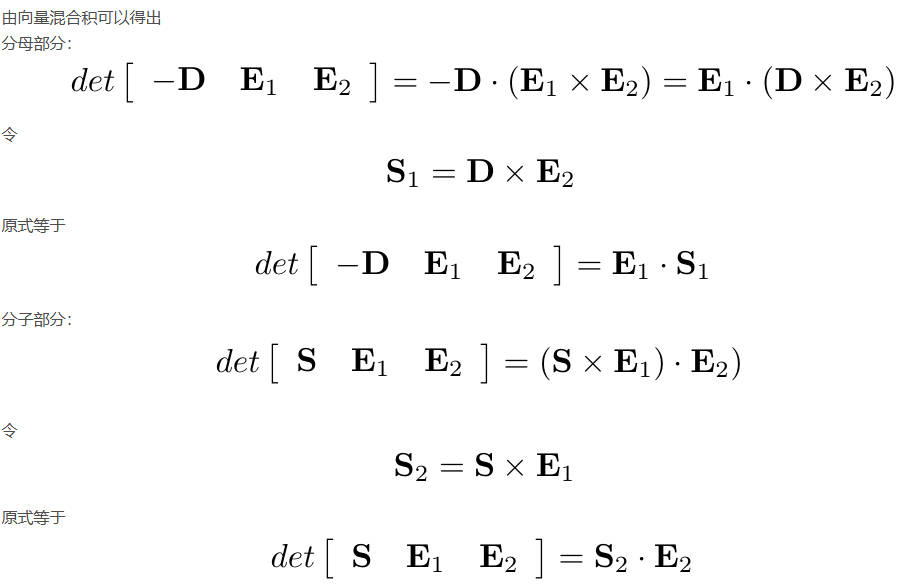
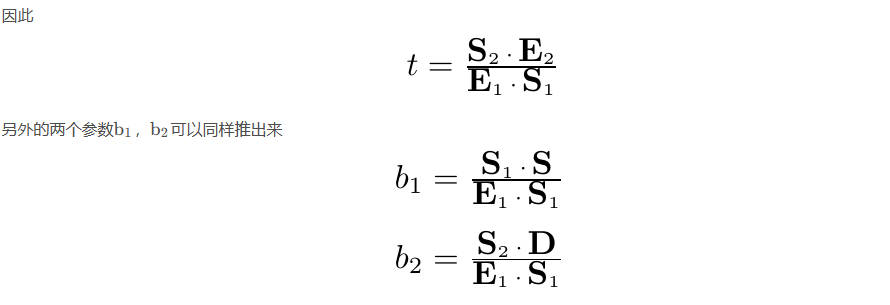
代码示例:
1 | |
由局部坐标系到世界坐标系的转换
[补充知识]由局部坐标系到世界坐标系的转换 - 知乎 (zhihu.com)
在生成采样方向时,一般生成的采样方向都是定义在点的局部坐标系(也叫切线空间)中的,很多时候都需要把采样方向由局部坐标系转换到世界坐标系下进行后续计算(如下图)。
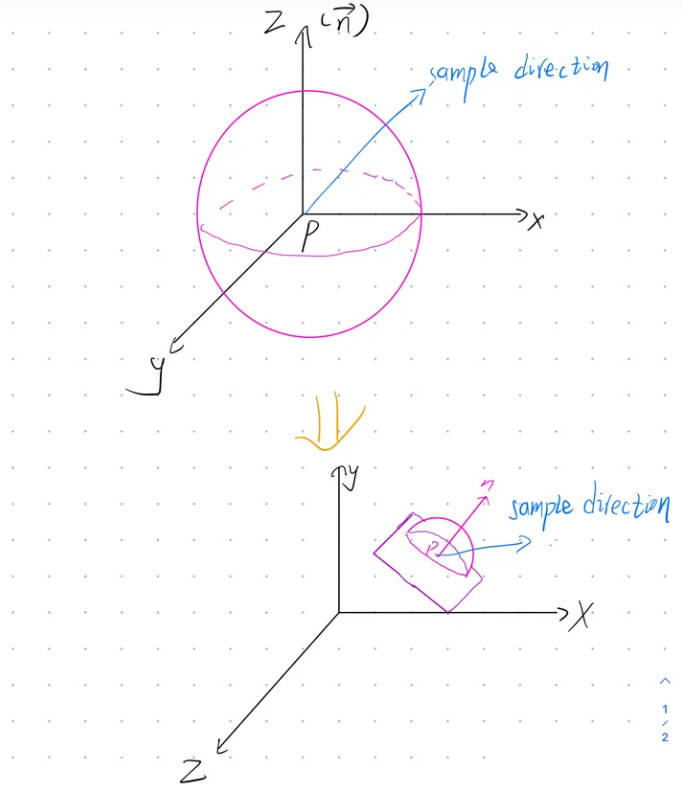
在光线追踪中,从相机光心打出射线与物体进行相交,然后需要在交点处随机采样一个反射光线。
怎么随机采样呢?那就是画一个以交点为中心的单位上半球,然后在球的表面随机选取一个点,从球心指向表面点的向量就是随机采样的光线。
代码示例:in Material.hpp
1 | |
但是这个采样光线是在以球心作为原点的局部坐标系中表示。怎么把这个光线变换到世界坐标系?
通过交点平面的法向量。法向量N是世界坐标系的表示,那么使用N来表示采样光线的话,采样光线就是世界坐标系下的了。
怎么表示呢?思考这样一件事,法向量N是通过世界坐标系的基向量来表示的。现在如果以法向量N作为局部坐标系的基向量,那么使用N来表示采样光线是不是就相当于使用世界坐标系的基向量来表示。
但是法向量N就一个向量,所以需要通过法向量N来生成另外两个基向量,使其可以表示局部坐标系下的点。
引入切线空间 tangent space
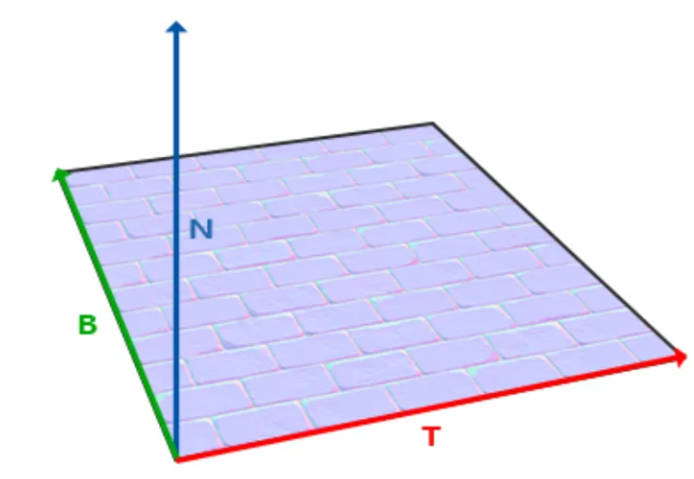
构造方法:
计算在x-z平面或者y-z平面中与N正交的单位向量,获得副切线向量B,然后获得切线向量T
NBT三个互相正交的向量构成局部坐标系。半球表面随机采样的点(x,y,z)对应NBT三个基向量,线性组合就变成世界坐标系了。变换后的采样光线仍然是单位向量。
代码示例:
1 | |
思考代码中的C为什么这么计算?为了保证C和N正交,且C是单位向量
思考变换后的a和原本的a表示的是半球上相同的点吗?没想过,不过本来就是随机点,所以没关系
GAMES101:作业7的教程
Games101:作业7(含提高部分)_intersection scene::intersect(const ray &ray) cons-CSDN博客