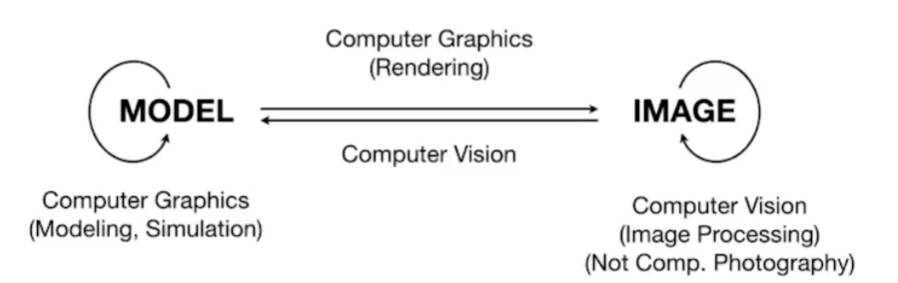
GAMES101_现代计算机图形学基础

四大部分：光栅化、几何、光线追踪、模拟动画

Bigwings - youtube

1 线性代数基础知识

向量写作 $\overrightarrow{a}$ ， $\|\overrightarrow{a}\|$ 是向量 $\overrightarrow{a}$ 的长度， $\hat{a}=\overrightarrow{a}/\|\overrightarrow{a}\|$ 是单位向量，也就是 $\overrightarrow{a}$ 的方向

在坐标系下向量可以写作$ \bold{A} = \left( \begin{matrix} x\ y \end{matrix} \right) $和$ \bold{A}^T = (x,y)$

1.1 向量乘法

1.1.1 向量点乘

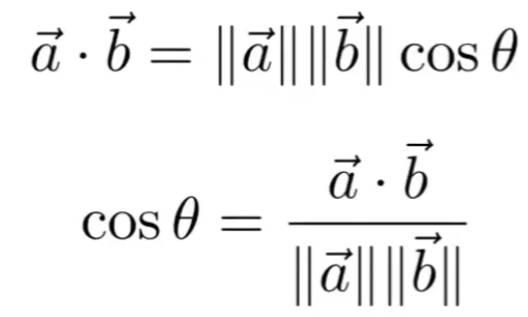
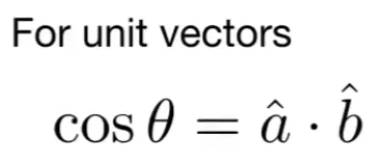
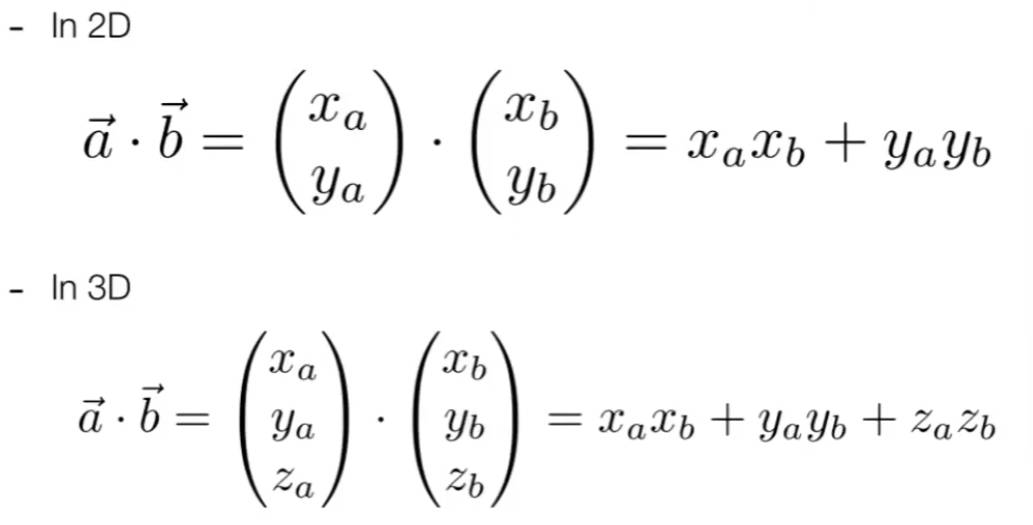
向量点乘在图形学中的主要两个作用是

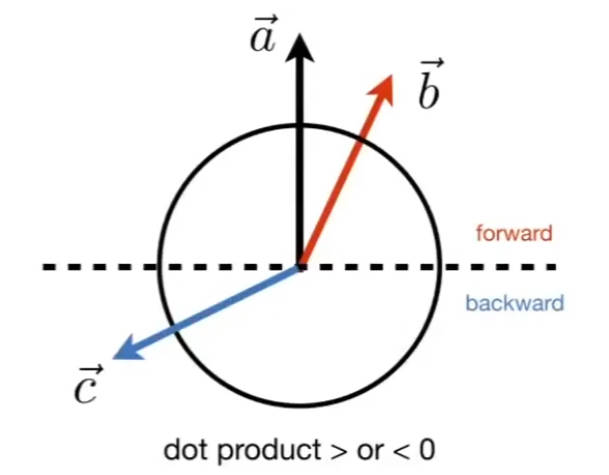
获得两个向量间的夹角。进一步说，可以通过点乘的值判断两个向量的接近程度，或是向量的方向是否一致。
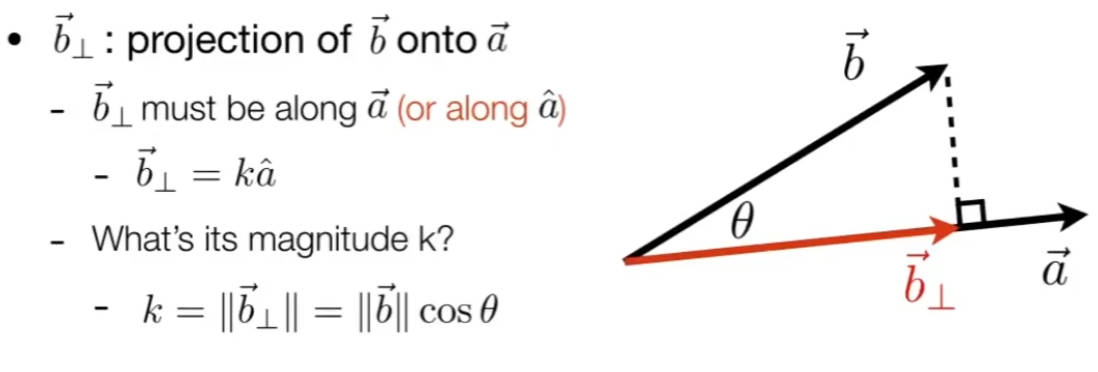
将一个向量投影到另一个向量中

点积的应用：判断物体反光

1.1.2 向量叉乘

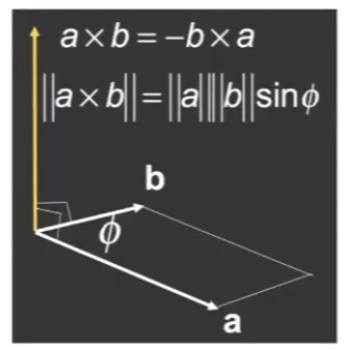
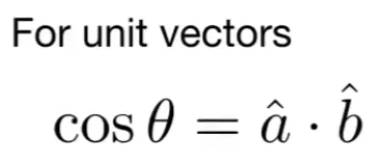
叉乘不满足乘法交换律

叉乘的作用：使用两个向量可以建立一个三位坐标系

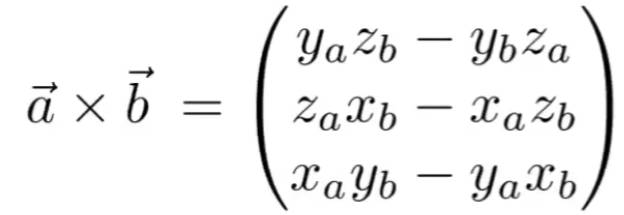
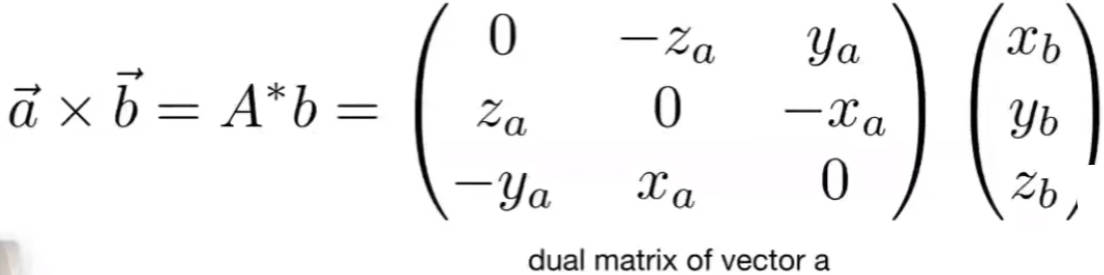
叉乘的作用：

使用两个向量可以建立一个三位坐标系
在建立好的坐标系中，可以通过叉积来判断两个向量的左右关系
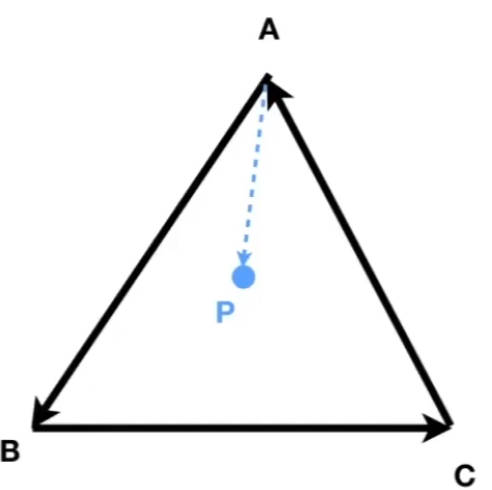
判断某向量或某点是否在一个区域的内部或外部。比如三角形，方法是将目标向量与三个边向量进行叉乘，如果在叉积的符号相同，则说明在内部。（适合任意凸多边形）

1.2 正交坐标公式

1.3 矩阵

相乘结果的矩阵中的 $(i,j)$ 元素等于第i行的A与第j列的B相乘相加

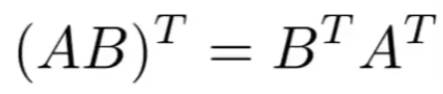
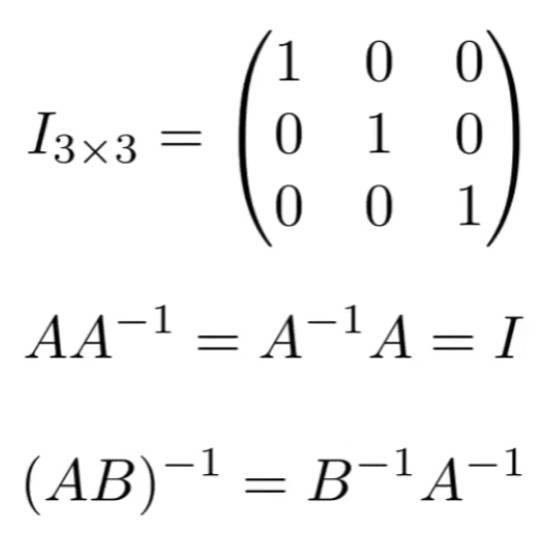
1.3.1 向量的点积和叉乘写成矩阵形式

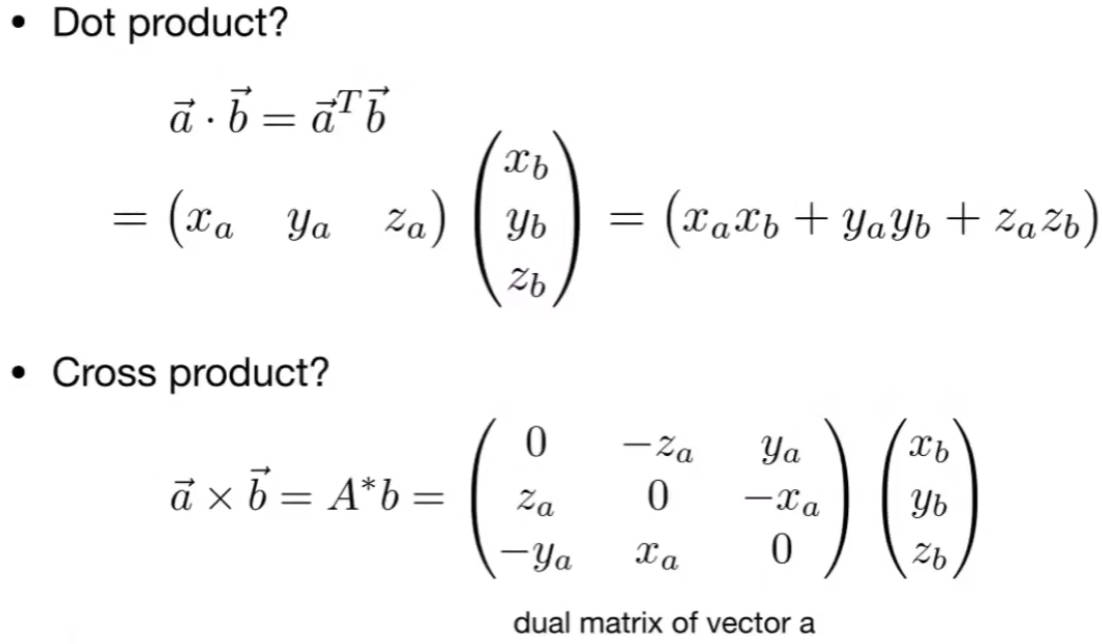
2 变换 Transformation

2.1 线性变换

2.1.1 缩放变换 Scale Transform

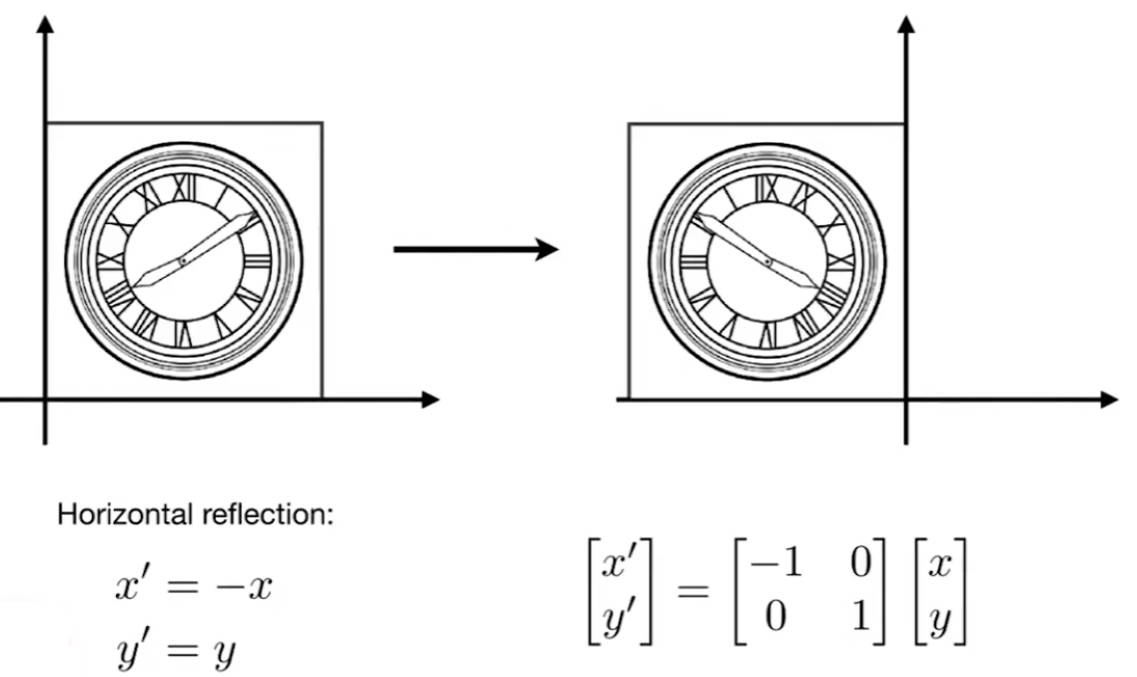
2.1.2 反射变换 Reflection transformation

2.1.3 切向变换 Shear Matrix

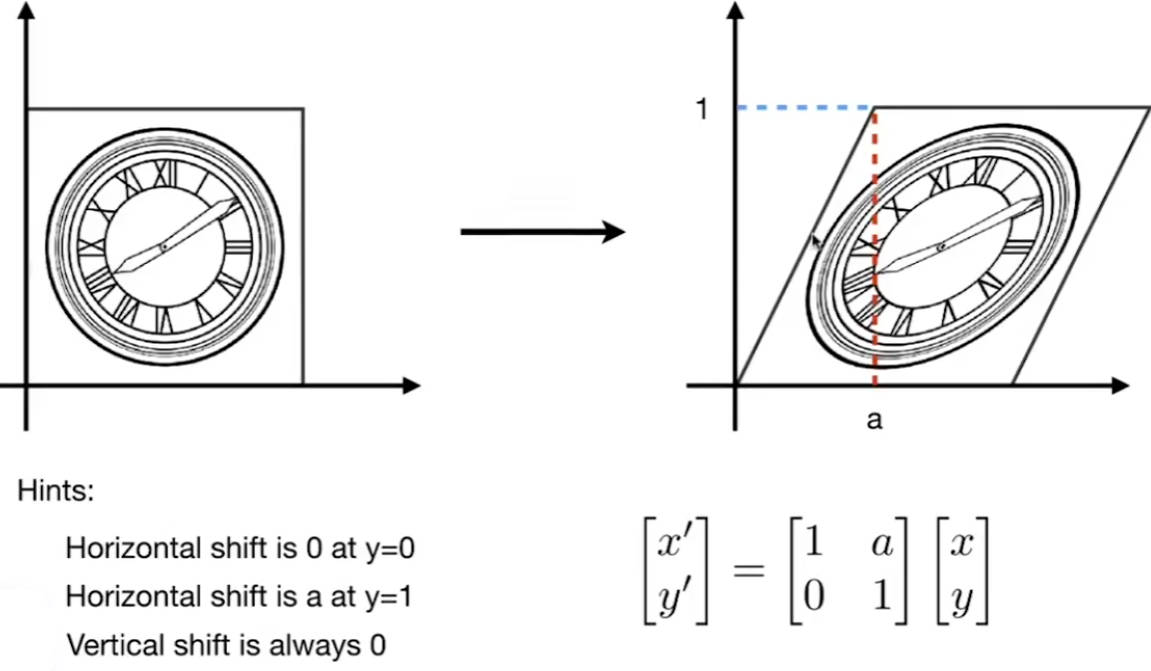
2.1.4 旋转变换 Rotation Transform

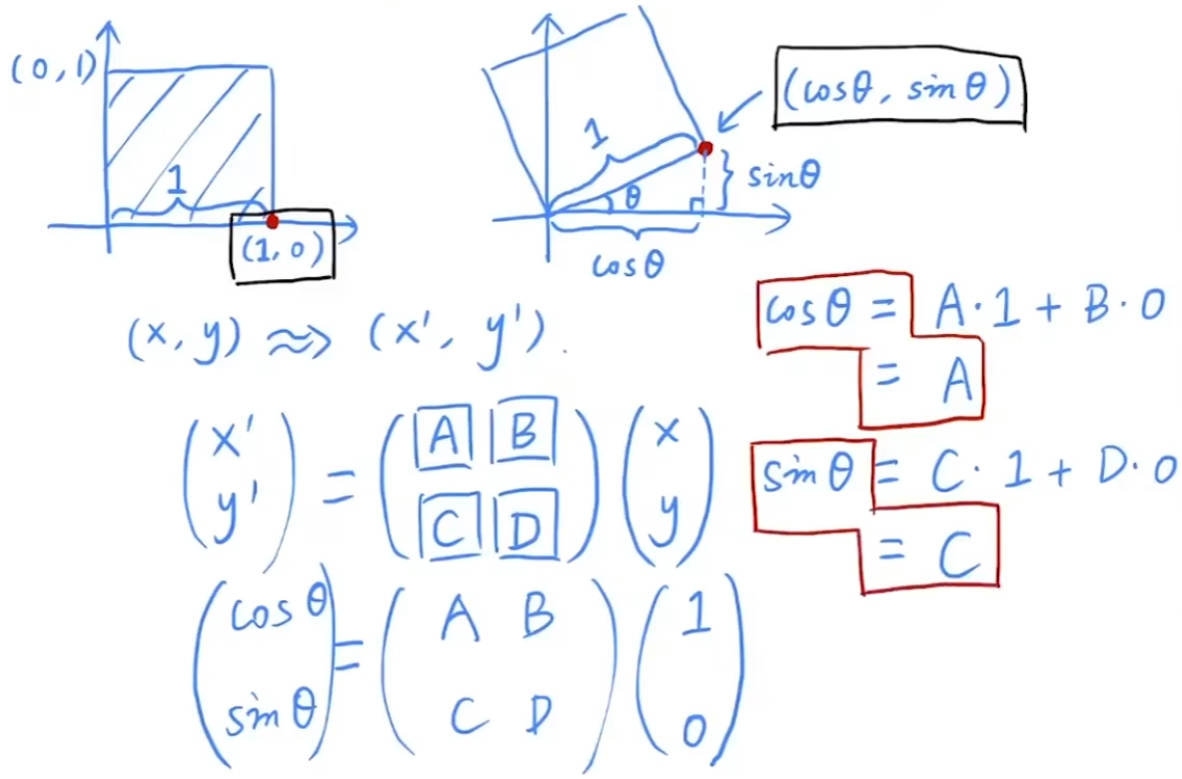
旋转矩阵的一个特殊性质：

旋转矩阵的逆=旋转矩阵的转置，也就是说旋转矩阵是正交矩阵

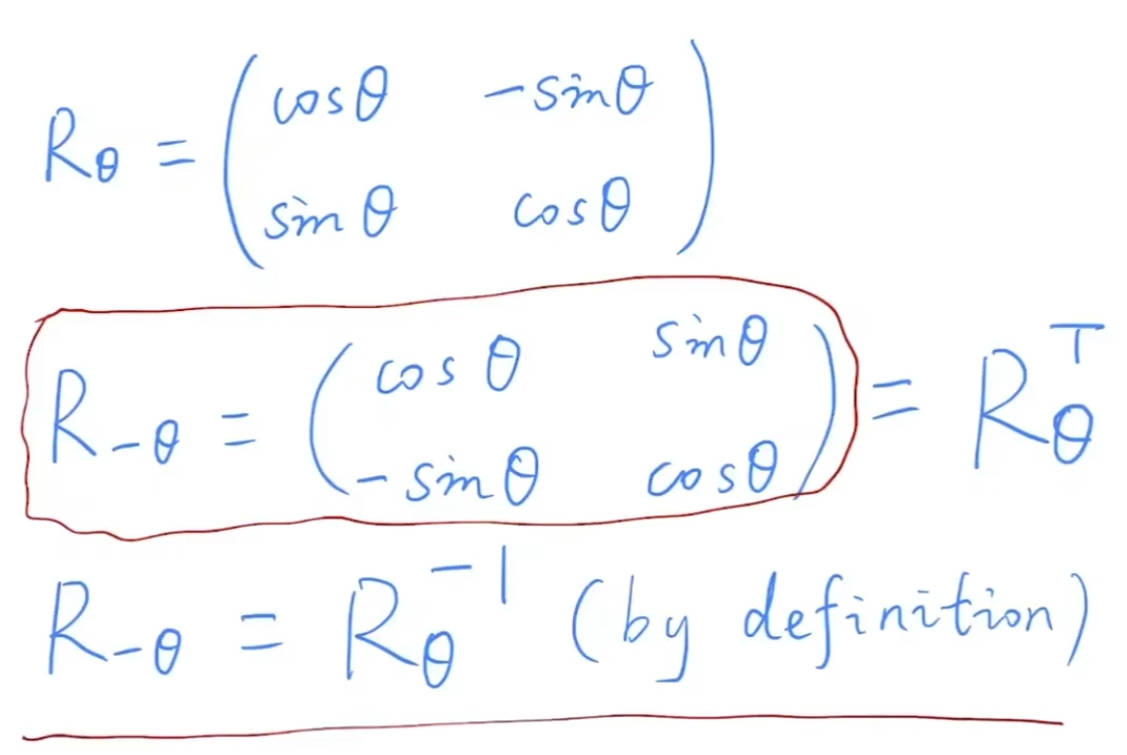
2.1.5 线性变换

上述提到的四种变换类型均可以写成以下这种形式。也将可以用这种形式表示的变换统称为线性变换

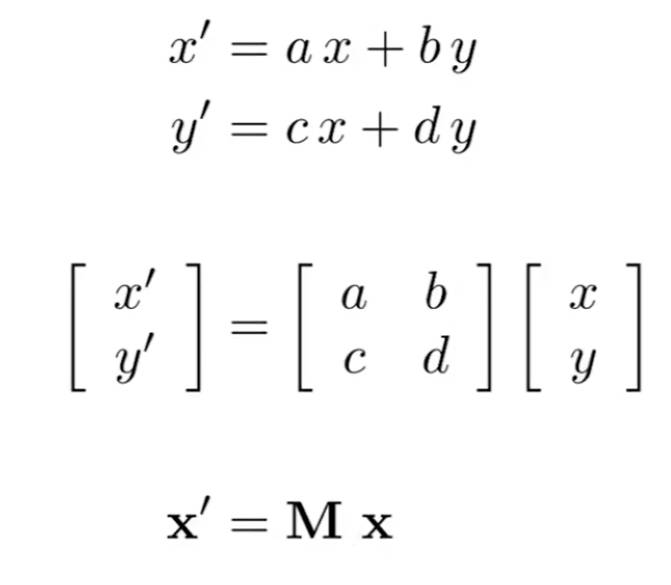
2.2 仿射变换

2.2.1 平移变换和齐次坐标

平移变换不能直接用上述矩阵的形式表达，于是引入了第三维度和齐次坐标。并将上述线性变化和平移变换统称为仿射变换

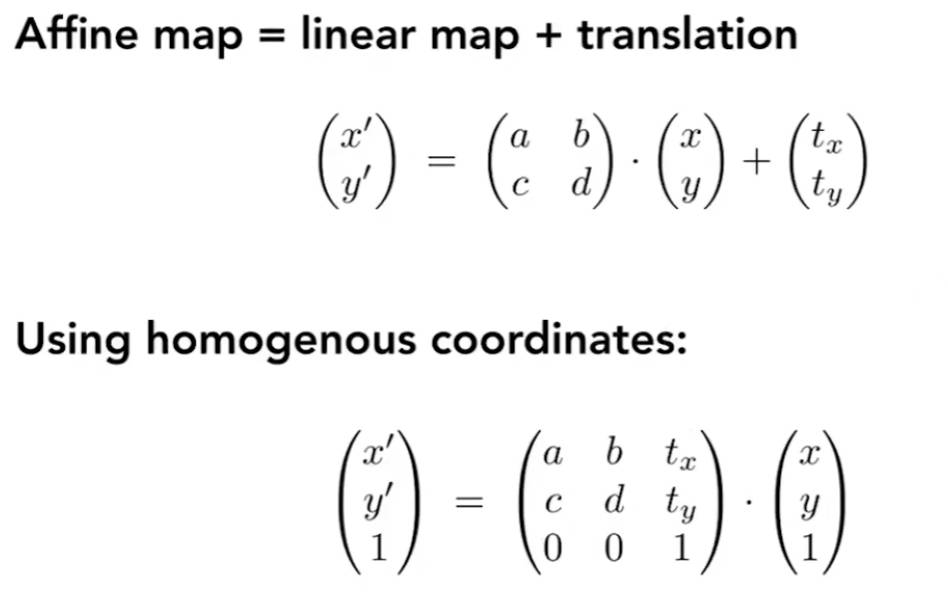
注意：整合到三维矩阵后，应该是先线性变换在平移

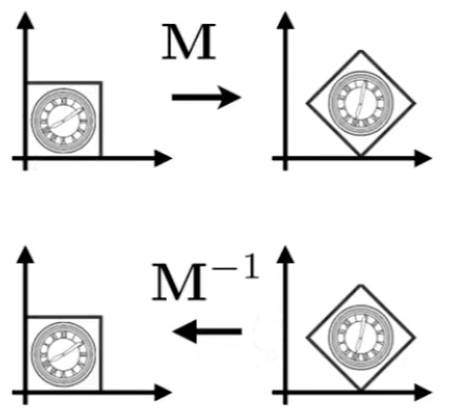
2.2.2 逆变换 Inverse Transform

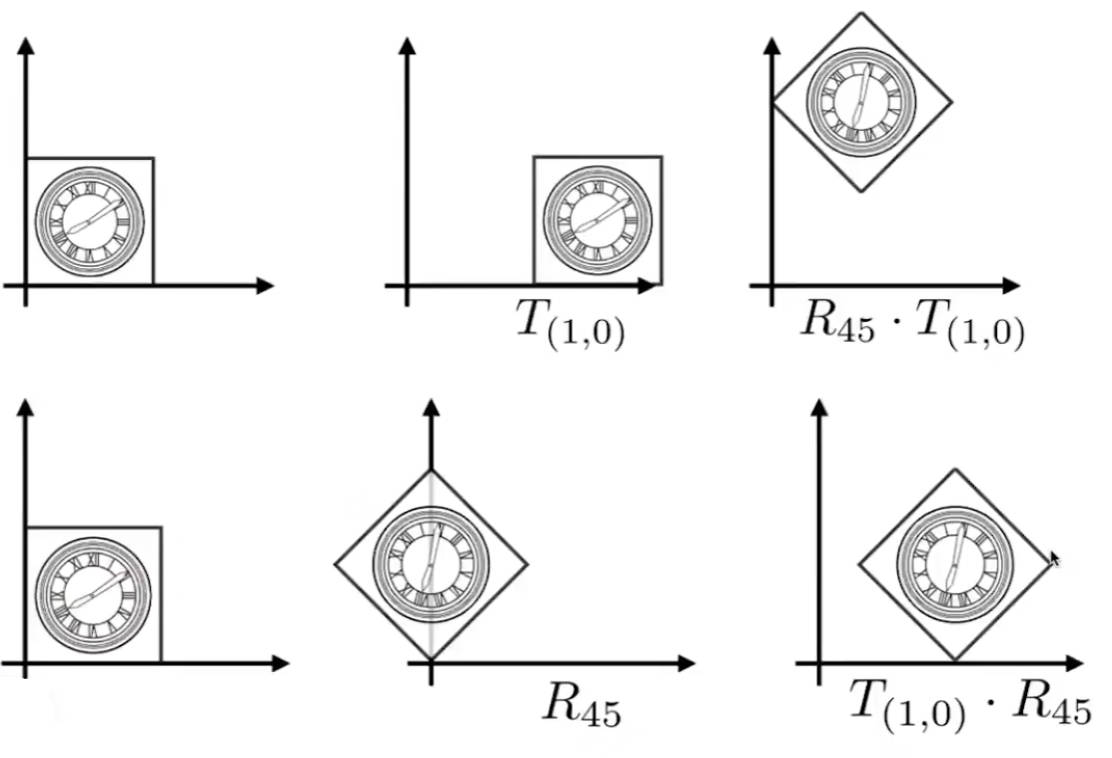
2.2.3 变换的组合

将变换分解为基本变换，然后根据先后顺序依次左乘（最先的在最右边）变换矩阵

2.2.4 三维变换

2.2.4.1 绕坐标轴旋转

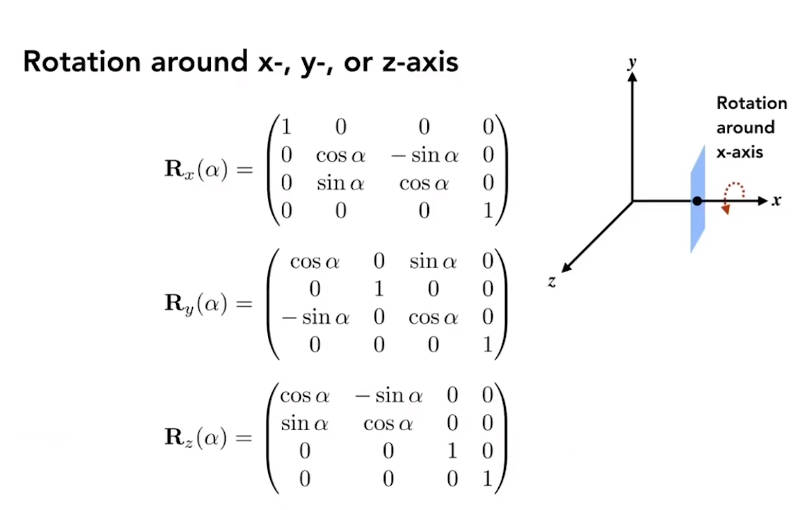
2.2.4.2 绕任意轴旋转

绕任意轴的旋转可以由绕三个坐标轴旋转的组合来表示。这三个旋转角度也叫欧拉角

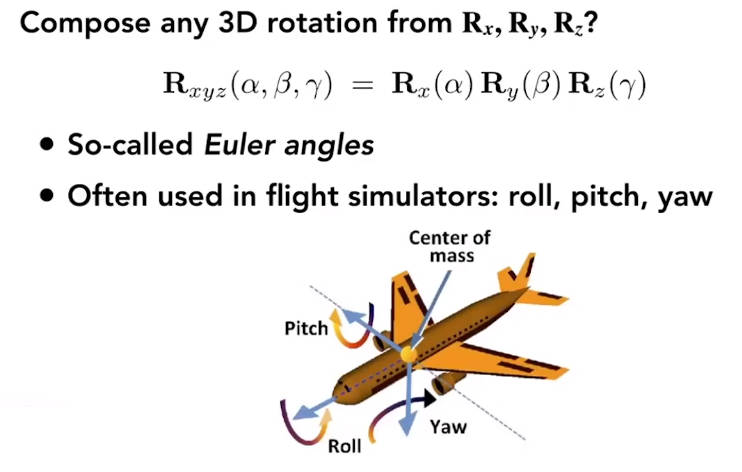
绕任意轴旋转也可以表示为绕单位向量 $n$ 旋转 $\alpha$ 角度

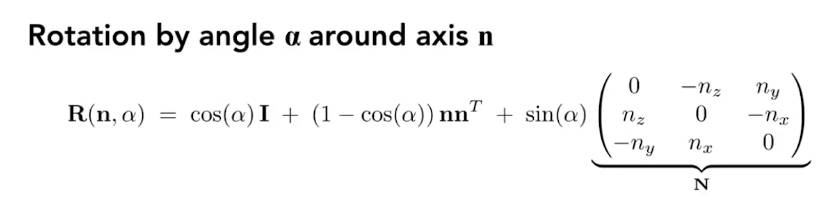
2.3 观测变换 Viewing transformation

拍摄一张照片，或者说将三维空间投影到二维平面的变换，叫做模型视图投影变换 model view projection（MVP）

2.3.1 视图变换 View/Camera transformation

以下是view视图矩阵的定义

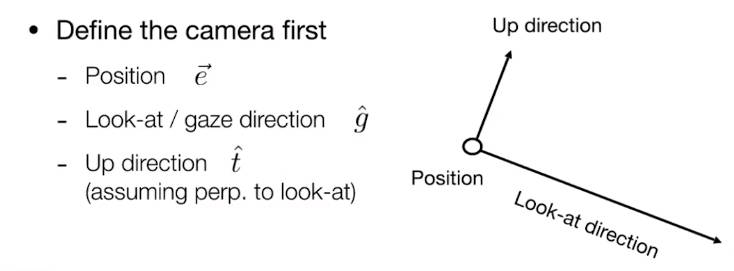
并做如下规定：

相机的位置始终在原点(0,0,0)
相机的拍摄方向始终朝 $-Z$ 方向
相机的向上方向始终朝 $Y$ 方向

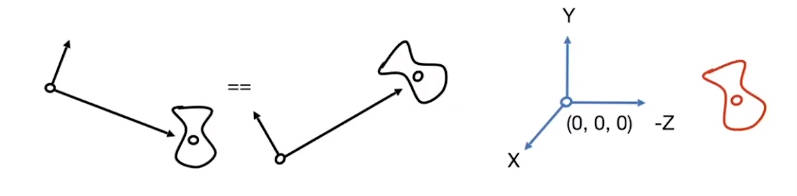
什么是view视图矩阵 $M_{view}$ ？就是原始相机通过这个变换矩阵 $M_{view}$ 之后会变换到刚才规定的状态

旋转矩阵是正交阵，也就是 $R^{-1}=R^T$

2.3.2 投影变换 Projection transformation

投影变换分为正交投影和透视投影。这两者的区别在于是否存在透视点。

以一个正方形为例子。在正交投影中，正方形的所有边都应该是平行或者垂直的，没有透视点。但是在透视投影中，正方形的边会指向一个透视点。

正交投影常用于工程视图中，而透视投影才是符合人眼看到的视图。

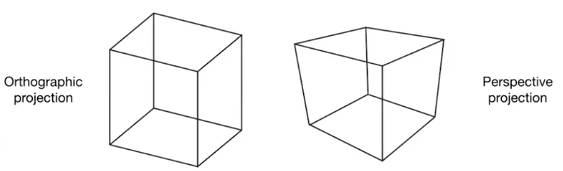
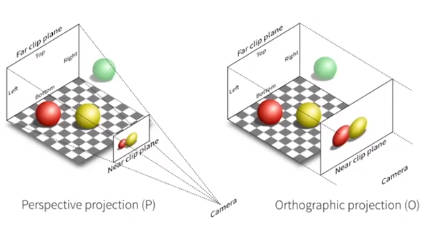
2.3.2.1 正交投影

对于正交投影来说，视野是一个矩形。

规定：将观测物体的中心移动到原点，并对物体进行缩放到 $[-1,1]^3$ 的范围内

正交投影矩阵就是将视野矩形变换到规定的状态

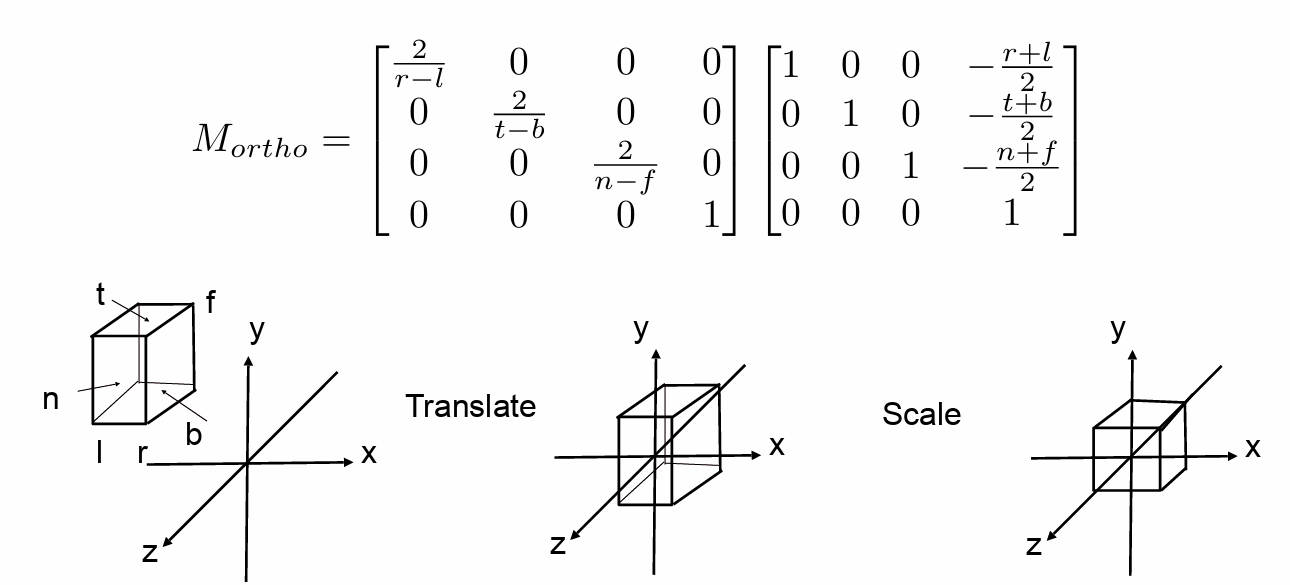
2.3.2.2 透视投影

透视投影的视野是一个锥形，且会在近平面成像。

透视投影分两个步骤：将视锥变换为矩形，然后做正交投影

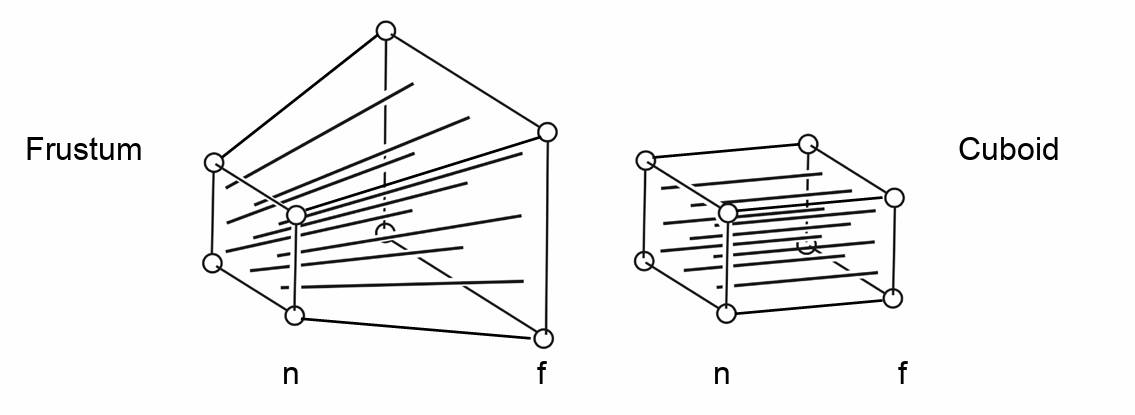
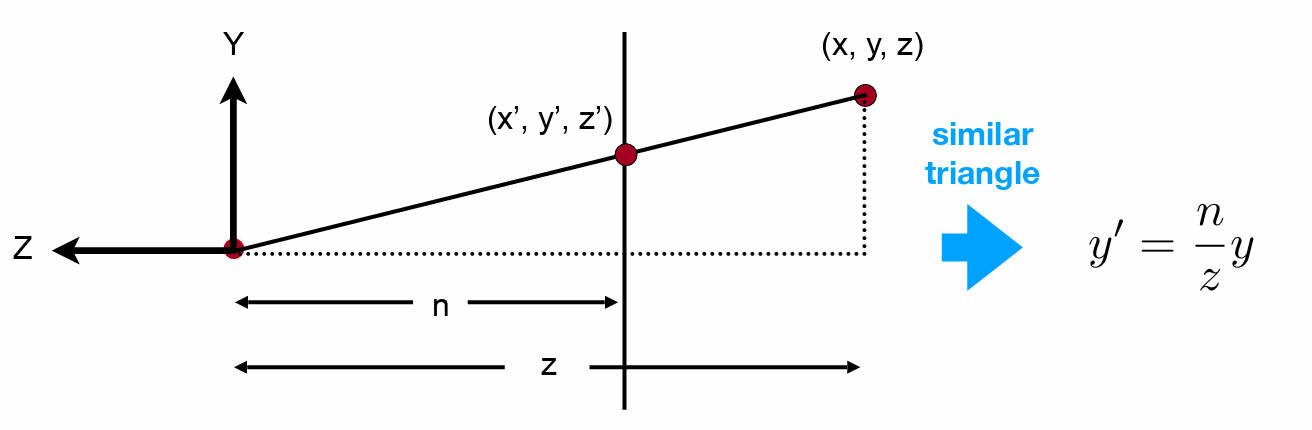
怎么将视锥变为矩形？对远平面在xy方向进行压缩，使其变为与近平面一样大。

怎么做？通过相似三角形改变xy的值：

变换矩阵怎么写？

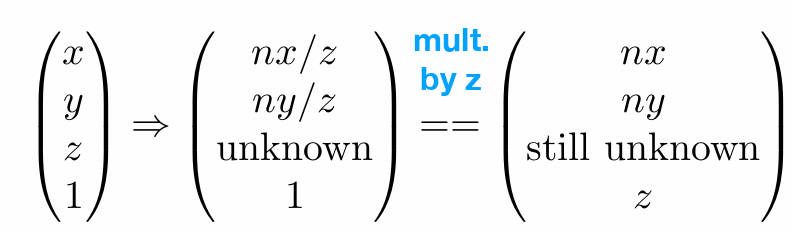
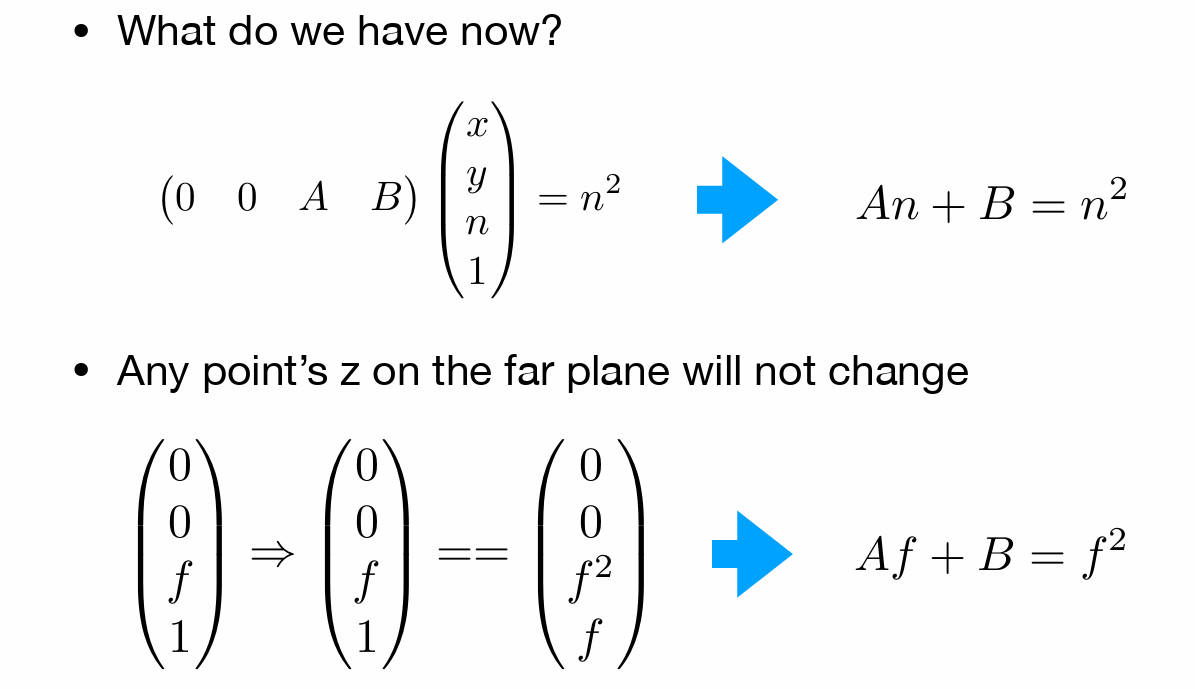
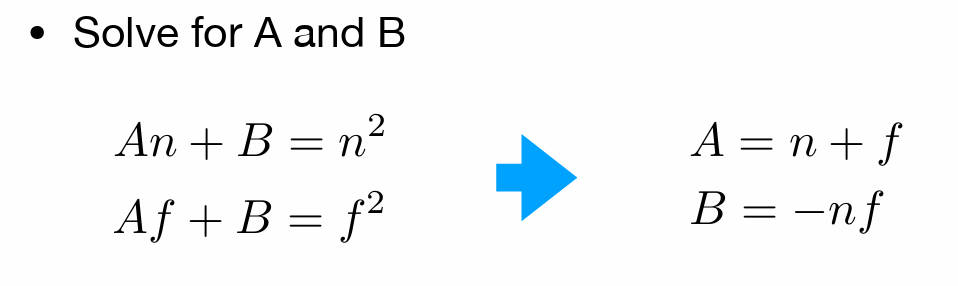
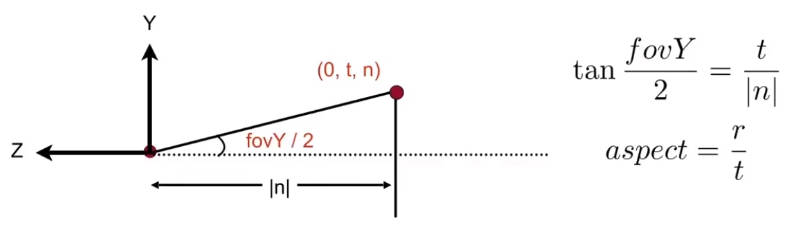
**怎么定义视锥？**通过视场fov（可视角度）和宽高比：（fovY也就是Y方向的可视角度）

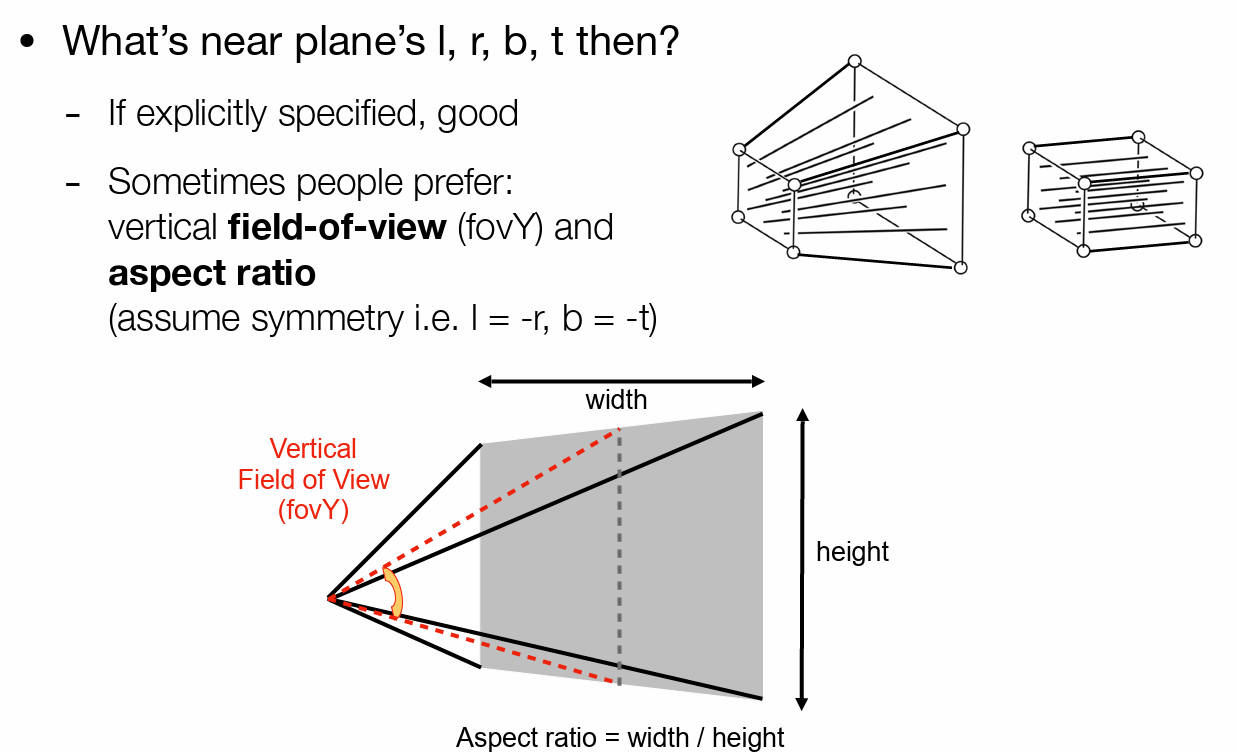
2.3.3 投影到成像平面

成像平面的大小取决于屏幕的大小或者规定图像的大小，也就是 $(width,height)$

因此需要将视野矩形 $[-1,1]^3$ 变换到 $[0,width]\times [0,height]\times [n,f]$ .（注意：规定屏幕的左上角是原点）

算上近平面和远平面的变换：

M_{viewport}= \begin{bmatrix} \frac{width}{2}&0&0&\frac{width}{2}\\ 0& \frac{height}{2}&0&\frac{height}{2}\\ 0&0&\frac{n-f}{2}&0\\ 0&0&\frac{n+f}{2}&0\\ \end{bmatrix}

2.3.4 如何理解MVP model view projection

$M_{mvp}=M_{projection}*M_{view}*M_{model}$

$M_{model}$ 是模型自身的变换矩阵

$M_{view}$ 是根据视点进行变换的矩阵，乘视图矩阵就是将视点和物体整体变换到一个指定坐标系下的指定位置

$M_{projection}$ 是再次将物体和视点进行了整体变换。视图矩阵是将视点变换到原点，投影矩阵是将视野矩阵的中心变换到原点，并将视野矩形变化到屏幕大小。 $M_{projection}=M_{viewport}*M_{ortho}*M_{pro\to ortho}$

最后怎么成像？根据z深度的值进行成像

3 三角形光栅化 Rasterization

光栅化 Rasterize = 将图像画在具有一组离散像素的屏幕上

3.1 三角形 - 基本形状单元 foundamental shape primitives

为什么是三角形？

最基本的多边形
- 任意多边形都可以拆分为多个多边形

三角形的性质：

三角形的内部一定在一个平面内
三角形的内外非常好判断 -> 使用向量叉乘
三角形内部点的像素值可以通过顶点的插值表示

3.2 如何在屏幕中画一个三角形

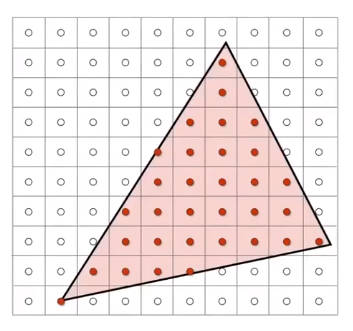
一种直观的方法是使用像素点中心坐标是否在三角形内部来判断，在内部则像素点置为1。

程序化表示为

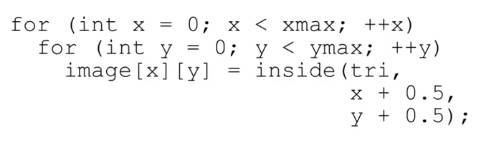
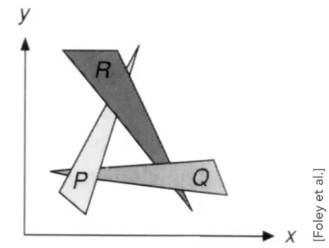
inside()函数的作用是判断像素点是否在三角形内部，函数的判断依据可以使用向量叉积的符号是否相同。

如下图所示。判断时，三角形的三边向量应该按照相同方向指定，即顺时针或逆时针。然后将三个顶点依次指向目标点。若目标点在三角形内部，那么由顶点指向目标点的向量始终位于边向量的同侧。即向量叉积的符号相同。

如果目标点在边上，则自己定义。

3.2.1 三角形的包围盒 Bounding Box

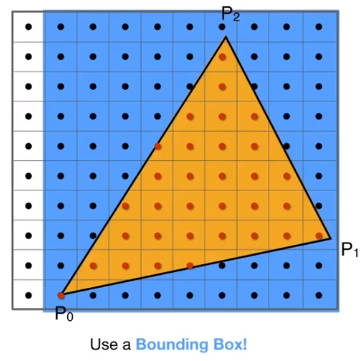
由三角形的三个顶点坐标划分出来的蓝色区域称为三角形的包围盒。也就是说只有在包围盒内部的像素点才参与三角形内外点的判断。

3.3 反走样抗锯齿 anti-aliasing

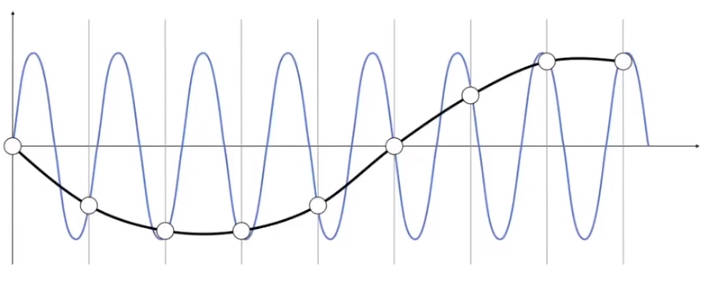
走样的定义：两个截然不同的信号用相同的采样方法会得到相同的采样信号。

如下图。蓝色和黑色是两种信号，使用空白点进行采样。采样出来的结果相同。

3.3.1 采样问题 Sampling Artifacts

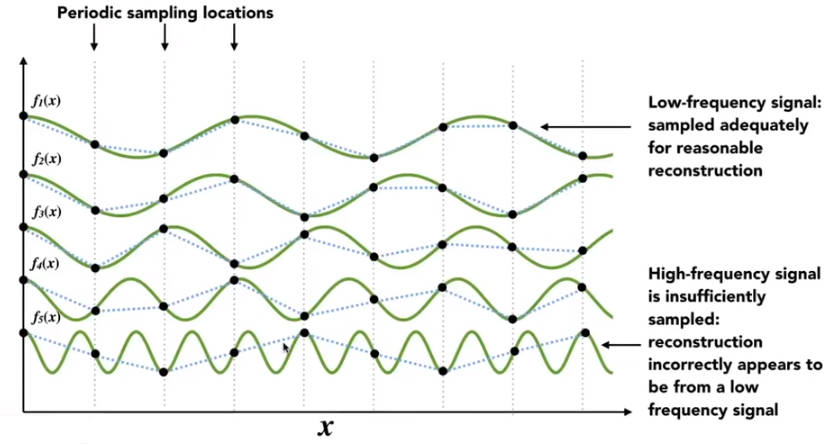
采样问题的本质的信号变化的频率太快了，但是采样的速度跟不上信号的变化.

相同的采样频率，随着信号的频率越高，虚线所表示的采样信号越不符合实际的信号。

3.3.1.1 锯齿 Jaggies

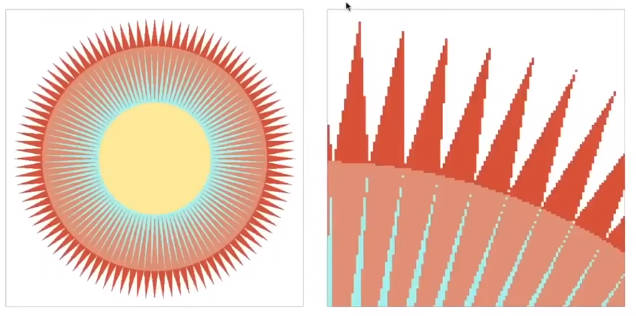
3.3.1.2 摩尔纹

3.3.1.3 车轮错觉

人眼观看快速旋转的车轮时会发现车轮倒转的现象。这是人眼在时间方面的错误采样

3.3.2 反走样的方法

在采样之前先对信号做模糊处理，也就是低通滤波。

回顾采样问题的本质：采样的频率跟不上信号变化的频率。

因此做低通滤波过滤掉高频信号，从本质上解决问题。

3.3.2.1 如何理解图像的高频信息

图像的高频信息一般是指物体的轮廓边界。

**轮廓为什么是高频的？**因为轮廓一般带有显著的像素值突变。

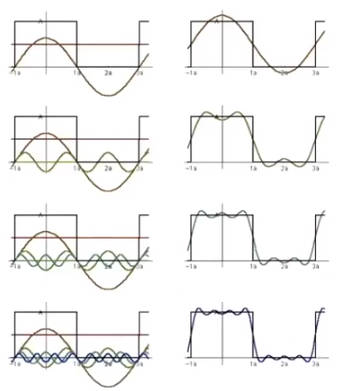
像素值突变可以类比为一个方波。如下图。用傅里叶变化来表示方波需要低频信号和高频信号的累加。

所以严格说，像素值突变是低频信号和高频信号的结合。

**如何来衡量像素点的高频程度？**使用梯度值

为什么傅里叶变换的频谱图总是会有一个十字线？

因为图像边界总是突变的，将图像重复上下左右铺开，会发现图像左边界和右边界往往是不连续的。

3.3.2.2 空域与频域的卷积

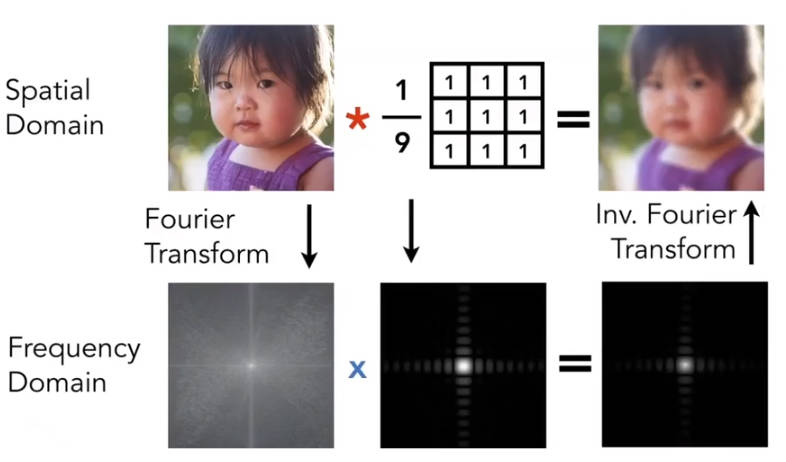
卷积核在空域和频域上的联系

右边可以理解为一个mask，只保留原频谱图中mask的部分

考虑两个极端情况：卷积核只有一个像素点大、卷积核和图像一样大

3.3.2.3 如何理解采样

采样就是在重复原始信号的频谱

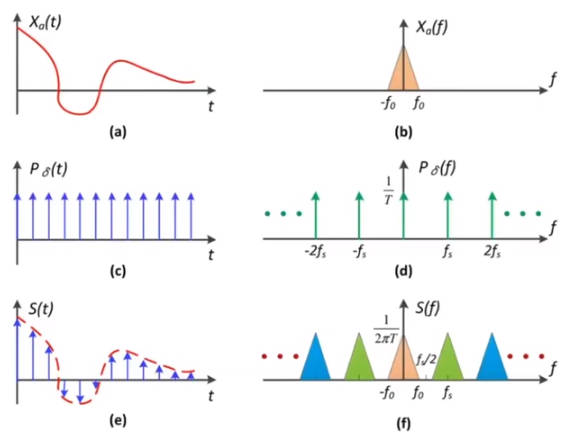
所谓走样，就是采样的频率跟不上信号的频率。反应到频谱中，就是采样信号的频谱发生了重叠。

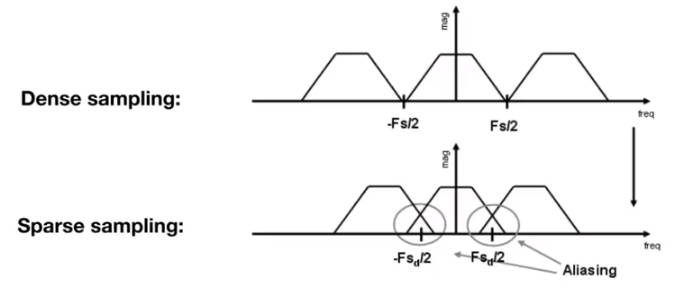
因此，反走样就是去除信号的高频部分。

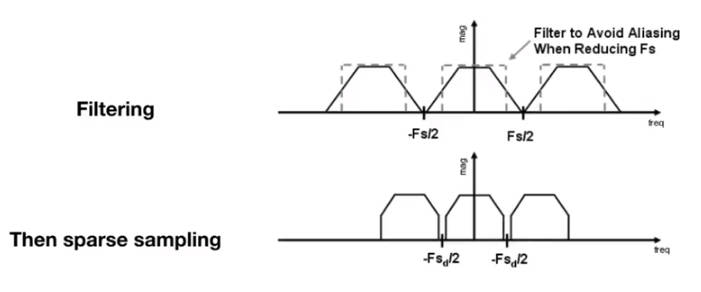
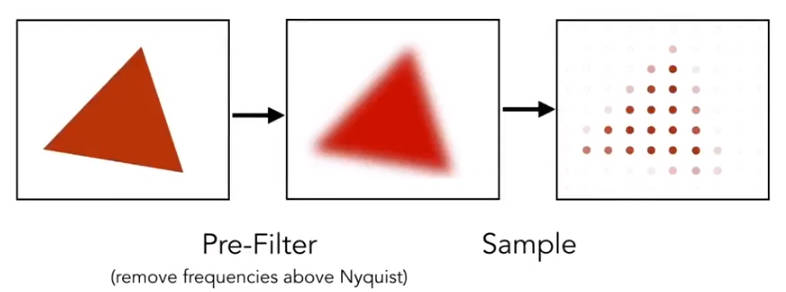
3.3.2.4 实际反走样的操作

3.3.2.4.1 SSAA（超采样反走样）

对一个像素值进行模糊处理，也就是平均化。下图中黑色部分是三角形内部的区域。

但是这样将一个像素当作连续空间来计算平均值太过消耗计算资源。

对一个像素值进行模糊处理，也就是平均化。

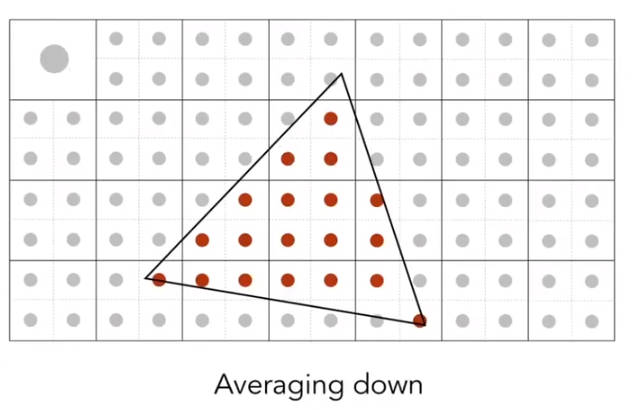
3.3.2.4.2 MSAA(多重采样反走样 Multisample anti aliasing)

为了降低计算消耗，将像素点分为多个小像素点（采样点）。也就是将一个像素点的连续空间离散化。

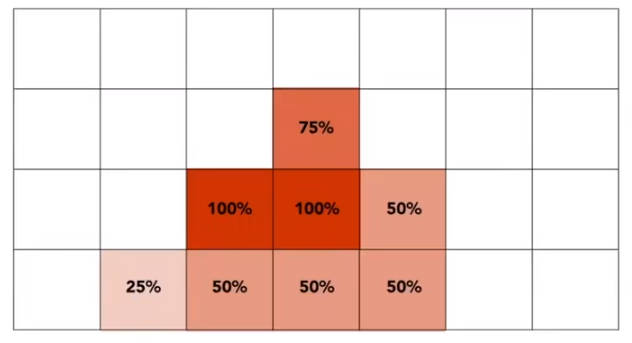
3.4 总结

抗锯齿方法的代价

成倍增加了计算量

除了MSAA外，另外里程碑的方法有：（GAMES104课程）

FXAA (Fast Approximate AA) 快速近似抗锯齿 -> 与增加样本数无关，是获得锯齿图像后的后处理。大致为，将图像渲染出来，然后边缘检测，对检测到的边缘进行模糊（Z-buffer？）
TAA (Temporal AA) 与图像匹配有关，将MSAA空域分布的采样点改为了时间上的分布，通过图像匹配将像素时间上的改变联系起来，然后进行量化。也就是前一帧的像素值会影响后一帧的像素值。类似视觉暂留。

超分辨率问题

4 着色 Shading

4.1 画家算法

画家算法是先渲染远处的物体，在依次渲染近处的物体，最后完整的画出图像。

4.2 深度缓存 Z-buffer

当场景中物体的深度关系比较复杂时，画家算法处理起来就会很麻烦。（顶点可见性判断时目前最通用的算法？）

为了处理这种情况，Z-buffer将每个像素作为对象，同时生成两张图。一张表示当前像素的深度，一张表示像素的颜色信息。右图中，颜色越深说明深度越小。

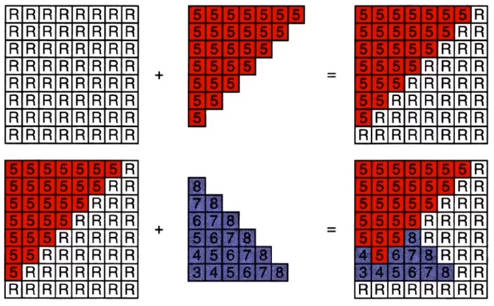
时间复杂度的比较

画家算法需要对同一个的像素点位置的不同像素点深度进行排序，所以是O(n*log n)

Z-buffer只需要像素点深度最小的值，所以是O(n)

Z-buffer的性质：渲染时对图像中同一坐标的不同深度的像素点是没有渲染的先后顺序，因为最后肯定是深度最小的像素点。因为这种无序性，Z-buffer可以部署到GPU上。

Z-buffer一定处理不了透明物体

4.3 一个简单的着色模型-冯氏反射模型 (Blinn-Phong Reflectance Model)

变量定义：

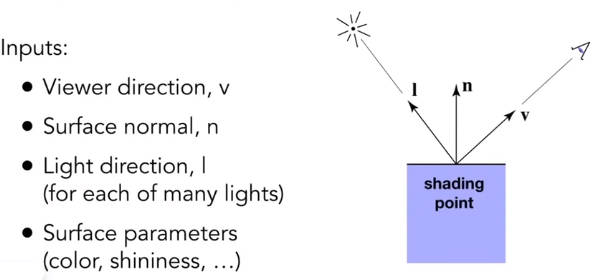
着色是局部的，只考虑颜色、光照的反射，不考虑阴影。（表面的明暗变化不等于阴影）

4.3.1 漫反射 Diffuse Term

反射回来的光均匀分布在任意方向。有就是说漫反射的表面颜色在任意方向看都是一样的。

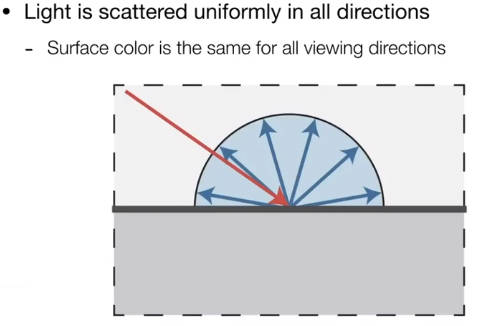
4.3.1.1 光的接收

物体表面接收光的能量与光线方向和表面法线的夹角的余弦值成正比。

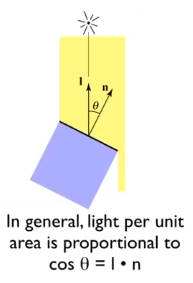
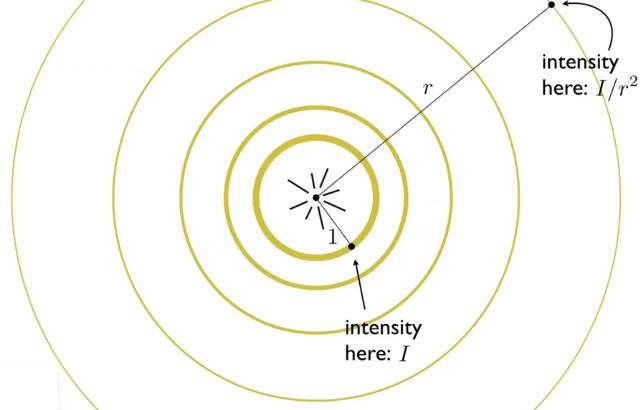
4.3.1.2 光的传播

点光源向外传播的能量可以看作是一圈一圈的球壳。能量均匀分布在球壳上。球壳随半径扩大，但是能量总值不变。所以能量与半径r的平方成反比。

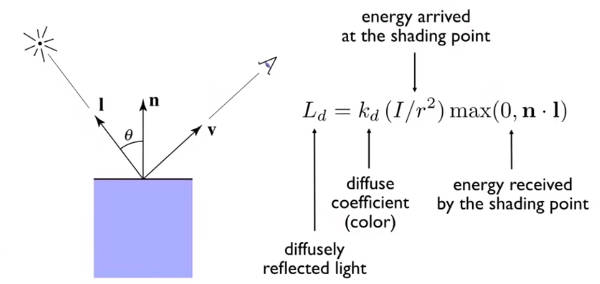
4.3.1.3 漫反射公式

漫反射的着色独立于观测视角

单位向量n与l点乘表示 $cos(\theta)$ ，当为负值时，说明光线从物体表面之下照射过来，所以令其为零。

$k_d$ 表示物体表面吸收能量的程度，为1则是不吸收，那么是最亮的，为0则是全吸收，是最暗的。如果是一个rgb三通道向量，则表示出了物体表面吸收rbg的程度。

4.3.2 高光 Specular Term

高光依赖于观测方向

如果观测向量v和反射向量R接近，则会看到高光。

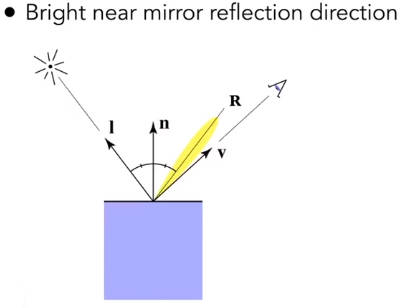
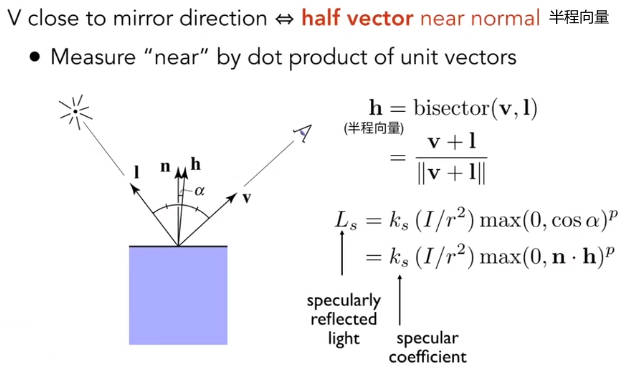
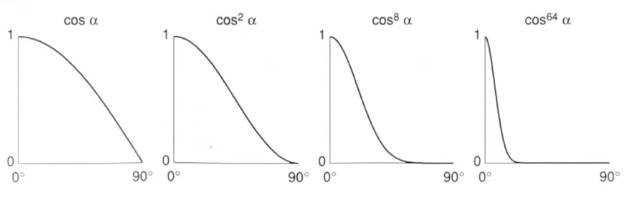
注意公式中存在一个指数p，这反映了对夹角 $\alpha$ 的容忍度。

从下图可以看出，不加指数的话，夹角到90°才不会看到高光，这明显不符合常识。因此，模型中常将指数p设为100到200.

4.3.3 环境光 Ambient Term

这个模型将环境光视为一个常数，与任何向量都无关。

4.3.4 完整的冯氏反射模型

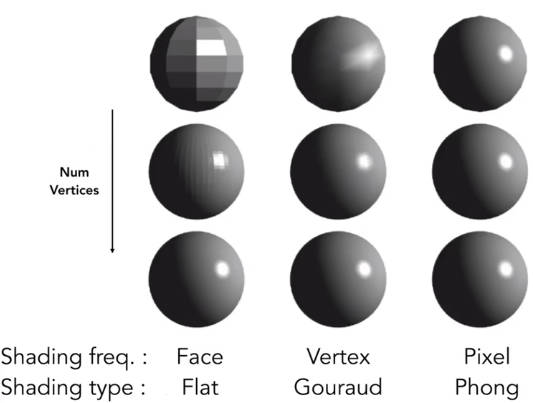
4.4 着色频率

下图中。左边的图，着色应用在三角形的面。中间的图，着色应用在平面的顶点，对顶点进行插值来填充平面。右边的图，着色应用在每个像素上。

4.4.1 平面着色 Flat shading

4.4.2 顶点着色（高洛德着色）Gouraud shading

4.4.3 像素着色 Phong shading

4.4.4 着色频率的两个问题

4.4.4.1 怎么知道逐顶点着色的顶点法线是什么

平面的顶点是多个三角形平面的交点，于是一个简单的方法就是将与顶点相邻的所有平面的法向量求平均，就得到顶点的法向量了。改进就是加权平均。

4.4.4.2 怎么知道逐像素着色的像素法线是什么

计算顶点法线后通过插值来计算像素法线。常用重心插值（barycentric interpolation）

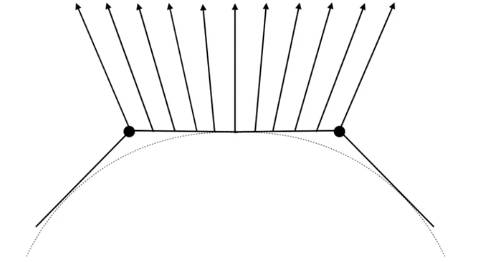
4.5 图像管线\实时渲染管线 Graphics Pipeline

着色器编写网站：Shadertoy BETA

Shader 的水非常深！！！

4.6 纹理映射 Texture map

对于同一个着色模型，不同物体会有不同的颜色，这件事本质上是因为物体的漫反射系数不同，再进一步说就是物体的纹理不同。一个物体本身的不同区域的纹理也会不同。因此，纹理映射是想将一个物体的纹理表示出来。

下图就是将一个物体展开成一个平面，这个平面是有一个纹理坐标系表示，坐标轴为 $(u,v)$ ，取值在[0, 1]。坐标中的颜色表示漫反射系数的值。坐标系中的每一个点也叫纹素

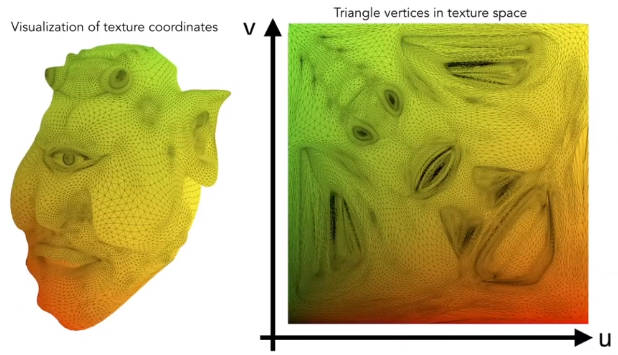
另一个纹理映射的例子

虽然在纹理坐标系下，每块之间的纹理不是连续的，但是在实际渲染中看不出来。这取决于纹理的设计，要四方连续，无缝贴图。（Wang Tilling还是undecidable的，关于Veritasium的视频）

4.6.1 纹理映射存在的问题

4.6.1.1 纹理放大

直观理解就是低分辨率的图放到高分辨率的屏幕中，会出现模糊。

解决方法，插值。最近邻插值、双线性插值、双三次插值

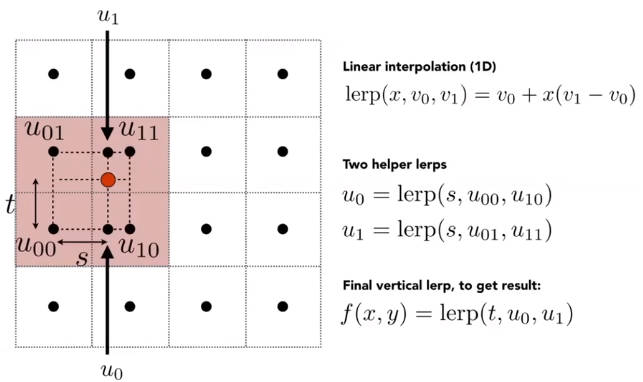
双次线性插值

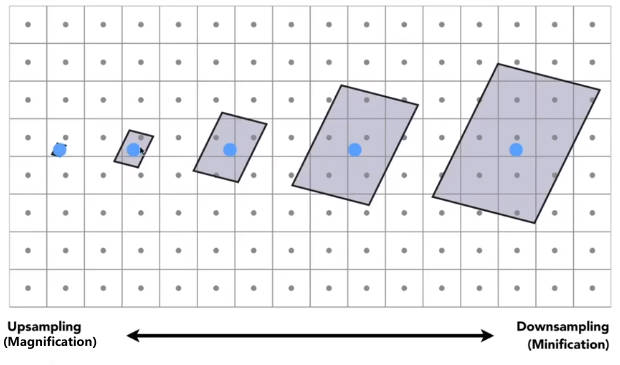
4.6.1.2 纹理太大或者说纹理太细

纹理太密集，再使用之前提到的渲染管线、重心插值，则会出现摩尔纹

出现的原因：一个像素覆盖了多个纹素（纹理表达的单位），多个纹素求平均得到一个像素的纹素，这显然有问题。

4.6.1.2.1 三线性插值 Mipmap

这就好像是先模糊再采样，还是先采样再模糊，见3.3.2.3节。因此这个问题出现的原因可以理解为现在纹素坐标系进行了采样，再在像素坐标系进行了模糊，这显然不如先模糊再采样。那么应该怎么先模糊呢，那就是在纹素坐标系进行模糊处理，但是在一张图中，由于透视原因，一个像素点包含的纹素个数是不固定的，因此，纹素的模糊程度也是不固定的。所以要使用图像金字塔（Mipmap）来存储不同程度模糊的纹素信息。这属于点查询问题和区域查询问题。

如何快速计算某一个像素点对于的纹素模糊程度呢？通过像素点覆盖的纹素区域的大小来判断。

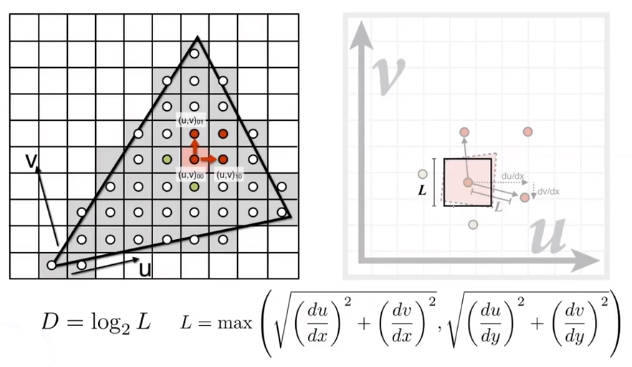
D是Mipmap的下采样层数.

下图是纹素模糊程度的可视化，也就是不同下采样层数（D）对应的位置。可以看出这个变化是不连续的。

这有两个原因，一是L可能不是2的次数，比如L可能是3。二是纹素本身也是离散的，所以像素点对应到纹素图中也需要插值。

这两个问题解决方法都是插值。问题一使用层与层之间的插值。问题二使用纹素点之间的插值。

这个方法称为三线性插值 Trilinear Interpolation

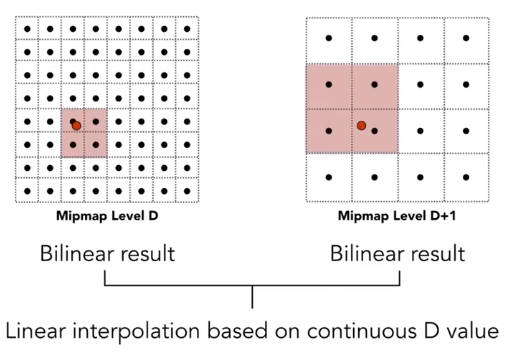
但是Mipmap 三线性插值存在过度模糊的问题。问题在于Mipmap只能查询一个正方形的区域，将像素区域进行了正方形的近似。

4.6.1.2.2 各向异性过滤 Ripmap

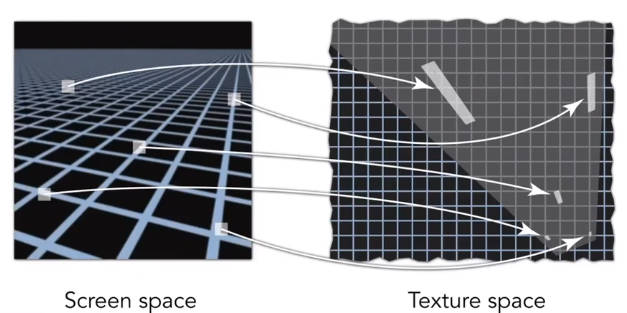
Ripmap保留了横向和纵向的不同程度的缩小。这使得映射回原始纹素图时，映射的区域不局限为正方形。

如下图。各向异性过滤可以处理矩形的映射区域，但是对斜着的矩形区域没有办法处理。显存的开销是原来的三倍。

4.6.1.2.3 其他方法（？）

4.6.2 纹理映射的应用

4.6.2.1 环境映射

将环境光作为纹理来存储在球上。但是存储在球上，再展开是会发生扭曲。

犹他壶

4.6.2.2 凹凸贴图/法线贴图

通过将纹素设为像素点的虚拟高度值，从而修改像素点的法线方向。

具体来说，现在纹素值是虚拟高度dp。对于二维平面来说，这个虚拟高度指的是该点向右移动一个单位会上升的高度。

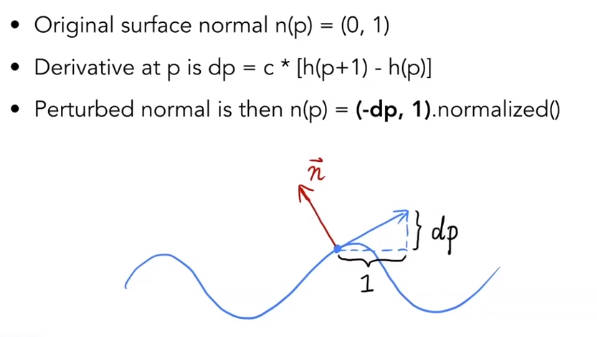
在三维空间中这写为：

只是贴图，所以球面没有真的进行形状改变。

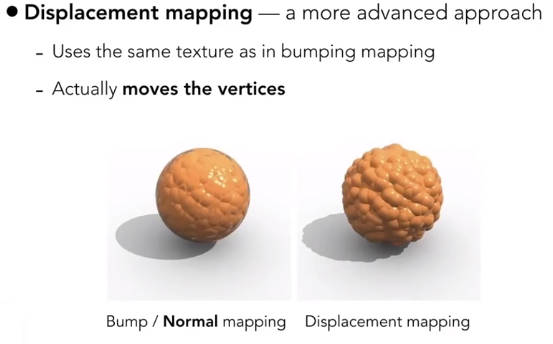
4.6.2.3 位移贴图

改变三角形的顶点位置。但是会大量增加三角形个数。使用了曲面细分技术，自适应的增加三角形个数。（DirectX）

4.6.2.4 3D泊松噪声 + 立体模型

定义三维空间的噪声函数，通过二值化之类的操作，来建立三维模型。（Diffusion？）

4.6.2.5 存储已经计算好的着色信息

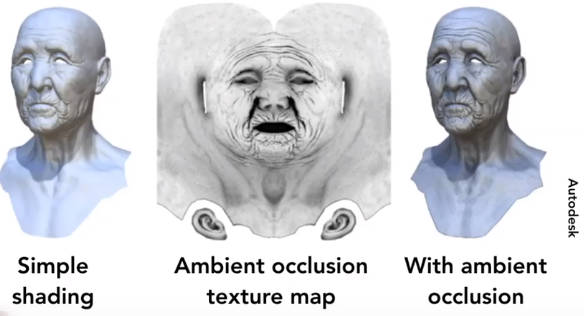
4.6.2.6 体渲染

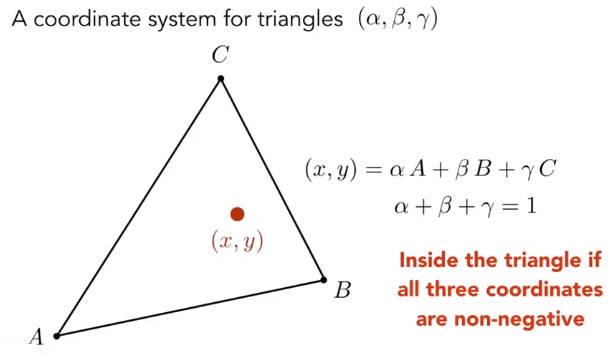
4.7 重心插值

无论是像素法线和像素纹理都需要根据三角形的顶点进行插值，常用的方法是重心插值。

三角形所表示的平面内的任意一点，都可以由三角形的三个顶点的线性组合来表示。因此使用 $(\alpha,\beta,\gamma)$ 在三角形坐标系中表示任意一个点。 $(\alpha,\beta,\gamma)$ 称为重心坐标

如果点在三角形内，则 $(\alpha,\beta,\gamma)$ 都是非负的。

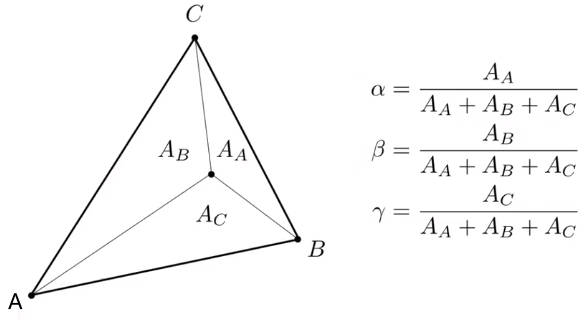
重心坐标的计算公式如下：

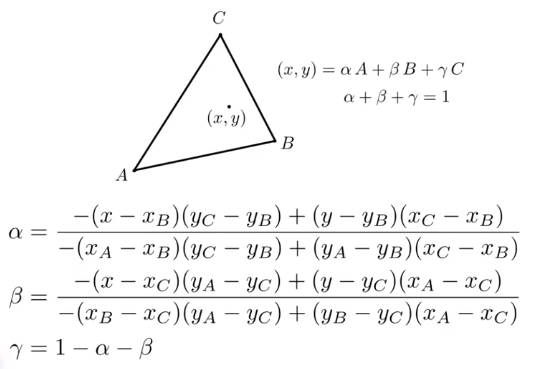
三角形自身的重心的定义是，存在一个点，使得划分后的三个三角形的面积相等，则

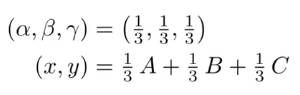
因此，重心插值就可以使用重心坐标来线性表示

需要注意的是，重心坐标不具有投影不变性，也就是说三角形经过投影变换后，点的重心坐标会发生改变。因此，重心插值应该在三维空间中进行，而不是投影之后的平面。

5 几何

几何的表示可以分为隐式和显式。

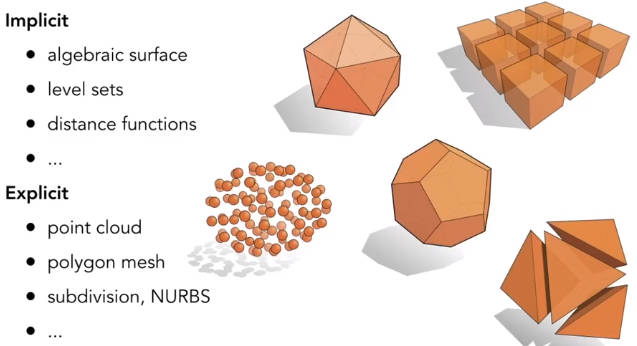
5.1 隐式表示的概述

简单的说，就是说不告诉点的具体位置，而是用函数之类的方式来表示。优点是非常容易判断点是否在模型内。缺点是无法直观了解模型的形状。

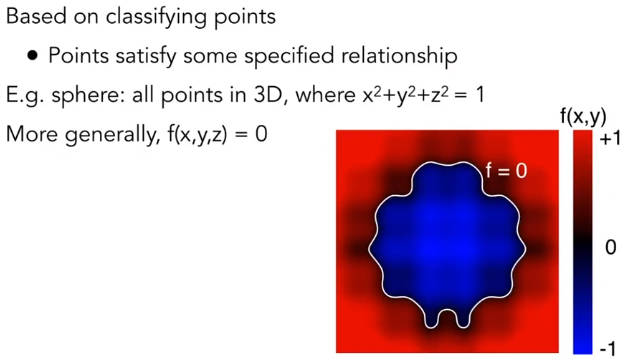
5.1.1 水平集 level set

通常用来做融合或者切片

5.2 显式表示的概述

直接通过三角形渲染或者是其他空间点的参数映射关系。

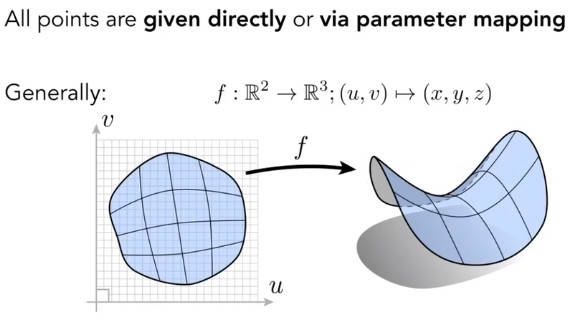
5.2.1 点云

5.2.2 多边形面

如何具体用三角形来表示三维模型？使用Wavefront Object File (.obj) 文本文件

下图实例是描述的一个立方体。

v 是顶点坐标，共八个点
vn是表面的法线，共六个面
vt是纹理坐标，对应的顶点
f表示三角形面的组成，也就是顶点的链接关系，格式为v/vt/vn的索引

5.3 贝塞尔曲线 Bezier Curve

通过多个控制点和切线来画出曲线。

5.3.1 如何画贝塞尔曲线 de Casteljau Algorithm

以三个控制点为例。将控制点依次连线，然后给定参数t，将线段按 t:1-t 的比例划分。划分处得到新的控制点，将新的控制点连线，按同样比例划分得到新的控制点。不断迭代，直到只剩一个控制点。从而由该控制点和首尾两点确定一条曲线。

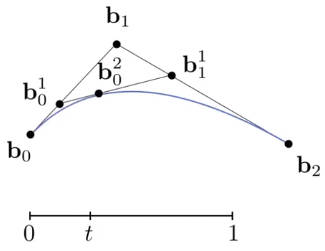
当t作为时间连续时，不同的时间可以画出同一条贝塞尔曲线上不同的点。

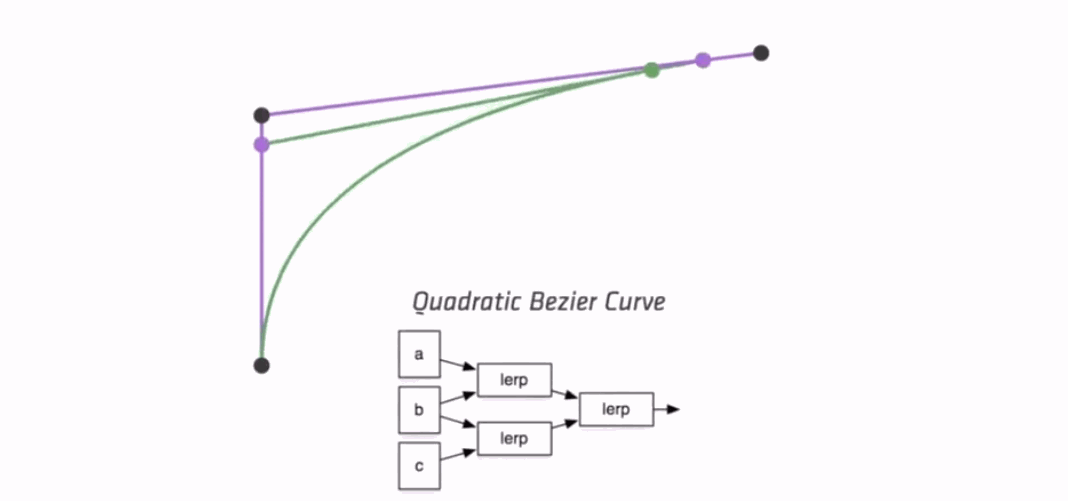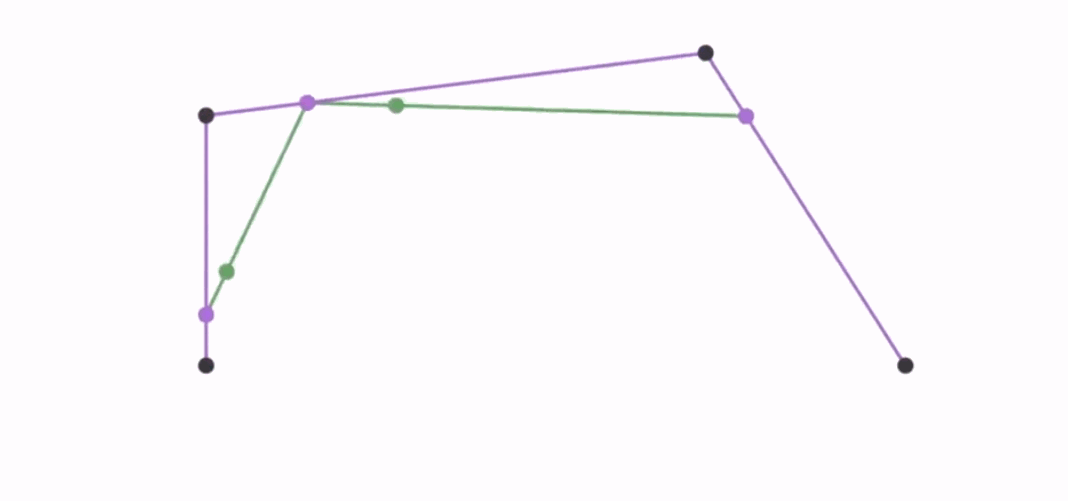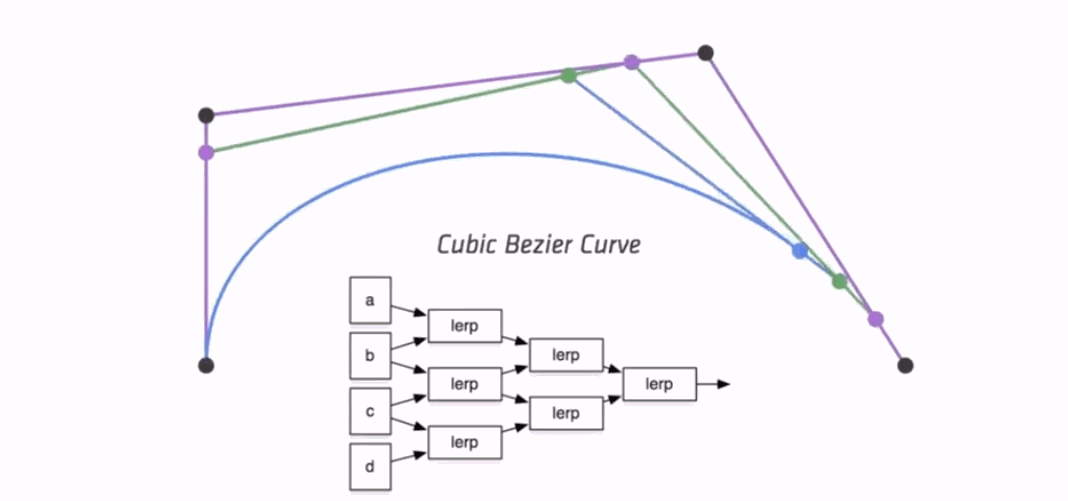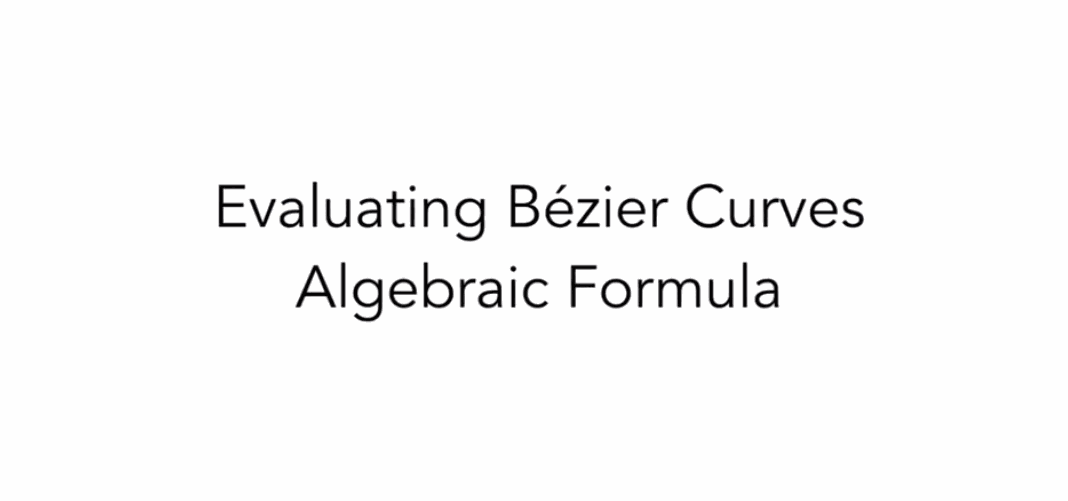
5.3.2 贝塞尔曲线的显式公式

贝塞尔曲线上的点可以看作是给定控制点的线性组合。

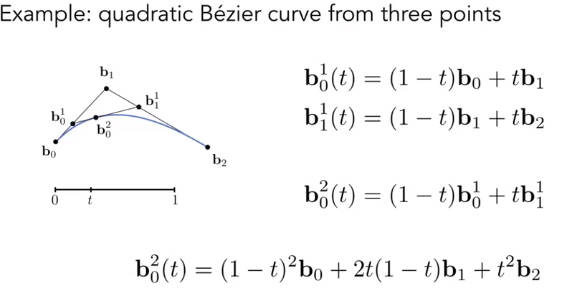
给定从0到n，共n + 1个控制点，贝塞尔曲线上的点可以如下表示：

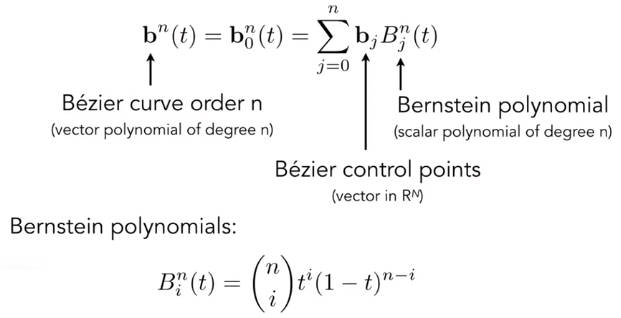
伯恩斯坦多项式Bernstein polynomials 描述的是一个二项分布。 $\bigg( \begin{matrix} n \\ i\end{matrix} \bigg)$ 是 $C_n^i$ 的一种写法

为什么是二项分布？

观察三个控制点的例子，t是在[0, 1]区间，系数是t 和 1 - t 的组合，恰好满足二项分布的性质。

**贝塞尔曲线不只是局限在二维平面。**在三维空间甚至多维空间中也可以画，控制点的坐标是几维，贝塞尔曲线就是几维。

5.3.3 贝塞尔曲线的性质

贝塞尔曲线一定过起点和终点
对贝塞尔曲线做仿射变换，可以通过对控制点做仿射变换，用变换后的控制点画出来的贝塞尔曲线就是仿射变换后的贝塞尔曲线。
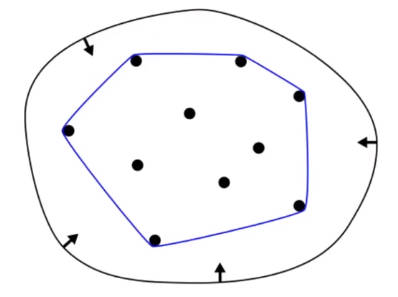
凸包性质，曲线一定在控制点所划分的凸包内。

如何理解凸包？将下图中的黑点可以看作是控制点，也可以看作是木板上的钉子，现在将一个拉伸后的橡皮筋放到木板上，然后松手。橡皮筋收缩并会被最外围的一圈钉子挡住，形成一个凸多边形，这个凸多边形就是凸包，且贝塞尔曲线一定在凸包内。

5.3.4 逐段贝塞尔曲线 Piecewise Bezier Curves

曲线越长，根据其变化程度可能需要更多的控制点，并且更难控制。如下图

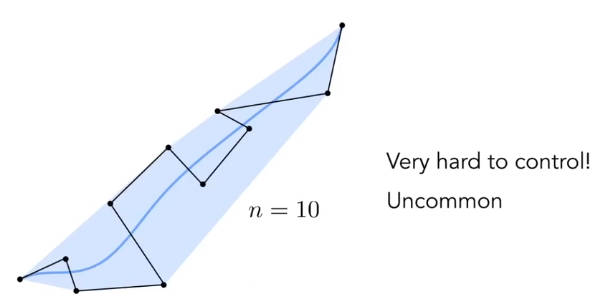
为了解决这个问题，Piecewise Bezier Curves将曲线分段，划分标准是每段可以由四个控制点形成。

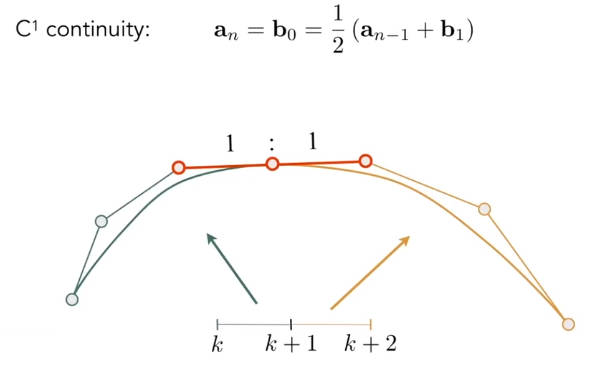
分段之后出现一个问题，那就是怎么保证在分段处曲线是光滑的（一阶可导）？

分段处的点一定是起始点也是终点，因此它的前后一定各有一个控制点。分段点分别与这两个点连线，若这两条线段梯度相同且大小相等，则分段处连续。

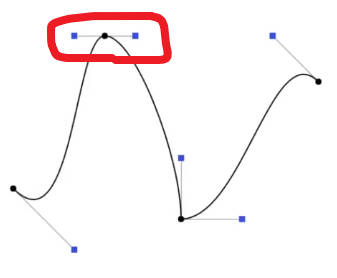
连续分为 $C^0$ 连续和 $C^1$ 连续。 $C^0$ 连续是起始点与终点重合，也就是 $a_n=b_0$ 。 $C^1$ 连续见下图，也就是刚才提高的一阶可导。

5.3.5 B样条曲线

13-7-2B样条曲线曲面第一节_哔哩哔哩_bilibili

5.3.6 贝塞尔曲面

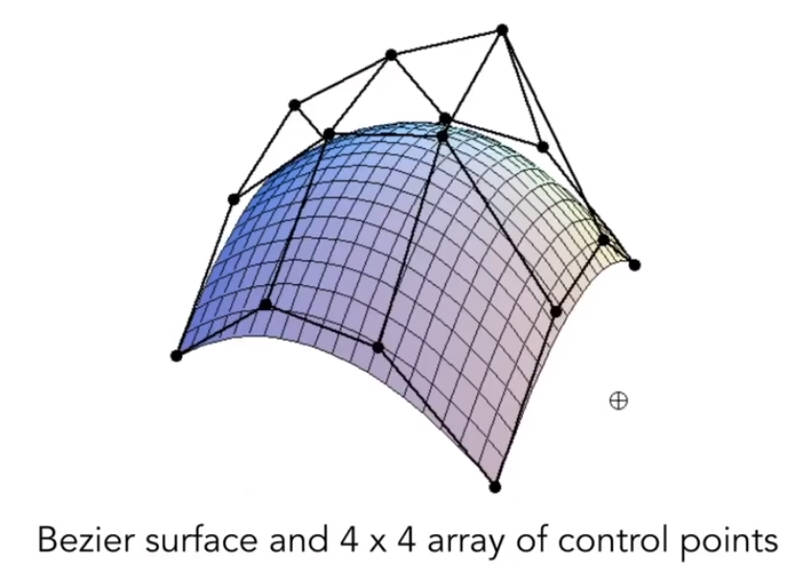
一个贝塞尔曲面通常由4 x 4共16个控制点组成。首先每行的4个控制点形成一个贝塞尔曲线，共4条贝塞尔曲线。然后在四条贝塞尔曲线中选取四个点作为纵向的贝塞尔曲线的控制点。通过时间t的改变，纵向的扫描整个曲面，形成贝塞尔曲面。类似插值的想法。因此贝塞尔曲面上的点可以通过两个参数来表示，分别是横向曲线的时间和纵向曲线的时间，即 $(u,v)$

贝塞尔曲面

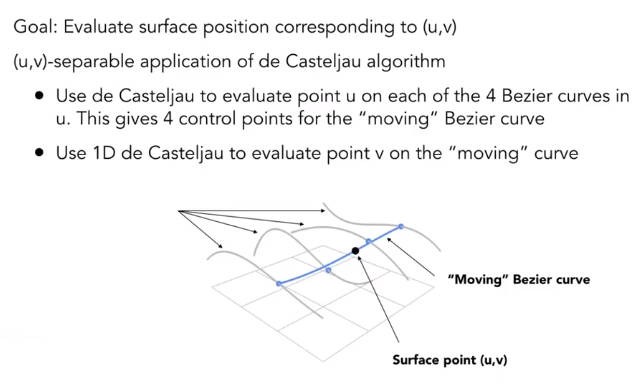
5.4 对于三角形的网格操作：几何处理

网格细分
网格简化
网格正则化

5.4.1 网格细分

5.4.1.1 卢氏细分 Loop Subdivision（不是循环的意思，作者姓Loop）

5.4.1.1.1 生成新顶点

第一步，生成新的顶点。生成依据是，选取原来的三角形网格的边的中点。三个边的中点连接，将一个三角形网格划分为了4个三角形网格。

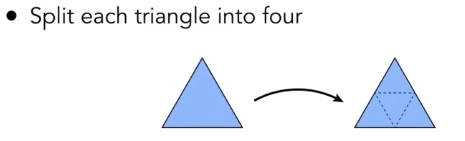
5.4.1.1.2 调整新顶点的空间位置

卢氏循环将顶点区分为旧顶点和新顶点。旧顶点是初始三角形网格的顶点，新顶点是根据边中点生成的顶点。

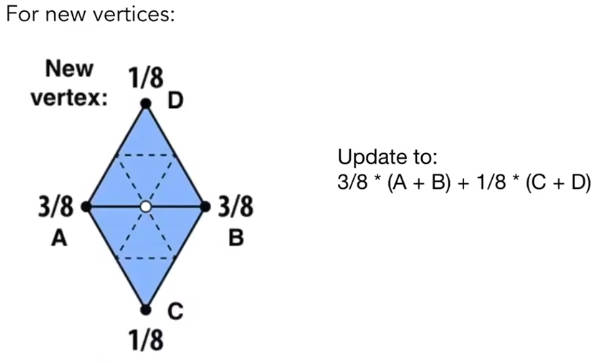
第二步，根据旧顶点的位置，调整新顶点的空间位置。具体见下图。这是一种加权平均。白点是新顶点，将相邻的旧顶点的权重设的相对大一些，不相邻的权重小一些。还有更复杂的情况，比如新顶点不止两个相邻点。

这个权重是人为设定的，AB中点是1/2(A+B)。CD中点是1/2(C+D)，再对这俩中点加权平均，权重为3/4和1/4（黄金比例？）。

加权平均也是平均，平均意味着平滑。通过加权平均来调整点的位置，实际上就是对空间面进行贫化。

5.4.1.1.3 调整旧顶点的空间位置

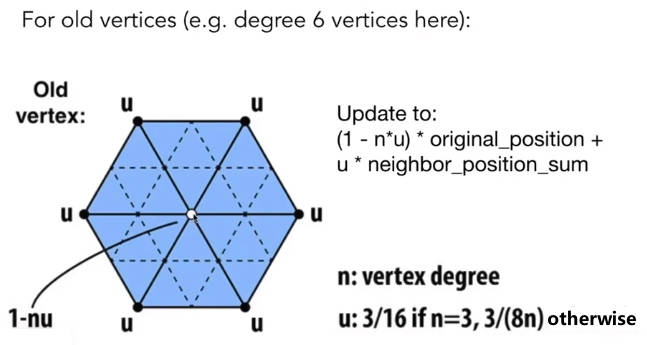
第三步，根据旧顶点相邻的旧顶点，加权平均旧顶点的空间位置。因为白色旧顶点本身也是旧顶点，需要保留自身的信息，所以将白色旧顶点的权重设为 $(1-n*u)$ ，其他相邻旧顶点权重设为 $u$ 。其中 $n$ 是点的度，也就是该点的相邻点的个数。 $u$ 是相邻点的权重，在 $n=3时，u=3/16，其他情况u=3/(8n)$ .

这个加权说明，度越小，白色顶点越重要，就越要保留原本的信息。

5.4.1.2 Catmull-Clark Subdivision (General Mesh)

Catmull-Clark Subdivision可以用于各种面，而不局限于三角形面。而Loop Subdivision则只能处理三角形面。

Catmull-Clark Subdivision做了两个定义：

所有不是由四边形组成的面都称为非四边形面
所有度不是4的顶点都是奇异点

Catmull-Clark Subdivision细分的两个步骤：

在所有面上选取一个点（可以是重心、中心等等，因为之后还要调整，所以随便）
在所有边上标上中点，并将新顶点连线

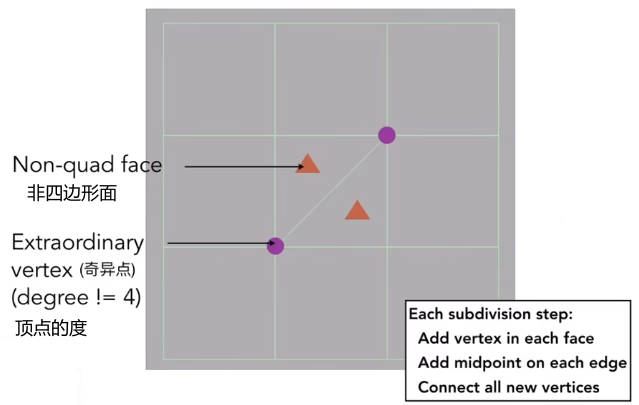
Catmull-Clark Subdivision在做第一次细分时，所有非四边形面都会消失，并增加消失的非四边形面的个数的奇异点。只在第一次细分时会有这样的情况。

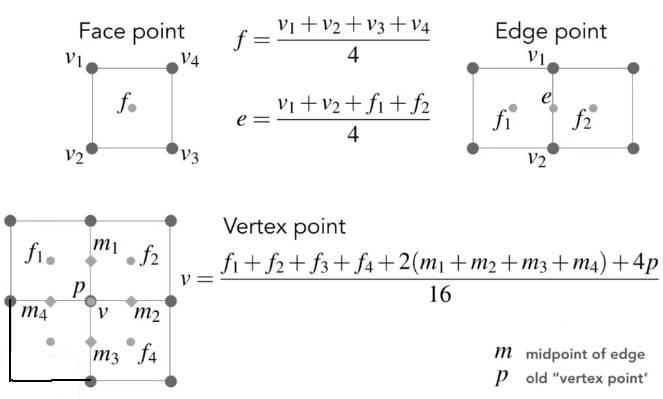
Catmull-Clark Subdivision顶点的调整策略见下图：

5.4.2 网格简化

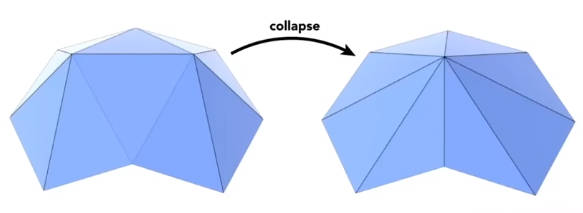
5.4.2.1 边坍缩 Collapsing An Edge

5.4.2.1.1 二次误差度量

边坍缩就是将一条边去除，将这条边上的两点合并为一个点。

那么合并后的点的位置怎么确定？

如果只是简单的取原始点平均，合并点永远不符合原始轮廓。见左图，紫色的三角形的面积永远比灰色多边形的面积小。

于是提出了二次误差度量。现在给定一个合并点，要使这个合并点到与其相关的所有平面的距离的平方和最小。

相关平面是什么？就是所有参与这次坍缩的原始平面。

但是出现了一个新的问题，坍缩哪条边可以使得原始轮廓变化最小？这需要计算每条边坍缩后的合并点的二次度量误差，将二次度量误差作为边的权值，选择权值最小的进行坍缩。

于是又出现一个问题，一条边坍缩之后，相关平面都会重新生成，那么相关边的权重又会发生变化。为了解决这个问题，需要进行两个操作：

第一，从一堆边中选取最小的权重进行坍缩
第二，坍缩后对相关边的权重做更新。

因此需要这样一个数据结构，它可以以 $O(1)$ 的复杂度选取最小权值，又可以最小消耗的动态更新相关边权重。——优先队列/最小堆

However，二次度量误差策略是一个典型的贪心算法。

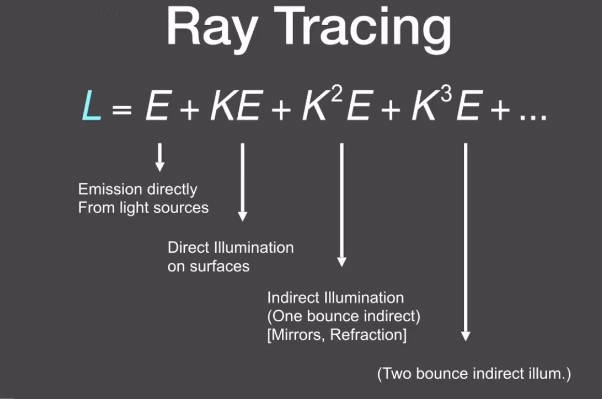
6 光线追踪 Ray Tracing

为什么要做光线追踪？因为光栅化不能很好的处理全局影响。光线是通过反射进入人眼成像的，冯氏反射模型只假设进行一次反射，但是实际上光线的反射非常复杂。比如有光泽的反射，间接光照（多次反射）。

However，光追是非常慢的。光栅化是实时的，光追是离线的。

6.1 光线假设

光线是直线传播的
光线与光线之间互不影响
光线必然是从光源出发最后进入人眼

6.2 循环光追 Recursive (Whitted-Style) Ray Tracing

6.2整节都是Whitted风格的光线追踪

Whitted-Style Ray Tracing是最早的光线追踪算法之一，由Turner Whitted于1980年提出。
这种方法通过递归地跟踪光线来模拟光线的行为。当一条光线与物体相交时，它会根据物体的表面特性进行反射、折射或吸收等操作，并在遇到光源或达到最大递归深度时结束追踪。
Whitted-Style Ray Tracing通常使用光线的反射、折射和环境光照等技术来模拟光线的行为，但不考虑光线在场景中的实际传播路径，因此在处理一些全局光照效果时可能存在局限性。

模拟光线反射的关系

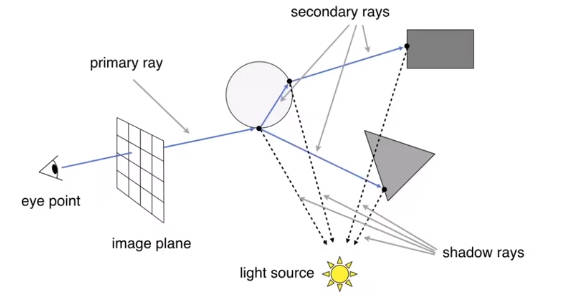
6.2.1 光线与平面的交点

6.2.1.1 光线公式

光线可以被视为从点光源发出的一个向量。具体可看下图：式中o是光源坐标，d是光线方向的单位向量，r(t)表示光线上任意一点

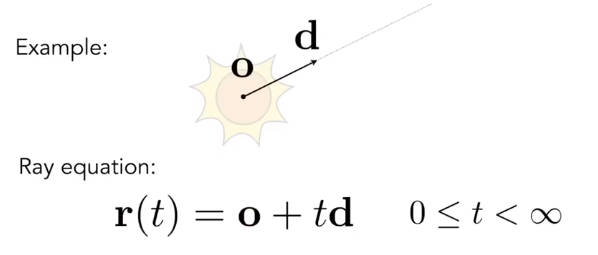
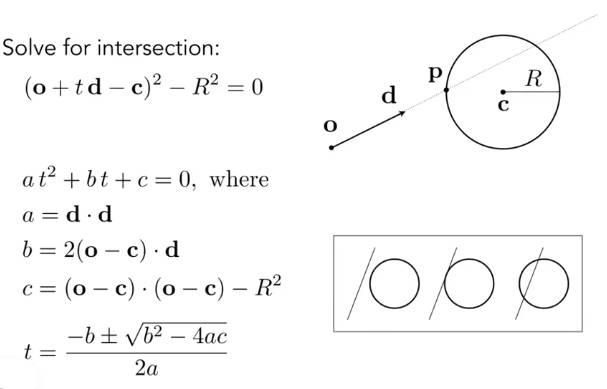
6.2.1.2 光线与球的交点

球面的定义： $p:(p-c)^2 - R^2 = 0$

$p$ 是球面的任意一点， $p$ 到球心 $c$ 的距离永远等半径

怎么定义交点？一个点即在光线上，又在球面上。所以联立公式并求解t：

6.2.1.3 光线与隐式表面的交点

隐式表面的定义： $p:f(p)=0$

交点公式： $f(o+td) = 0$

6.2.1.4 光线与三角形的交点

这个问题可以分解为两个问题：

光线与平面的交点
光线与平面的交点是否在三角形内

6.2.1.4.1 光线与平面的交点

点法式定义平面： $p:(p-p')\cdot N = 0$

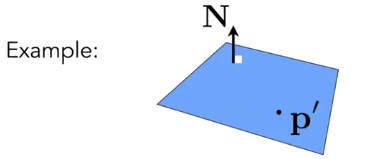
交点公式：

6.2.1.4.2 光线与平面的交点是否在三角形内

用重心坐标判断。用重心坐标来表示光线上的点。重心坐标相加等于1则在三角形内

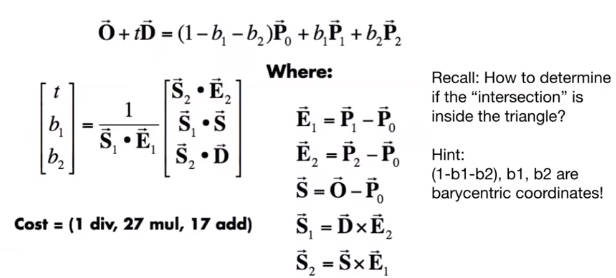
6.2.2 加速结构

6.2.2.1 包围盒 Bounding Volumes

当场景非常复杂时，三角形的数量是非常庞大的。

剪枝思想。一个朴素的观念：如果一束光连物体的包围盒都没有碰到，那么就没必要判断这束光与面的交点了。

包围盒一般由三个对面相交形成的。所谓对面就是平行的两个平面。

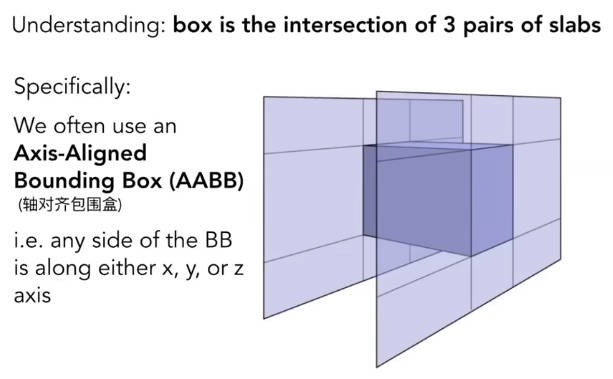
怎么判断光线是否进入以及什么时候进入了包围盒？

分别计算光线穿过一对面的时间 $t_{min}\&t_{max}$
在三个对面中选取最大的 $t_{min}$ 和最小的 $t_{max}$ 作为光线实际穿过这个包围盒的时间点
即 $t_{enter}=max\{t_{min}\},t_{exit}=min\{t_{max}\}$ ，若 $t_{enter}<t_{exit}$ 则说明光线实际穿过这个盒子

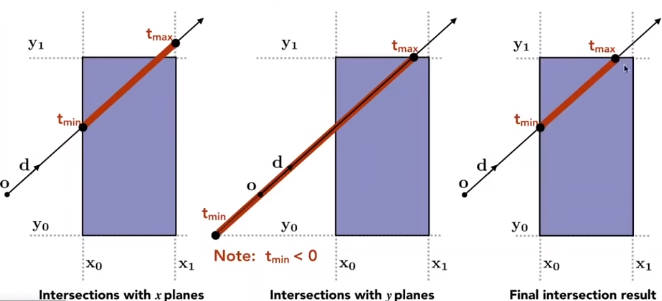
However，上述计算过程是将光线当作直线来计算的，所以t可能存在负值。

$\text{if } t_{exit}<0$ ，包围盒在光源背后，所以没有交点
$\text{if } t_{exit}>=0 and t_{enter}<0$ ，光源在盒子内部，有交点

总结

光线与包围盒有交点，当且仅当：

t_{enter}<t_{exit}\&\&t_{exit}>=0

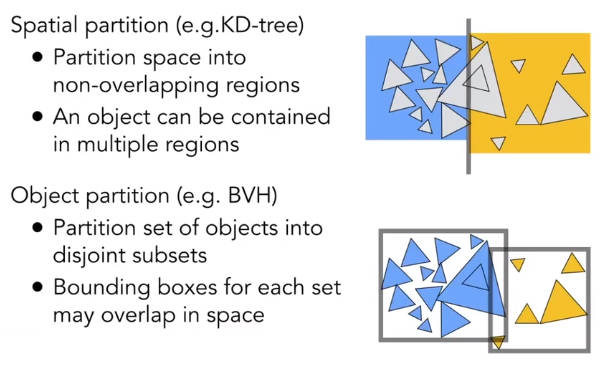
6.2.2.2 空间划分

通过包围盒判断了光线穿过盒子之后应该怎么做呢？

探寻光线在盒子内部与物体的相交情况。

光线只是一条线，对于一个盒子来说有大量的空间是这个光线不会涉及到的。所以要对盒子内部空间进行划分，只讨论光线附近的区域。

一个粗略的观念：判断光线是否穿过一个区域，远比直接计算光线与物体的交点要快。

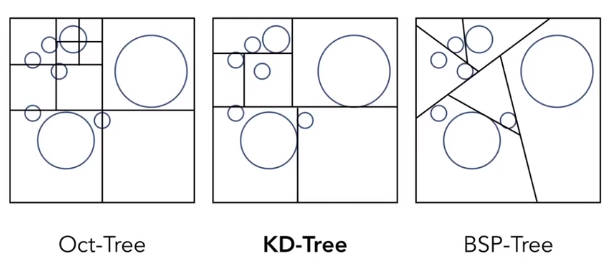
6.2.2.2.1 KD-Tree

KD树会将区域进行划分，划分之后的区域，都会和树的叶子节点对应。将光线与叶子节点所在区域进行是否穿过的判定。没有穿过的区域则可以不用考虑和物体的交点。只在穿过的区域中计算光线与物体的交点。

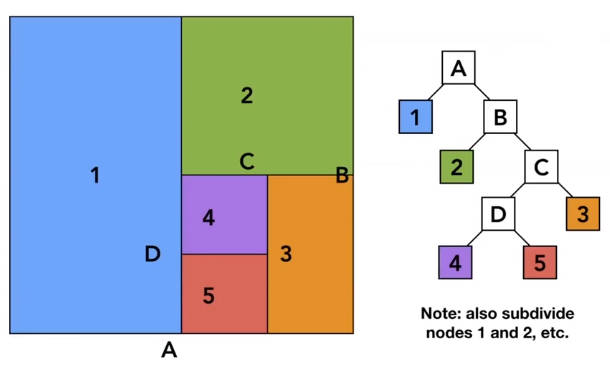
但是KD树有两个问题：

KD树的生成比较麻烦，也就是划分依据比较麻烦，需要考虑物体与划分区域的相交情况
一个物体可能存在多个划分区域内

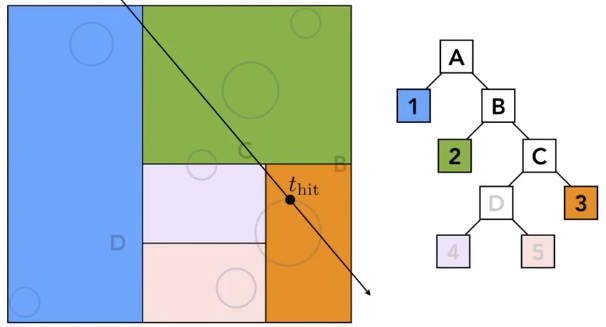
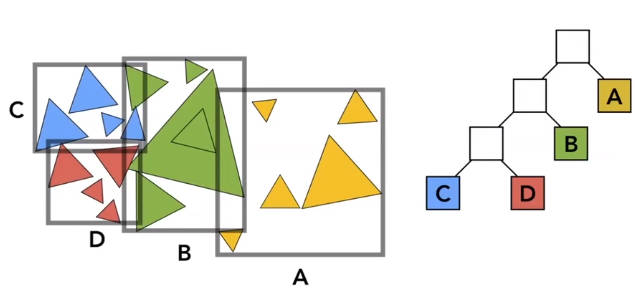
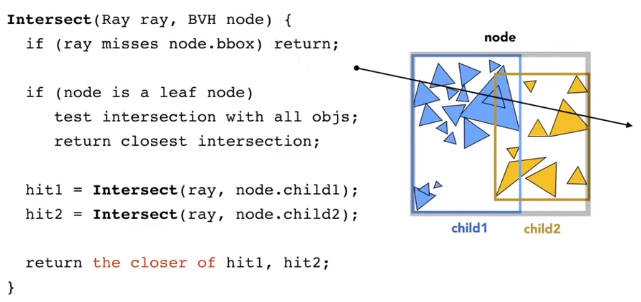
6.2.2.2.2 包围盒等级制度 Bounding Volume Hierarchy (BVH)

从包围盒的角度划分区域。

确定一个包围盒
将包围盒划分成两个包围盒（包围盒之间可以重叠，但是包围盒内部的物体不能重复，也就是说物体不是在这个盒子就是在那个盒子）
递归操作

如何衡量划分的好坏呢？一个朴素的观念是：包围盒的重叠区域尽可能地小

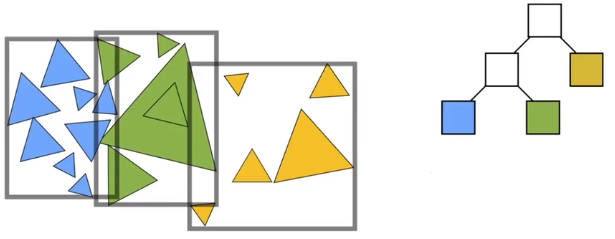
如何划分包围盒？

选择一个轴方向进行划分
技巧1：总是选择包围盒最长的轴方向进行划分
技巧2：找物体的第中位数个物体位置进行划分

KD树和BVH划分的区别

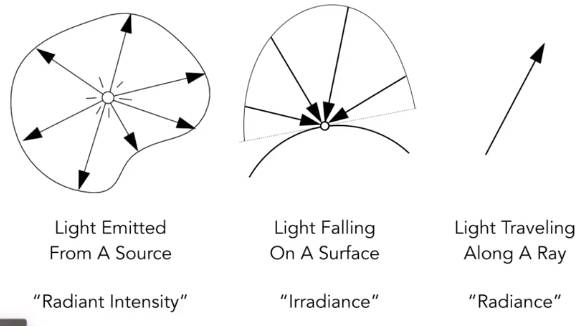
6.3 辐射度量学 Basic radiometry

辐射度量学描述的是光照系统。它假设光符合几何学，也就是上面Whitted的假设。

此外它提出了几个新概念：

Radiant flux：辐射通量
intensity：强度
irradiance：照度
Radiance：亮度

6.3.1 辐射能和通量(功率) Radiant Energy and Flux(Power)

定义：Radiant Energy 是光源辐射出来的能量

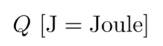
定义：Flux(Power) 是单位时间的辐射能。 $W$ 是瓦特，能量的单位。 $lm$ 是流明，表示光源的亮度。

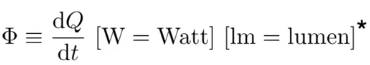
6.3.2 辐射强度 Radiant intensity

定义：辐射强度是指光源在单位时间单位立体角上辐射出的能量

定义：立体角是球一个局部表面积除以半径的平方

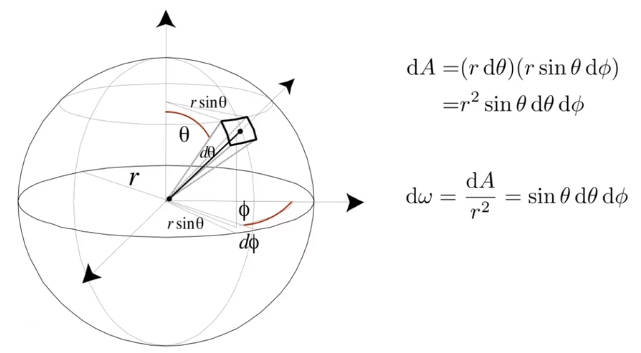
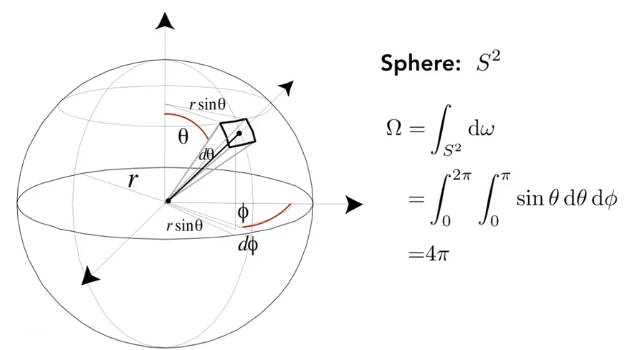
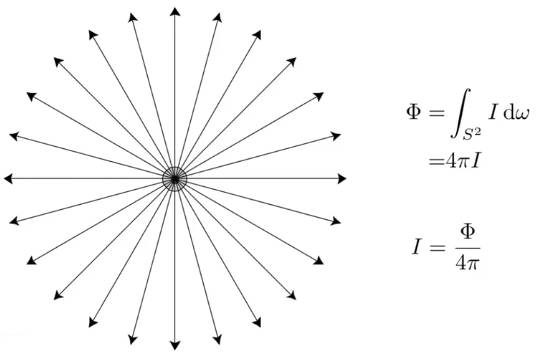
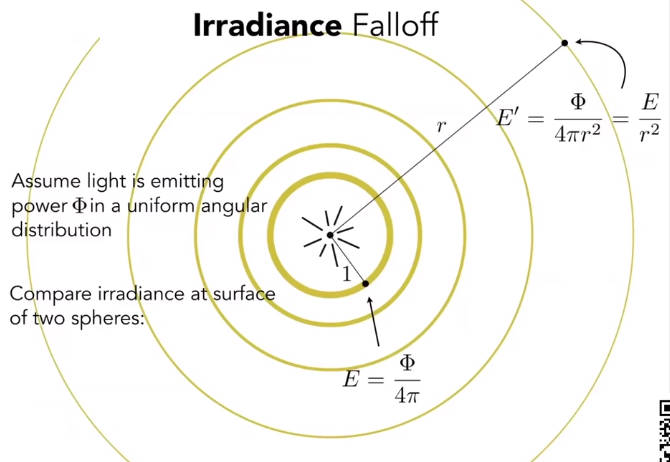
6.3.3 照度 irradiance

定义：irradiance 是入射到一个表面点上的单位面积的功率.

哪个单位面积？光源传播出来的球壳的单位面积，传播出的能量随半径的平方衰减。

照度会随着传播距离衰减，但是强度不会。

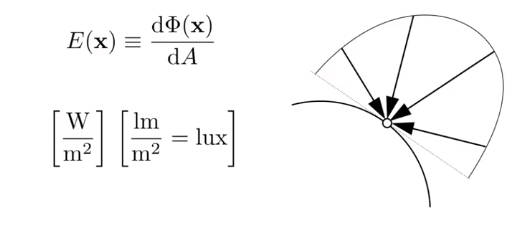
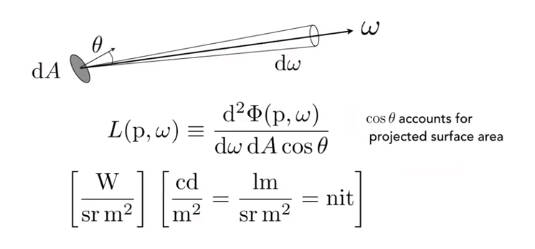
6.3.4 亮度 Radiance

定义：Radiance是功率在单位立体角和单位投影面积上的能量是多少

也可以理解为每单位立体角有多少照度，或者每单位面积有多少强度

再换句话说，irradiance就是将来自四面八方的radiance积分

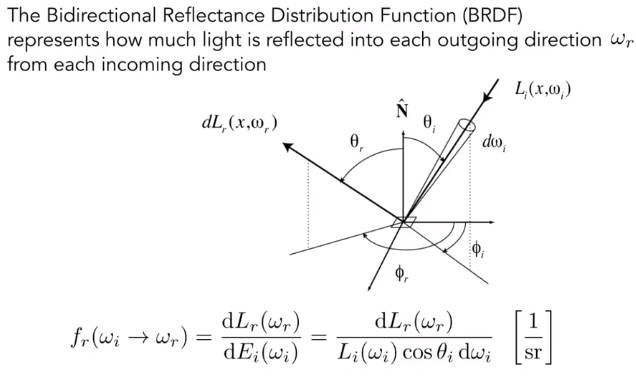
6.3.5 双向反射分布函数 Bidirectional Reflectance Distribution Function (BRDF)

已知入射光能量和角度，射到物体表面会向各个方向辐射，辐射出去的能量跟角度是不一样的。

也可以理解为物体表面一点，通过亮度吸收了多少能量。再以这一点作为光源辐射除去。

BRDF函数用来描述这样一个概念：微小面积dA从某一个微小立体角dw接收到的照度（irradiance）后，会如何被分配到各个不同的立体角上去(比例，能量根据立体角在空间中的分布）。

再类比一下，BRDF和冯氏反射模型中的漫反射系数 $k_d$ 有异曲同工之妙

但是！！物体接收的光可不止是来自光源的。光线的反射不止一次，物体会接受来自其他物体的光。这种情况开始变得复杂，需要递归来进行计算。后文接着说。

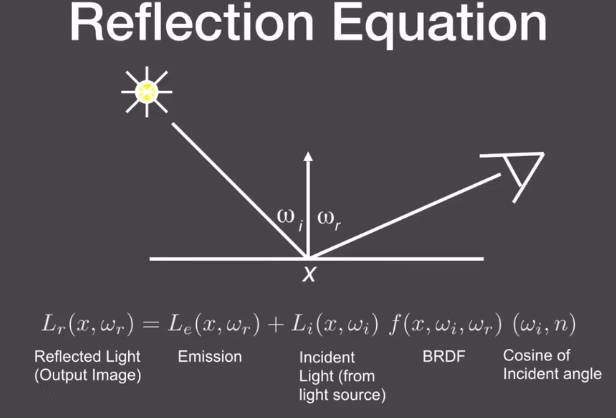
6.3.6 渲染方程

如果物体本身也会发光呢？用 $L_e(p,\omega_o)$ 来表示自发光的照度。 $\Omega^+和H^2$ 都表示半球。 $n\cdot\omega_i$ 表示所有光都是指向外部的。

为什么是半球？因为这里假设光不会从物体表面下打出来。

限制在物体表面的光线传播都是满足这个渲染方程的。

这是当时提出渲染方程时，作者贴出的图。

6.3.7 如何理解渲染方程

当只有一个点光源时，图像接受的光等于自发光和反射的光

当有多个点光源时，就将多个点光源反射的照度相加就行了。

当有面光源时，其实就是无数个连续的点光源。所以求和变成了对单位立体角的积分。

将其他物体反射的光作为光源，就相当于多了许多面光源。

因为这里的入射角度为了方便函数计算都是规定为从反射点朝外的，但是这里的入射角作为另一个点的出射角是从外射向当前点的，所以正好相反，这里加一个负号就可以直接递归了

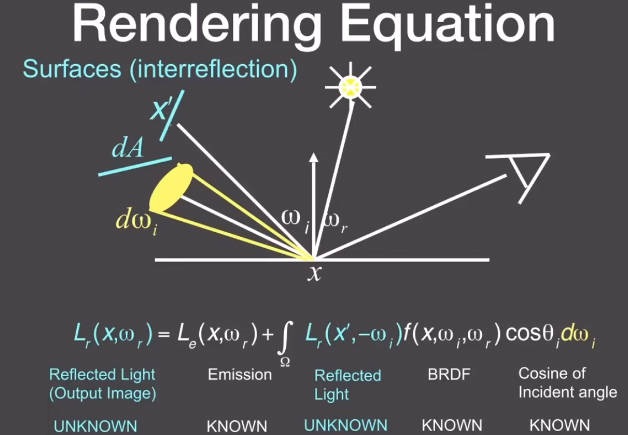
通过数学方式的简写，公式变为：

再简写：？？？？？泛函？

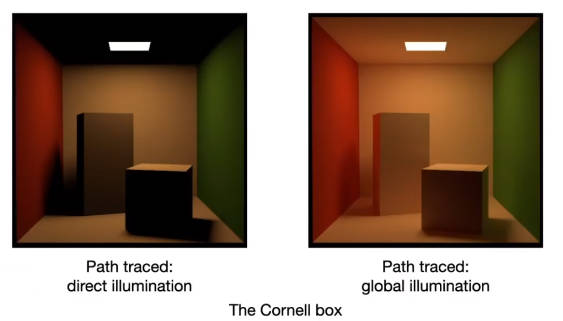
6.3.8 一个全局光照渲染的例子

全局光照就是直接光源加上反射光源。

这是只有直接光照的图像。

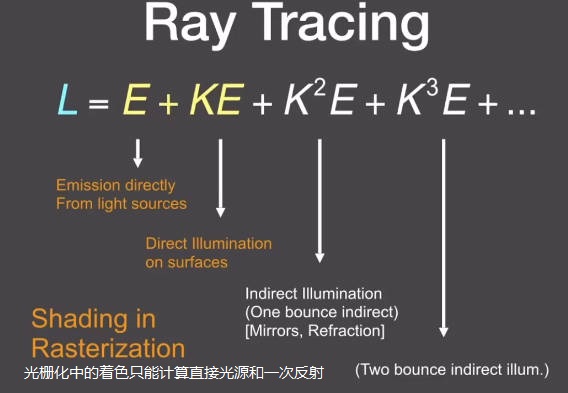
光线弹射一次，光栅化只能渲染到这个程度。

光线弹射两次

光线弹射16次

6.4 蒙特卡洛积分 Monte Carlo Integration

概率论回顾

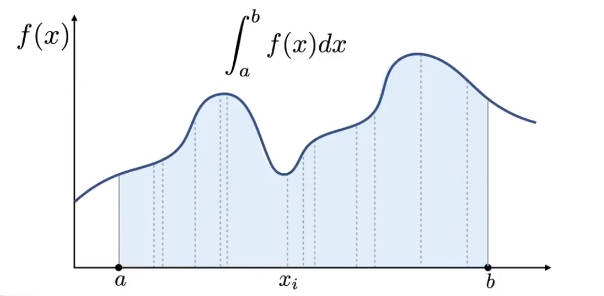
为什么用蒙特卡洛积分？积分函数太过复杂，以至于无法求出积分后的函数。好在定积分最后的结果是数值，所以可以直接得到数值解而非解析解。

怎么得到数值解？

首先需要理解蒙特克罗积分是怎么计算的。

如下图。多次进行随机采样，采样就是取一个值 $x_i$ ，然后计算一个矩形的面积 $f(x_i)*(b-a)$ 。一次采样的面积肯定不准，于是进行多次随机采样，然后取平均。最后的平均值会近似为实际的定积分数值解。

将上述思想形式化：这里的 $p(x)$ 是均匀分布的概率密度函数

进一步通用的表示：积分的对象和采样的对象是同一个

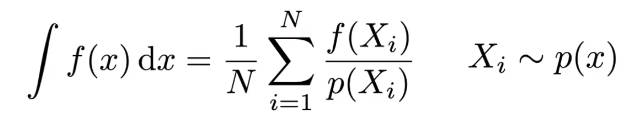
6.5 路径追踪 path tracing

路径追踪就是求解渲染方程。追踪的路径就是指定方位角的光线。

使用蒙特卡洛积分求解渲染方程中的定积分：

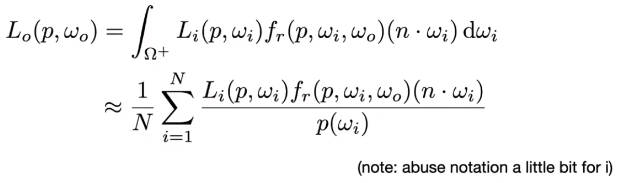
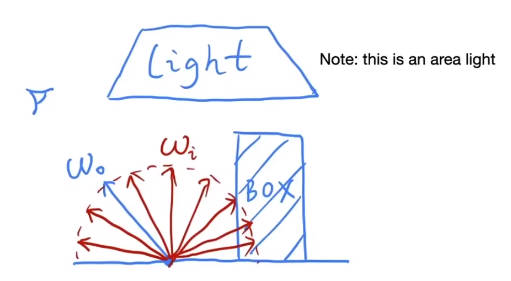
注意理解 $\omega_o和\omega_i$ 的方向： $\omega_o$ 是指向人眼的观测光线， $\omega_i$ 是四周反射过来的光线，但是方向是指向反射源或者光源

所有向量全是朝外的。

渲染方程求解的伪代码：

Trace a ray就是计算指点方位角后的光线表达。
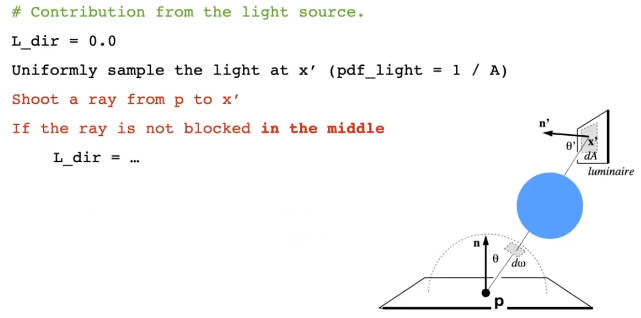
$\omega_i$ 是从着色点出发，指向光源
pdf是指概率密度函数

上述只是求解直接光源的伪代码。现在考虑由物体反射出来的间接光源：

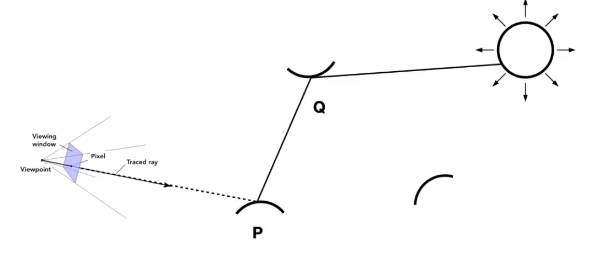
shade(q,-wi)是指 $\omega_i$ 由着色点指向了另一个物体，那么从另一个物体指回来的就是 $-\omega_i$ 了

但是！！！

现在有两个问题：

光线数量会爆炸。因为渲染方程认为一个光线打过来，反射后会有无数根光线打出去，多次反射，光线数量会成指数级爆炸。
没有递归停止条件

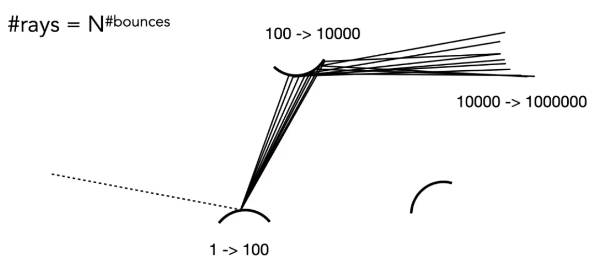
6.5.1 光线爆炸

如何避免爆炸？需要思考这样一个问题，反射后的光线数量是几才不会发生爆炸？——1个

所以修改一下伪代码，现在只计算（随机采样）一根光线：

现在的光线追踪通常假设反射的光线只有一条。大于一条的方法称为分布式路径追踪。

但是只采样一条路径，蒙特卡洛的结果就会不准确。

这没有问题，因为一个像素会接受多个光线，只要追踪更多的光线再平均就好了。也就是说不是在反射出多次采样，而是在像素位置多次采样。相当于在像素处进行蒙特卡洛积分

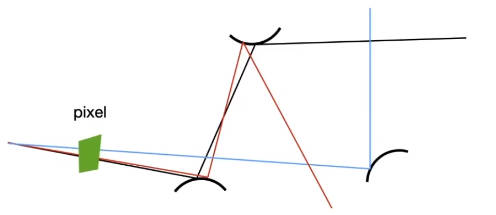
伪代码写为：

在像素内均匀采样N个位置
根据相机位姿，从相机的光心打出一条光线穿过采样点
如果光线打到了场景中的某一点，就计算这一点的着色

6.5.2 无限递归

以上解决了光线爆炸问题，接下来考虑递归的结束问题。

真实世界的光线是弹射无数次的，相当于递归也是无数次的。如果中途停止，这意味着砍掉了部分光的能量。

为了解决这个两难境界，使用了俄罗斯轮盘赌。

首先，我们预期某一个着色点的出射亮度是 $L_o$ ，现在想停止光线追踪，但是又不想损失光线能量，想要光线追踪的结果仍然是 $L_o$ 。
认为的设定轮盘赌的概率P，也就是按概率P继续追踪，返回 $L_o/P$
以概率1-P返回0（dropout？）
最后的期望仍然是 $L_o$ ： $E=P*(L_o/P)+(1-P)*0=L_o$ （无偏估计？）

但是 $L_o$ 不是预先知道的啊？

没关系， $L_o$ 暗含在程序的递归表达式里。

所以伪代码修改为：

人为设定一个概率
随机生成一个数来判断是否停止
其他相同，只是在递归返回值处除以指定概率

6.5.3 采样光线

解决掉上述两个问题后，仍然有一个小问题。采样光线的浪费，如下图。如果面光源大，那么可能只要5个光线就会有一个打到光源。如果面光源小，可能要有50000个光线才会有一个打到光源。这就会造成大量的光线浪费。

为了避免浪费，一种朴素的想法：既然从像素出发进行采样，会有大量光线打不到光源，那么就从光源出发进行采样，这样就不会有光线浪费。

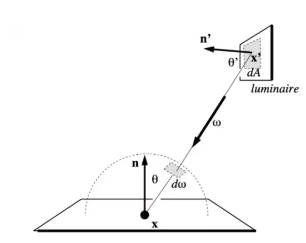
在光源上采样怎么采？因为光源后面没有类似相机成像点的东西，所以不能像像素采样那样改变光线方向。

假设在光源上均匀采样，那么就是按单位面积采样。

可以写作 $\text{pdf}(概率密度函数)=1/A$ ，因为 $\int \text{pdf}* \text{d}A=1$ 。

但是渲染方程的积分对象是方位角 $\omega$ ， $L_o=\int L_i*fr*cos*\text{d}\omega$ 。

蒙特卡洛积分规定必须对积分对象进行采样。因此为了采样方位角，我们需要知道方位角 $\text{d}\omega$ 和 $\text{d}A$ 的关系。

回顾方位角的定义： $\text{d}\omega = \frac{\text{d}A}{R^2}$ ，单位球表面积除以半径的平方。

因此，以着色点 $x$ 为球心，以光源采样点 $x'$ 和着色点 $x$ 的连线为半径，做球。将光源采样点的单位表面积 $\text{d}A$ 投影到球面上，就可以将采样面积和方位角联系起来。因为是单位面积，所以不用考虑平面投影和球面投影的区别。

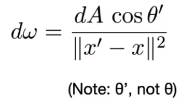
于是重写渲染方程：

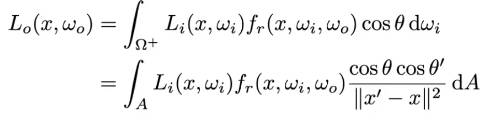
重写之后就要对伪代码进行再次修改：

将程序分为两种情况，第一种情况是直接光照（只有一次反射），就用现在重写后的渲染方程；第二种情况是间接光照，则使用从像素采样的方法不变

到此只有最后一个小问题：判断着色点和光源之间是否有遮挡：

6.6 总结

以往的光追指的是Whitted-style的理论。

现在的光追包括：路径追踪、Photon mapping、Metropolis light transport、VCM、UPBP

辐射亮度到颜色的转变需要通过gamma校正

BRDF涉及到镜面反射会有一个delta函数计算

7 材质的外观

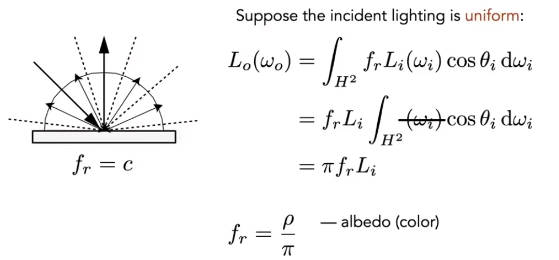
材质=BRDF

$\rho$ 是反射率，可以是三通道或者其他的。 $L_i$ 是着色点接受到的总能量，假设能量守恒，物体不吸收能量。

8 相机、镜头和光场

应用知识

如何判别一个场景是否渲染的好
- 其中一个标准是看场景亮不亮，这反映了渲染时的全局光照质量。亮的时候，细节的粗糙就会显露出来
如何判断一个点是否在物体内部？
- 平面可用向量叉乘
- 三角形面可用重心坐标
- 更通用的方法：以该点为光源，任意打出一条射线。射线与物体的交点是奇数，则点在内部，偶数次则在外部。（相切不算相交，同理在表面也不算是在内部）

GAMES101_现代计算机图形学基础

GAMES101_现代计算机图形学基础

1 线性代数基础知识

1.1 向量乘法

1.1.1 向量点乘

1.1.2 向量叉乘

1.2 正交坐标公式

1.3 矩阵

1.3.1 向量的点积和叉乘写成矩阵形式

2 变换 Transformation

2.1 线性变换

2.1.1 缩放变换 Scale Transform

2.1.2 反射变换 Reflection transformation

2.1.3 切向变换 Shear Matrix

2.1.4 旋转变换 Rotation Transform

2.1.5 线性变换

2.2 仿射变换

2.2.1 平移变换和齐次坐标

2.2.2 逆变换 Inverse Transform

2.2.3 变换的组合

2.2.4 三维变换

2.2.4.1 绕坐标轴旋转

2.2.4.2 绕任意轴旋转

2.3 观测变换 Viewing transformation

2.3.1 视图变换 View/Camera transformation

2.3.2 投影变换 Projection transformation

2.3.2.1 正交投影

2.3.2.2 透视投影

2.3.3 投影到成像平面

2.3.4 如何理解MVP model view projection

3 三角形光栅化 Rasterization

3.1 三角形 - 基本形状单元 foundamental shape primitives

3.2 如何在屏幕中画一个三角形

3.2.1 三角形的包围盒 Bounding Box

3.3 反走样 抗锯齿 anti-aliasing

3.3.1 采样问题 Sampling Artifacts

3.3.1.1 锯齿 Jaggies

3.3.1.2 摩尔纹

3.3.1.3 车轮错觉

3.3.2 反走样的方法

3.3.2.1 如何理解图像的高频信息

3.3.2.2 空域与频域的卷积

3.3.2.3 如何理解采样

3.3.2.4 实际反走样的操作

3.3.2.4.1 SSAA（超采样反走样）

3.3.2.4.2 MSAA(多重采样反走样 Multisample anti aliasing)

3.4 总结

4 着色 Shading

4.1 画家算法

4.2 深度缓存 Z-buffer

4.3 一个简单的着色模型-冯氏反射模型 (Blinn-Phong Reflectance Model)

4.3.1 漫反射 Diffuse Term

4.3.1.1 光的接收

4.3.1.2 光的传播

4.3.1.3 漫反射公式

4.3.2 高光 Specular Term

4.3.3 环境光 Ambient Term

4.3.4 完整的冯氏反射模型

4.4 着色频率

4.4.1 平面着色 Flat shading

4.4.2 顶点着色（高洛德着色）Gouraud shading

4.4.3 像素着色 Phong shading

4.4.4 着色频率的两个问题

4.4.4.1 怎么知道逐顶点着色的顶点法线是什么

4.4.4.2 怎么知道逐像素着色的像素法线是什么

4.5 图像管线\实时渲染管线 Graphics Pipeline

4.6 纹理映射 Texture map

4.6.1 纹理映射存在的问题

4.6.1.1 纹理放大

4.6.1.2 纹理太大或者说纹理太细

4.6.1.2.1 三线性插值 Mipmap

4.6.1.2.2 各向异性过滤 Ripmap

4.6.1.2.3 其他方法 （？）

4.6.2 纹理映射的应用

4.6.2.1 环境映射

4.6.2.2 凹凸贴图/法线贴图

4.6.2.3 位移贴图

4.6.2.4 3D泊松噪声 + 立体模型

4.6.2.5 存储已经计算好的着色信息

4.6.2.6 体渲染

3.3 反走样抗锯齿 anti-aliasing

4.6.1.2.3 其他方法（？）