MRME：基于最小相对运动熵的图像配准特征匹配

MRME：基于最小相对运动熵的图像配准特征匹配(2021)

摘要

精确的点匹配被广泛使用，是基于特征的图像配准中一个关键且具有挑战性的过程。为了提高具有重异常值和相似局部结构的假定匹配的特征匹配精度，提出了一种基于最小相对运动熵（MRME）的精确且鲁棒的特征点匹配算法，其中假定匹配与其K最近点之间的相对运动邻居是制定的。基于相对运动聚类结果，定义相对运动熵来寻找重合的相对运动。根据与 MRME 的相对运动，在两阶段特征匹配策略中去除异常值。通过准线性时间复杂度，具有随机或不规则相对运动的异常值被有效且准确地去除，而具有重合相对运动的异常值被保留。三个具有重复模式、视点变化、低重叠区域和局部变形的数据集用于展示所提出算法的性能。 MRME 被证明比十种最先进的特征匹配算法更健壮和准确。

关键词：基于密度的噪声应用空间聚类 (DBSCAN)、局部结构相似性、失配消除、点匹配、相对运动熵 (RME)、空间聚类。

1. 引言

图像配准用于许多遥感应用，例如图像拼接、图像融合、环境监测和变化检测 [1]-[4]。它是在几何上对齐从不同视点、不同时间或由不同传感器拍摄的同一场景的两个或多个图像的过程。大多数图像配准方法是基于区域或基于特征的。基于强度分布的相似性，基于区域的方法通常耗时且对噪声敏感，而基于局部结构和几何约束的光照变化、图像失真和基于特征的方法更有效和鲁棒。尽管有些方法既基于特征又基于区域[5]-[7]，但基于特征的方法仍然是遥感图像处理中研究和使用最广泛的方法。特征点匹配是基于特征的图像配准中一个典型的关键问题。通常，为了匹配特征点，根据局部特征描述符的相似性建立假定的对应关系，并去除异常值以获得精确匹配结果。在本文中，我们关注的是遥感图像配准的特征点匹配问题。

尽管已经提出了许多新的特征描述符[8]-[12]，但仍然存在一些问题使得基于特征的遥感图像配准变得困难。首先，在不同时间拍摄，视点和光线条件可能不同。因此，物体的外观也可能发生变化，其特征可能并不完全相同。其次，异常值将不可避免地与重复对象的存在保持一致，例如建筑物、农田和道路。第三，当重叠区域较低时，非重叠区域可能存在许多不匹配。第四，受海流和波浪的影响，海面的冰和绿潮图像的局部变形使得变换参数难以估计。

已经进行了大量研究以进一步细化特征匹配结果。在一个点周围的小区域中具有物理约束，特征点之间的局部邻域结构将更有可能被保留。基于这种直觉，Ma 等人。 [13]提出了一种有效的特征匹配方法，局部保持匹配（LPM），它使用假定匹配与其邻居之间的绝对运动来评估邻域拓扑的一致性。受绝对运动共识的约束，有效地消除了具有不同邻域的不匹配。凭借绝对运动一致性，提出了一种基于学习的失配消除算法、失配消除学习 (LMR) [14] 和基于空间聚类的鲁棒特征匹配 RFM-SCAN [15]。这些方法有效且稳健，可以保留与绝对运动一致的假定匹配。然而，对于大量异常值和相似的局部结构，它们很难消除具有伪同构结构的所有异常值。

在本文中，利用假定匹配之间的相对运动来提高特征匹配的准确性。提出了一种基于最小相对运动熵（MRME）的判别特征点匹配方法来准确滤除不匹配。特征匹配问题被认为是一个局部相对运动一致性估计问题，为此制定了相对线性运动和相对角运动。定义相对运动熵 (RME) 是为了区分内点 (RMBI) 与离群点 (RMWO) 之间的相对运动。与 MRME 的对应关系被保留为正确的匹配项。

本文的贡献如下。

1. 假定匹配之间的局部相对运动被定义为相对线性运动和相对角运动，以评估相对运动一致性。
2. 为了找到重合的相对运动，提出了RME。
3. 基于具有MRME的集群，定义了新的成本函数，并设计了两阶段的异常值去除策略。

本文的其余部分组织如下。第二部分简要回顾了相关工作。第三节介绍了基于最小相对运动一致性熵的特征匹配方法。第四节给出了实验结果和性能分析。结论在第五节中得出。

2. 相关工作

特征匹配算法可以分类为重采样、基于变换模型、图匹配和基于局部结构一致性。

随机样本一致性（RANSAC）[16]，这是一种基于重采样的方法，它从一组包含异常值的观察数据中迭代地估计数学模型的参数。从某种意义上说，它是非确定性的，它仅以一定的概率产生合理的结果。受 RANSAC 的启发，已经提出了许多类似 RANSAC 的方法 [17]。通过修改采样策略，MLESAC [18]、渐进式样本共识 (PROSAC) [19] 和图形切割 RANSAC (GC-RANSAC) [20] 增加了早期选择全内点样本的概率。 MLESAC 选择最大化可能性的解决方案，而不仅仅是内点的数量。在实践中，MLESAC 结果通常优于 RANSAC 的内部计数。 PROSAC 通过预测内部概率来利用点的排序。 GC-RANSAC 在局部优化步骤中运行图切割算法来分离内点和异常点。边缘化样本共识（MAGSAC）使用 σ - 共识在一系列噪声尺度上边缘化 σ，并通过加权最小二乘拟合获得优化模型。粒子群优化样本共识（PSOSAC）[21]直接对模态变换参数进行采样，而不是随机选择试探性匹配。基于三角形区域表示的仿射不变性，鲁棒样本一致性判断（RSCJ）[22]可以有效地识别不良样本，因此可以以令人满意的准确度显着降低计算量。这些算法可能不适用于大部分异常值。

最显着的基于几何变换的简单特征匹配算法，迭代最近点（ICP）[23]，迭代地找到最优匹配结果。它的主要缺点是需要良好的初始估计来保证正确的解决方案，因此在存在噪声的情况下它不能很好地工作。为了改进非刚性变换点匹配的 ICP，基于软分配、确定性退火和薄板样条，Chui 和 Rangarajan [24] 构建了一个通用框架薄板样条鲁棒点匹配 (TPS-RPM)。 Myronenko 和 Song [25] 引入了一种概率方法，即相干点漂移 (CPD)，在存在噪声、异常值和缺失点的情况下解决刚性和非刚性变换的点集配准问题。 Chui 和 Rangarajan [24] 开发了 TPS-RPM 来解决非刚性配准的点对应问题。 Ma 等人将局部几何约束引入到特征匹配的最大似然公式中。 [26] 提出了用于刚性、仿射和非刚性特征匹配的 LLT。通过利用具有归一化数据点和全局信息的多层感知器 (MLP)，Yi 等人。 [27] 提出了学习寻找良好对应关系 (LFGC) 以将对应关系标记为内点或异常点，同时恢复基本矩阵。假设基于几何模型的方法可以获得较高的精度，但在实践中，当异常值过多时，很难获得准确的变换模型，这会降低这些算法的鲁棒性。然而，迭代估计转换模型非常耗时，这使得它们的效率降低。

图匹配方法通常将特征匹配表述为二次分配问题（QAP）。此类方法包括光谱匹配 (SM) [28]、具有仿射约束的 SM (SMAC) [29]、图位移 [30] 和其他 [31]、[32]。然而，众所周知，QAP 是 NP 难的。使用分支定界变体的精确最优算法仅适用于非常小的图（例如，30 个节点）[33]。为了解决这些问题，Zhou 等人。 [34] 提出了分解图匹配（FGM），将大的成对关联矩阵分解为较小的矩阵，以评估局部结构一致性。 FGM 将 GM 方法与经典的 ICP 算法相结合，使其能够匹配受全局刚性和非刚性几何约束的图，但仍然不适合匹配大型特征集。

已经提出了许多基于局部结构一致性的方法来提高特征点匹配的准确性和鲁棒性。阿格利亚尔等人。 [35] 提出了图变换匹配 (GTM)，它过滤 K 近邻 (KNN) 平均距离并消除异常值以获得两个共识图。然而，平均距离可能因图像而异，存在不可避免地保留为内点的异常值。 Liu等人提出了基于相邻点空间顺序差异的受限空间顺序约束（restricted spatial order constraint，RSOC）。 [36]。 Izadi 和 Saeedi [37] 提出了 GTM 的改进版本，加权 GTM (WGTM)，它利用了假定匹配之间的几何（角距离）关系。基于 KNN 密度估计和空间顺序约束，Meng 等人。 [38]提出了空间顺序约束双边邻居投票（SOCBV），将有向KNN图和双边邻居投票引入后验内点概率估计以获得准确的匹配。在迭代检查局部结构相似性时，这些算法缺乏实际应用的效率。 Bian 等人将平滑度约束纳入分离的统计框架。 [39] 提出了用于快速特征匹配的基于网格的运动统计 (GMS)。 Ma等人进行了很多研究，提出了很多点匹配方法。 [13]、[14]、[26]，基于局部结构一致性。通过保留潜在真实匹配的局部邻域结构，设计了一种有效的方法 LPM。在邻域拓扑的共识下，提出了一种基于学习的方法、学习不匹配消除 (LMR) [14]、基于空间聚类的方法以及使用空间聚类 (RFM-SCAN) 的鲁棒特征匹配。通过检查每个假定匹配与相应单元中的典型运动向量之间的一致性，线性自适应过滤 (LAF) [40] 使用几何一致性先验以及过滤和去噪理论来去除异常值。没有变换模型估计，这些算法更有效。由于相似特征的存在，这些方法很难去除被伪同构结构包围的异常值。提出了一种异常值去除方法，局部结构一致性约束（LSCC）[41]，该方法使用新的局部结构描述符评估每个对应关系以消除错误匹配。然而，当异常值过多时，LSCC 中的局部结构描述符可能不够健壮，无法去除所有异常值。

3. 方法

我们介绍了我们的判别特征匹配方法来匹配两个具有重异常值和相似局部结构的特征点集。通过首先比较最近邻居与 SIFT 描述符的第二近邻居的距离来建立推定的匹配。特征匹配被认为是一个相对运动一致性问题。问题制定和匹配策略如下。

3.1 局部相对运动

为了评估局部相对运动的一致性，将假定匹配与其邻域之间的局部相对运动分解为相对线性运动和相对角运动。

给定从遥感图像对中检测到的两个假定对应点集$P=p_1,p_2,...,p_i,...,p_n$和$Q=q_1,q_2,...,q_i,...,q_n$假定对应点$p_i$和$q_i$及其对应的邻居$p_j$和$q_j$之间的相对运动向量$v_{ij}$和$u_{ij}$被定义，如图 1 所示。

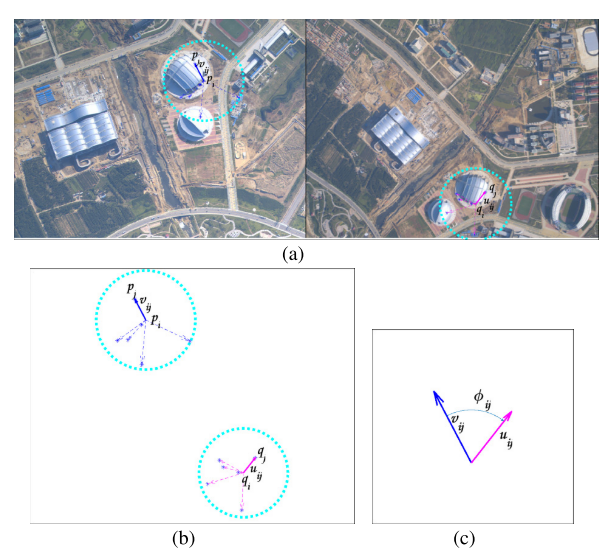
图1. 相对速度示意图。 (a) 和 (b) 假定对应点之间的相对运动矢量$v_{ij}$和$u_{ij}$。 © 矢量$v_{ij}$和$u_{ij}$之间的角速度。

开始时，基于相对运动矢量$v_{ij}$和$u_{ij}$，对应点$p_i$和$q_i$之间的相对线速度$\eta_{ij}$定义为：

$\eta_{ij}=\frac{|v_{ij}|}{|u_{ij}|}\tag{1}$

基于相对线速度$\eta_{ij}$，相对直线运动$s_{ij}$定义为：

$\begin{aligned} s_{ij}&=\log(\eta_{ij})\\ &=\log\Big(\frac{|v_{ij}|}{|u_{ij}|}\Big)\\ &=\log(|v_{ij}|)-\log(|u_{ij}|) \end{aligned}\tag{2}$

$v_{ij}$和$u_{ij}$的倾角分别定义为

$\theta(v_{ij})=atan2( (p_j.y-p_i.y),(p_j.x-p_i.x) ) \\ \theta(u_{ij})=atan2( (q_j.y-q_i.y),(q_j.x-q_i.x) ) \tag{3}$

其中 atan2(·) 是四象限反正切，它返回闭区间 [−π, π] 中的值。

则向量$v_{ij}$和$u_{ij}$之间的角速度为

$\phi_{ij}=\theta(v_{ij})-\theta(u_{ij})\tag{4}$

通过将$\phi_{ij}$限制为 [−π, π]，相对角运动$r_{ij}$定义为：

$r_{ij}= \begin{cases} \phi_{ij}-2\pi,&\phi_{ij}>\pi\\ \phi_{ij},&-\pi<\phi_{ij}<\pi\\ \phi_{ij}+2\pi,&\phi_{ij}<-\pi \end{cases}\tag{5}$

其中$r_{ij}$被限制为 [−π, π]，这使得区分变得容易。

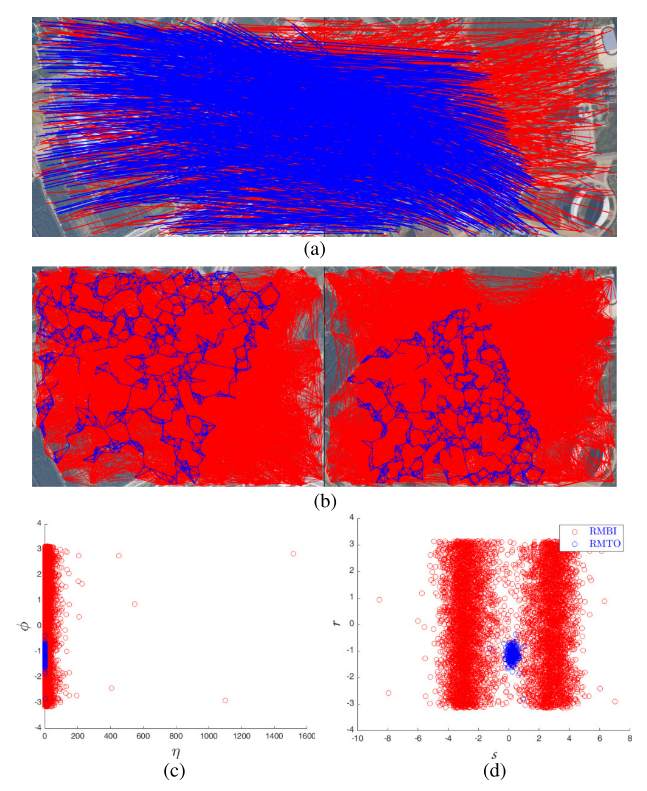
图 2 显示了图 1 中假定匹配的相对速度和相对运动。图 2(a) 展示了两个图像中假定的点对应关系。相应的 KNN 图在图 2（b）中给出。红色点和线表示异常值和带有异常值的边，蓝色点和线表示内点和内点之间的边。对应关系及其公共最近邻之间的相对线速度$\eta_{ij}$和相对角速度$\phi_{ij}$分别用公式（1）和（4）计算。

在图 2（c）中，红点是具有异常值的相对速度（RVWO），蓝点是异常值之间的相对速度（RVBI）。由于大多数 η 集中在零附近，因此很难通过相对速度的分布来区分异常值和异常值。

为了使内部点与异常点区分开来，相对角运动$S=\{s_{ij}|p_j\in N_{p_i}\ or\ q_j\in N_{q_i}\}$和相对直线运动$R=\{r_{ij}|p_j\in N_{p_i}\ or\ q_j\in N_{q_i}\}$分别用公式 (2) 和 (5) 计算，其中$N_{p_i}$和$N_{q_i}$分别是$p_i$和$q_i$的邻居。

如图2（d）所示，蓝色的RMBI和红色的RMWO以不同的密度分布。离群点的相对运动高度集中在一个小区域内，而离群点之间的相对运动是均匀分布的。基于相对直线运动和相对角运动，设计了一种相对运动一致性求解策略，以找到具有重合相对运动的内点。

3.2 最小相对运动熵

如图 2（d）所示，RMBI 集中在高密度的小区域，这与 RMWO 不同。因此，我们可以根据相对运动的分布来检测RMBI。为了在数据空间中找到由点密度较低的区域分隔的密集区域，Ester 等人[42] 提出了基于密度的噪声应用空间聚类（DBSCAN）。它将至少一个最小数量 (minpts) 的点组合在一起，这些点是 epsilon 邻域作为一个集群，而将单独位于低密度区域（其最近的邻居距离太远）的点作为异常值。为了找到具有重合相对运动的最可能对应的向量 v 和 u，将相对运动一致性解问题转换为空间聚类问题。 DBSCAN 被用来发现密集区域作为 s 和 r 空间中的 RMBI 簇。

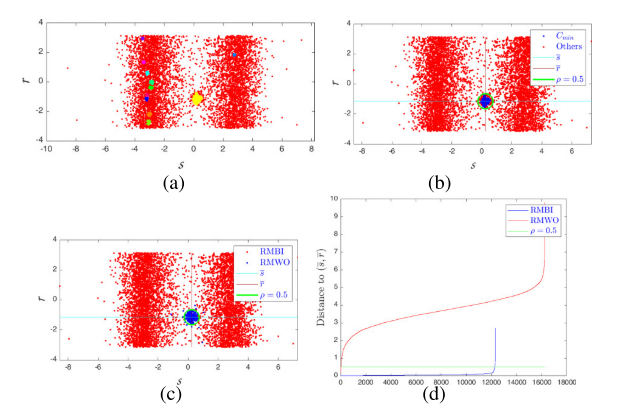
然而，当异常值过多时，图 3（a）的聚类结果中可能存在多个候选聚类，其中聚类以不同的颜色标记。哪个集群由 RMBIs 组成？

RMBI 簇中的相对运动通常在重复的内点之间，而 RMWO 簇中的相对运动更可能在不同的异常点之间。这意味着与 RMBI 簇相关的推定匹配的无序度应低于与 RMWO 簇相关的匹配度。为了区分RMBI的集群和RMWO的集群，每个相对运动集群的RME是基于与相对运动集群相关的推定匹配来定义的。

给定候选相对运动簇$C=\{C_1,C_2,...,C_M\}$，假定的匹配列表 Ik 与集群 Ck 中的相对运动相关，被定义为将 RME 评估为

$I_k=\{i,j|c_{ij}=(s_{ij},r_{ij})\in C_k\}\tag{6}$

以$I_k$作为具有独立样本的平稳信号，簇$C_k$的 RME 估计为

$RME(C_k)=entropy(I_k)\tag{7}$

为了计算$I_k$的熵，估计一个直方图，熵由 Moddemeijer [43] 的基于直方图的方法确定。

内点更可能有共同的内点邻居，而离群点更可能有不同的邻居。因此，RMBI 集群中的相对运动应该在许多重复的内部匹配之间，而 RMWO 集群中的相对运动更可能是不同的匹配。对于重复的推定匹配，RMBI 簇对应的推定匹配列表应该比由不同推定匹配组成的 RMWO 簇更有序。具有最小熵的假定匹配列表应该更有序。因此，具有MRME的相对运动簇被确定为由RMBI组成的簇。

随着视点变化和局部变形，一些内点的相对线性运动和相对角运动可能不在高点密度的连续区域内。在图 3(b) 和 © 中，可以看出并非所有真正的 RMBI 都包含在 MRME 集群中。然而，很明显，运动越接近簇$C_{min}$的中心，向量就越有可能被认为是 RMBI。因此，围绕 MRME 簇中心的一定半径内的相对运动被认为是重合相对运动。

给定集群$C_{min}$中的样本$c_{ij}=(s_{ij},r_{ij})$，$C_{min}$的平均线性运动$\bar{s}_{min}$和平均角运动$\bar{r}_{min}$定义为

$\bar{s}_{min}=mean(S_{min})\\ \bar{r}_{min}=mean(R_{min})\tag{8}$

其中$S_{min}=\{s_{ij}|c_{ij}\in C_{min}\}$，$R_{min}=\{r_{ij}|c_{ij}\in C_{min}\}$。$(\bar{s}_{min},\bar{r}_{min})$以簇$C_{min}$为中心。

然后，具有假定 RMBIs 的相对运动簇$C^*$定义为

$C^*=\{c_{ij}|d(c_{ij},\bar{c})<\rho,i,j\in\{1,2,...,N\}\}\tag{9}$

其中$\rho$是确定假定 RMBIs 的半径，$d(c_{ij},\bar{c})$是$c_{ij}$到$\bar{c}= (\bar{s}_{min},\bar{r}_{min})$的距离

$d(c_{ij},\bar{c})=\sqrt{(s_{ij}-\bar{s}_{min})^2+(r_{ij}-\bar{r}_{min})^2}\tag{10}$

在图 3（d）中，从集群$C_{min}$的中心到 RMBI 和 RMWO 的距离分别以蓝色和红色表示，按升序排列。很明显，大多数RMBI都在c周围的圈ρ内，而大多数RMWO都在圈外。因此，ρ 的默认值设置为 0.5。

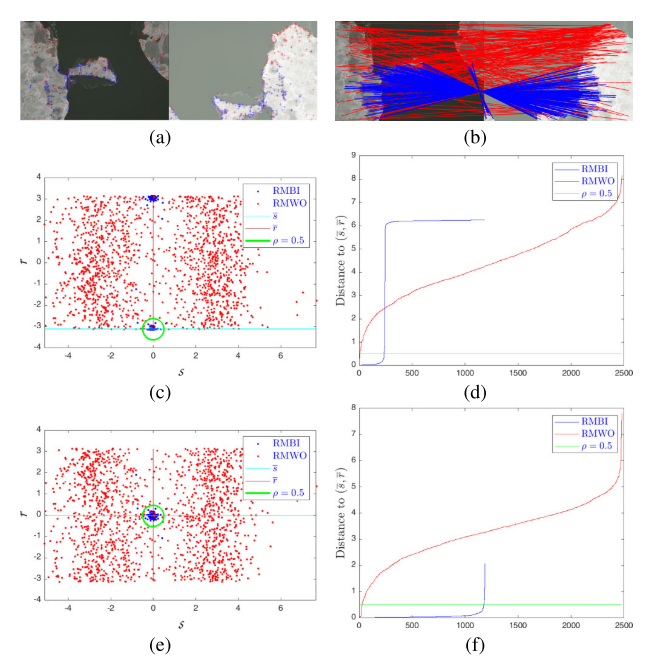
图4. 两个典型海冰图像对的点匹配结果。蓝色线和点代表正确匹配，红色线和点代表错误匹配。 (a) 和 (b) 特征点和假定的匹配。调整后旋转 π 或 -π 和 (e) 和 (f) 的两个图像的相对运动分布 © 和 (d)。

如图4©所示，当两幅图像旋转接近π或-π的角度时，RMBI可能被分成两部分；因此，一些匹配的边缘可能会被用于 RMWO。在图 4(e) 中，如果平均相对角运动$r_{min}$在 π/2 或 -π/2 附近，则相对角运动转换为

$r_{ij}= \begin{cases} r_{ij}-\pi,&r_{ij}\geq 0\\ r_{ij}+\pi,&r_{ij}< 0 \end{cases}\tag{11}$

图4（d）和（f）分别显示了RMBIs和RMWOs到$C_{min}$中心的距离，分别对应于图4（b）和（e）。转换后，大多数 RMBI 都在$\bar{c}$周围的半径 ρ = 0.5 内。

算法 1 给出了基于 MRME 确定假定的 RMBI 集群$C^*$的过程。给定假定的匹配 P 和 Q，计算相对运动 S 和 R。评估每个运动簇的RME，得到MRME簇$C_{min}$。如果$r_{min}$紧邻 π 或 -π，则 R 由 (11) 更新，$C_{min}$被更新，得到$C^*$。基于簇$C^*$中的相对运动，特征点被鲁棒和准确地匹配。

3.3 具有最小相对运动熵的特征匹配

基于RME，特征匹配被公式化为一个问题，以找到相对运动保持在MRME簇周围半径ρ内的特征

$\mathcal{I}^*=\arg\min_{\mathcal{I}}E(\mathcal{I};P,Q,\lambda)\tag{12}$

其中$\mathcal{I}$是内点集。基于 MRME 集群周围的相对运动，成本函数 E 定义为

$E(w;P,Q,\lambda,\rho)=\sum_{i=1}^N w_i(e_i-\lambda)+\lambda N\tag{13}$

其中$w_i$是第 i 个假定匹配$(p_i,q_i)$的匹配正确性

$w_i= \begin{cases} 1,&e_i\leq \lambda\\ 0,&e_i>\lambda,i=1,...,N \end{cases}\tag{14}$

其中$e_i$是假定匹配$(p_i,q_i)$与其对应的邻居之间的相对运动与 MRME 聚类一致的程度，并且

$e_i=\frac{1}{2K}\sum_{j|p_j\in N_{p_i}\ or\ q_j\in N_{q_i}}m(c_{ij}),c_{ij}\in C^*\tag{15}$

其中$m(c_{ij})$表示相对运动$c_{ij}$是否是相对运动簇$C^*$的成员

$m(c_{ij})= \begin{cases} 0,&d(c_{ij},\bar{c})\leq\rho\\ 1,&d(c_{ij},\bar{c})>\rho \end{cases}\tag{16}$

最优内点集$I^*$是

$\mathcal{I}^*=\{i|w_i=1,i=1,..,N\}\tag{17}$

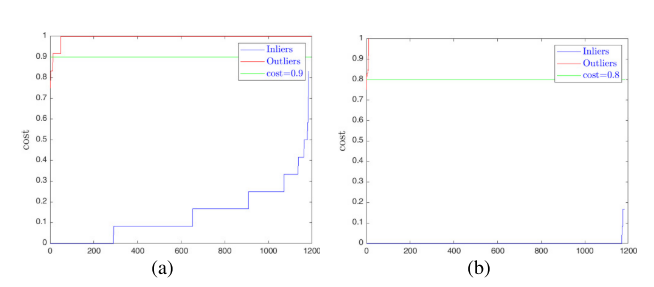
图5. 公式(15) 中成本 ei 的分布。 (a) 和 (b) 分别在$I_0$中所有假定匹配和假定匹配的成本。蓝线表示异常值的成本，而红线表示异常值的成本。

图 5 显示了图 1 中图像对的假定匹配的成本分布。图 5(a) 显示了所有假定匹配的成本，其中大多数异常值的成本（红色）大于 0.9，并且内线的成本（蓝色）小于 0.9。通过设置 λ = 0.9，大多数异常值被删除。在图 5(b) 中，异常值和内部值之间的成本差异被放大了。当 λ = 0.8 时，很容易去除剩余的异常值。

基于具有局部相对运动一致性的相对运动，点匹配方法设计为算法2，其中应用两次迭代去除异常值。在每次迭代中，首先计算相对运动，并通过算法 1 确定 MRME 簇$C^*$，从而获得重合的相对运动。每个假定匹配的成本是根据$C^*$中的相对运动计算的。用 λ 过滤后，可以准确、稳健地去除异常值。

3.4 计算复杂度

使用K-D树，KNN搜索每个特征点的时间复杂度为O((K+N) log N)。 DBSCAN 的时间复杂度约为 O(N(K + log N))。用 (7) 计算运动熵需要 O(N) 复杂度。

因此，在步骤 4 和 8 中计算成本$\{e_i\}_{i=1}^N$的时间复杂度约为 O(KN(K+log N))。异常值的确定具有 O(N) 时间复杂度。因此，MRME 的总时间复杂度约为 O(KN(K + log N))。 MRME存储每个点对的KNN邻居的空间复杂度约为O(KN)。由于K远小于N，我们方法的时间和空间复杂度可以简化为O(N log N)和O( N）。

结论

我们提出了一种新的基于相对运动一致性的特征匹配算法MRME。基于假定匹配与其 KNN 之间的相对运动，定义相对线性运动和角运动以评估局部相对运动的一致性。点匹配问题被视为相对运动一致性问题。为了从相对运动聚类结果中找到重合的相对运动，定义了 RME。基于与MRME的相对运动，设计了两阶段的特征匹配策略。在三个航空数据集上进行测试，平均 F 分数表明 MRME 在召回率和精度之间取得了最佳平衡。与十种典型的特征匹配方法相比，可以得出结论，MRME在匹配具有重异常值和伪同构结构的特征方面更加稳健和准确。