LSCC：基于局部结构一致性约束的判别点匹配算法

LSCC：基于局部结构一致性约束的判别点匹配算法(2020)

摘要：

由于遥感图像中存在重复模式、模糊特征和相似的局部结构，不可避免地保留具有局部伪同构结构的离群点作为内联线，这使得点匹配仍然是一个具有挑战性的问题。为了提高特征匹配的准确性，提出了一种称为局部结构一致约束的判别点匹配算法，以去除假设对应中的异常值，并找到由内联线组成的两个局部结构一致图。首先，提出了一种局部结构描述符来评估K近邻的相应结构相似性。然后，定义了一个代价函数来评估局部结构的一致性。采用两阶段离群点消除策略，消除具有不同局部结构的特征点，得到两个局部结构一致图。为了评估该算法的性能，使用了在山东半岛周围拍摄的具有重复局部模式和模糊特征的45对航空图像。与五种最先进的点匹配方法相比，该算法被证明更准确、更高效。

关键词：图像配准、局部结构相似性、点匹配。

1. 引言

区域匹配用于从具有重叠区域的两幅图像中找到两个点集之间的最佳对应，广泛应用于图像配准、目标跟踪和变化检测。通常，假设的对应关系首先通过比较特征描述符的相似性来构建。然后，进一步去除异常值。为了提高精度和效率，分别研究了特征描述符和孤立点去除方法。

基于尺度不变特征变换（SIFT）[1]，研究了遥感图像处理中的众多特征描述符[2]-[4]。Dellinger等人[5]提出了一种类似SIFT的算法，称为SAR-SIFT。马等人[2]使用SAR-SIFT算子改进了相位一致性图像的特征检测。吴等人[3]使用基于相位一致性的归一化互相关来去除明显的异常值，然后使用全局结构来增加更正确的对应。这些方法提高了特征描述符在特定图像（如SAR图像）上的性能。各种遥感图像的公共特征描述符仍然是一个有待研究的问题。

另一方面，由于重复局部模式和模糊特征的存在，在假定的对应中不可避免地保留了错误匹配。因此，除了改进特征描述符外，还提出了许多异常值去除方法。通常，离群点去除方法可以分为两类：依赖几何变换模型的算法和基于局部结构相似性的算法。基于几何变换模型的最著名方法是随机样本一致性（RANSAC）算法[6]，该算法从随机选择的数据集子集估计数学模型，然后在规定的迭代次数内消除异常值。RANSAC的匹配结果高度依赖于随机选择的初始子集。基于软分配、确定性退火和薄板样条，Chui和Rangarajan[7]构建了通用框架薄板样条鲁棒点匹配（TPS-RPM）。马等人[8]将局部几何约束引入特征匹配的最大似然公式，提出了一种局部线性变换（LLT）框架，用于刚性、仿射和非刚性特征匹配。基于SIFT特征之间的两个最近邻距离比（NNDR），吴等人[9]提出了快速样本一致性（FSC），以提高RANSAC的可靠性和效率。从具有高正确率的对应集和由小NNDR获得的少量正确匹配中采样，确定变换模型参数，并用于从由大NNDR获得的对应集中找到最大一致集。粒子群优化样本一致性（PSOSC）[10]不是随机选择临时匹配，而是直接对模态变换参数进行采样，这使得其对正确率的敏感性低于RANSAC。理论上，基于几何模型的方法将获得高精度，但在实践中，转换模型的精度取决于初始点集。当初始对应中存在许多异常值时，匹配结果可能不够稳健。此外，反复估计变换模型会使这些算法耗时且效率较低。

为了准确、稳健地匹配特征点，人们提出了许多基于局部结构一致性的方法。Aguilar等人[11]通过K-最近邻（KNN）平均距离过滤，提出了一种称为图变换匹配（GTM）的算法，以消除可疑匹配并获得一致图。由于存在异常值，平均距离不可靠，这可能导致匹配结果中出现大量异常值。将对应KNN的空间顺序视为两个字符串，并与循环字符串匹配方法进行比较，刘等人[12]提出了一种称为受限空间顺序约束（RSOC）的算法。通过建立特征之间的几何（角度距离）关系，Izadi和Saeedi[13]提出了一种改进的GTM，称为加权图变换匹配（WGTM）。这些方法虽然试图通过局部结构约束提高特征匹配的准确性，但效率不高。基于几何约束，马等人[8]、[14]、[15]提出了许多方法。在这些方法中，局部保持匹配（LPM）[15]是最具代表性的：它简洁、鲁棒，并且能够有效地去除虚假匹配。基于两幅图像中两个对应特征点之间的长度比和向量角度，邻域拓扑的一致性被定义为过滤掉特征点之间具有不同空间邻域结构的匹配的代价。通过利用局部邻域结构的一致性，提出了一种基于学习的方法，称为不匹配消除学习（LMR）[14]，该方法将不匹配消除表述为两类分类问题。所有这些算法都依赖于局部结构相似性来找到两个具有相似结构的一致KNN图。姜等人[16]将特征匹配视为一个带有离群值的空间聚类问题，提出了使用空间聚类的鲁棒特征匹配（RFM-SCAN）。在不估计转换模型的情况下，这些方法应该更稳健。然而，由于图像中存在重复模式和模糊特征，当孤立点周围的局部结构相似时，现有算法难以识别局部伪同构结构。异常值将不可避免地保留为匹配点，这将影响匹配结果的准确性。受线性规划的启发，提出了一种快速、有区别的特征匹配算法，以解决局部伪同构结构特征的失配问题，提高点匹配算法的效率和准确性。在该算法中，定义了局部结构描述符（LSD）来评估局部结构一致性。基于局部结构一致性约束（LSCC），设计了一种两阶段孤立点去除策略。该算法不需要每次迭代中的变换估计和点变换，因此更高效、更准确。

这篇文章的其余部分组织如下。第二节介绍了所提出的描述符和匹配策略。第三节给出了实验结果和性能分析。第四节得出了结论。

2. 提出的方法

2.1 LSD

由基于SIFT的特征检测器从两个仿射变换图像中提取，两个点集$P=\{p_1,p_2,..,p_i,..,p_n\}$和$Q=\{q_1,q_2,..,q_i,..,q_n\}$是初始对应点。由于点周围小区域内的物理约束[15]，特征点之间的局部邻域结构可能不会自由变化，这意味着在变换后应保持匹配对应的局部结构。如图1（a）所示，由正确匹配及其最近邻组成的局部结构是重合的，而图1（b）中由错误匹配及其最近邻组成的局部结构是不规则变化的。因此，异常值的相应局部结构将是不同的，而由内联线组成的局部结构应该是重合的。基于这一思想，将假设点对与其KNN之间的欧几里德距离定义为LSD，以评估局部结构一致性。

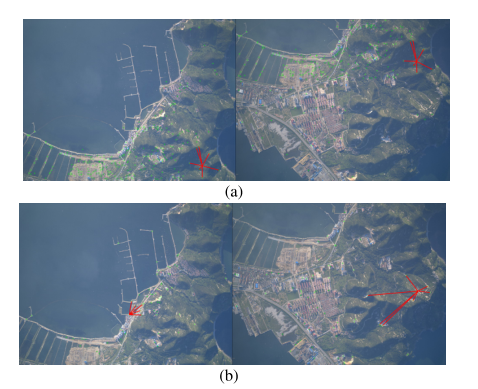
图1. 局部结构演示。（a）正确匹配的局部结构。（b）虚假匹配的局部结构。

如图2所示，具有八个公共邻域的点对$p_i,q_i$的LSD定义为 $D_p(i)=\{d(p_i,p_j)|p_i,p_j\in P,p_j\in N_{p_i}\},D_q(i)=\{d(q_i,q_j)|q_i,q_j\in Q,q_j\in N_{q_i}\}$，其中$d(p_i,p_j)$是$p_i$和它的邻居$p_j$之间的欧几里得距离，$d(q_i,q_j)$是$q_i$和它的邻居$q_j$之间的欧几里得距离，

$N_{p_i}\ and\ N_{q_i}$是$p_i,q_i$的邻域。

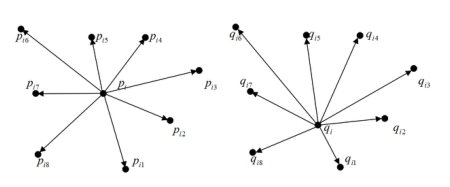
图2. LSD示意图。

基于简单的几何直觉，两个点集的入口之间的局部距离预计将在几乎相同的尺度上变化，并且高度相关。 因此，$D_p(i)$和$D_q(i)$之间的相关系数用于评估假设对应点对$(p_i,q_i)$周围的局部结构一致性$s(p_i,q_i)$，如下所示：

$s(p_i,q_i)=\Big(0.5-corrcoef(D_p(i),D_q(i))^2\Big)*m\tag{1}$

其中m是公共邻域数，corrcoef是皮尔逊相关系数函数，$D_p(i)$和$D_q(i)$是pi和qi与其公共邻域之间的欧几里得距离。根据两个向量X和Y，相关系数定义如下：

$\begin{aligned} corrcoef(X,Y)&=\frac{\sum_{i=1}^n(x_i-\bar{x})(y_i-\bar{y})}{\sqrt{\sum_{i=1}^n(x_i-\bar{x})^2}\sqrt{\sum_{i=1}^n(y_i-\bar{y})^2}}\\ &=\frac{cov(X,Y)}{\sigma_X\sigma_Y} \end{aligned}\tag{2}$

其中，$n，cov(X，Y)，σ_X，σ_Y$分别是X和Y的长度、协方差和标准差。

受局部结构一致性$s(p_i,q_i)$的约束，具有重合局部结构的假定对应点将被保存，而具有不同局部结构的对应点将被惩罚和删除。当公共邻域数小于3时，相关系数不能用于评估局部结构一致性。在这种情况下，s将设置为零。

2.2 问题公式化

为了匹配两个假定的对应点集P和Q，建立了2个KNN图$G_P$和$G_Q$。如果P和Q完全匹配，则$G_P$和$G_Q$的结构应相互吻合。因此，特征匹配被定义为找到两个局部结构一致图，可以通过

$I^*=\arg\min_I C(I;S)\tag{3}$

其中$I$是具有最大同构图和最小局部结构差的内联集。 S是假定的对应关系，表示为$S=\{(p_i,q_i)|i\in N,p_i\in P,q_i\in Q\}$，其中N是P和Q的大小。代价函数定义如下：

$C(I;S)=\sum_{i\in I}(t(p_i,q_i)+s(p_i,q_i))\tag{4}$

其中$t(p_i,q_i),s(p_i,q_i)$是邻域拓扑一致性和局部结构一致性的约束。基于$p_i,q_i$之间的邻域差，$t(p_i,q_i)$定义如下：

$t(p_i,q_i)=\sum_{j|p_j\in N_{p_i}}n(p_i,p_j)\tag{5}$

这里，$n(p_i,p_j)$是LPM中的邻域差，如下所示：

$n(p_i,p_j)= \begin{cases} 0,&p_j\in N_{p_i},&q_j\in N_{q_i}\\ 1,&p_j\in N_{p_i},&q_j\notin N_{q_i} \end{cases}\tag{6}$

利用邻域拓扑一致性约束$t(p_i,q_i)$，去除具有不同邻域的孤立点。与马的LPM[15]不同的是，（1）中的LSCC $s(p_i,q_i)$用于寻找具有伪同构局部结构的异常值。为了解决优化问题并获得两个最大局部结构一致图，设计了一种两阶段异常值去除策略。

2.3 异常值消除策略

基于LSD和代价函数，算法1设计并概述了一种两阶段异常值去除策略。在每个阶段中，首先用假设的对应关系构建两个KNN图。然后，在计算每个假设对应的成本后，将成本大于阈值的对应作为异常值并删除。重复这些步骤，直到所有通信的成本低于给定阈值。在第一阶段，使用大阈值$\lambda_1$。消除了具有不同邻域和很少公共邻域的异常值。得到了具有相似局部结构的假定对应关系。然后，在第二阶段，应用小阈值$\lambda_2$。在局部结构一致性的约束下，去除伪同构结构的假设对应，得到两个局部结构一致性图。

2.4 复杂度分析

使用K-D树，KNN搜索每个特征点的时间复杂度为$(O((K+N)logN))$。要计算C，时间复杂度约为$O(kn)$。更新内联集$I$需要$O(N)$复杂度∗. 在最坏的情况下，LSCC将在不超过十次迭代内停止。因此，LSCC的总时间复杂度应为$(O(NlogN))$。为了存储最近邻，空间复杂度约为$O(kn)$。

3. 实验与分析

在实验中，使用了山东半岛周围采集的45对典型航空图像对来评估该算法的性能。由于这些图像中存在重复模式、模糊特征和相似的局部结构，特征点匹配具有挑战性。图像大小调整为1000×753像素。在每个图像对中平均检测到大约1100个假定对应。VLFEA T工具箱用于生成假定的对应点对并搜索KNN。所有算法均在2.800 GHz CPU和8 GB内存的Intel i5-6200U上以MA TLAB编写和执行。在本节中，将该算法与其他五种特征匹配方法进行了比较，即WGTM、RANSAC、GTM、LPM和RSOC。首先给出了定性匹配结果。然后，对45个结果进行了定量比较。准确性、精密度、召回率、特异性[11]和均方根误差（RMSE）[12]被用作评估性能的标准。阈值λ1设置为0.9，而λ2设置为0.5。为了构建KNN图，将k设置为8。为了计算相关系数，至少需要四个公共邻域。在RSOC、LPM、GTM和WGTM的情况下，默认参数与文献中的参数相同。