LPM：局部保持匹配

LPM：局部保持匹配（2019）

摘要：

在两个特征集之间寻求可靠的对应关系是计算机视觉中一项基本而重要的任务。本文试图从给定的假定图像特征对应中去除不匹配。为了实现这一目标，设计了一种称为局部保持匹配（LPM）的有效方法，其原理是保持那些潜在真实匹配的局部邻域结构。我们将问题表述为数学模型，并推导出具有线性时间和线性空间复杂度的封闭形式的解决方案。我们的方法可以在几毫秒内完成从数千个假定对应关系中去除不匹配。为了证明我们处理图像匹配问题的策略的普遍性，对用于一般特征匹配的各种真实图像对以及点集配准、视觉归巢和近似重复图像检索进行了广泛的实验。与其他最先进的替代方案相比，我们的 LPM 在准确度方面实现了更好或具有竞争力的性能，同时将时间成本大幅降低了两个数量级以上。

关键词：特征匹配 · 图像配准 · 局部性保留 · 刚性和非刚性变换 · 异常值去除

1.引言

本研究的重点是在同一场景的两幅图像之间建立可靠的点对应关系。许多计算机视觉任务，例如 3D 重建、基于内容的图像检索、视觉归巢、图像拼接、图像配准和融合，都是从假设点对应已成功恢复开始的（Bian et al. 2017; Lin et al. 2018 ;steel 2013）。在本文中，我们将目标任务视为两组离散点之间的匹配问题，其中每个点都是由特征检测器提取的图像特征，并具有局部图像描述符，例如尺度不变特征变换 (SIFT) (Lowe 2004)。

匹配问题具有组合性质，匹配空间巨大。即使不考虑异常值，将 N 个点与另一个 N 个点匹配的简单问题也会导致总共 N！排列（Wang et al. 2014）。为了减轻计算压力，一种流行的策略是通过施加相似性约束来构建一组假定的对应关系，以减少可能的匹配数量。它要求点只能匹配具有相似描述符的点。在这种情况下，匹配任务归结为确定假定集中每个匹配的正确性。

在过去的几十年中，已经开发了各种稳健的估计器来解决失配消除问题。尽管如此，为实际使用定制有效且高效的算法仍然具有挑战性。挑战主要来自三个方面。首先，仅使用局部描述符信息将不可避免地导致假定集中出现大量错误匹配，如果图像对遭受低质量、遮挡、重复结构等问题，这个问题通常会更加严重。其次，两幅图像之间的变换模型多种多样，很难设计出通用的算法。然而，在许多计算机视觉任务中通常需要这种通用算法，例如可变形物体识别，其中变换模型是预先未知的。第三，高计算量，特别是当两幅图像之间的几何变换是未知的复杂非刚性模型时，限制了其在实时任务中的适用性。

为了解决上述三个挑战，本文提出了一种简单但非常有效的特征匹配方法，它能够在几毫秒内准确地从假定的对应集中去除异常值。我们观察到，对于同一场景或物体的图像对，在视点变化或非刚性变形下，两个特征点之间的绝对距离可能会发生显着变化，但表示图像场景拓扑结构的特征点之间的空间邻域关系通常很好由于物理限制而保留。基于这一观察，我们引入了一个数学模型，旨在将未知的内部对应关系约束为具有相似的局部邻域结构。该模型是通用的，它可以包含刚性和非刚性变形。我们进一步推导出了一个简单的闭式解，它相对于给定的假定集合的规模具有线性时间复杂度和线性空间复杂度。对各种图像数据的定性和定量实验表明，与其他最先进的方法相比，所提出的方法可以用更少的计算时间（快两个数量级以上）产生更准确的匹配结果。

更具体地说，本文的贡献可以总结如下：

我们提出了一种简单而有效的鲁棒特征匹配方法。与大多数需要特殊参数或非参数模型来表征全局图像变换的现有方法不同，我们的方法仅旨在保留特征点的局部邻域结构，因此更通用。

我们推导出了一个具有线性复杂度的封闭形式的解决方案，它可以在几毫秒内解决一个具有大约 1000 个假定对应关系的典型匹配问题。这对许多实时应用程序是有益的，并且可以为复杂的特定问题匹配算法快速提供良好的初始化。

我们将我们的方法应用于几个视觉任务，包括点集配准、视觉归航和近似重复图像检索，并设计相应的方法。我们在公开可用的数据集上验证了所提出的方法，并在准确性和效率方面获得了比其他最新方法更好的结果。

这份手稿的初步版本出现在 Ma 等人的文章中（2017）。主要的新贡献包括以下四个方面。首先，我们提供了所提出方法的扩展推导，并提供了更多细节。其次，我们对公式进行了概括并给出了空间邻域关系的综合定义，这可以进一步提高匹配性能。第三，我们将所提出的方法应用于几个视觉任务，并详细设计了相应的算法。最后，我们对更具挑战性的数据集进行了广泛的实验，并与更先进的方法进行了比较。为了让社区进行更多比较并鼓励未来的工作，我们发布了我们的代码。

本文的其余部分安排如下。第 2 节描述了背景材料和相关工作。第三节，我们提出了我们的局部保留匹配，以实现鲁棒的特征匹配。我们将我们的方法应用于几个视觉任务，并在第四节中设计了相应的方法。第5节说明了我们的方法在不同视觉任务上与其他方法相比的性能，然后是第6节中的一些结论性评论。

2.相关工作

特征匹配已广泛应用于许多领域，包括计算机视觉（Torr and Zisserman 2000；Jiang et al. 2017）、模式识别（Gao et al. 2017；Guo and Cao 2012）、医学图像分析（Ma et al. 2017；Wang et al. al. 2016）、遥感（Ma et al. 2015; Yang et al. 2017）、机器人技术（Liu et al. 2013; Zhao and Ma 2017）等。这里我们简要回顾一下作为当前参考的背景材料学习。该材料包括两种方法类型：第一种类型建立一组假定的对应关系，然后删除错误匹配，而第二种类型解决几个点集之间的对应关系矩阵。

2.1 基于两步策略的方法

解决匹配问题的流行策略包括两个步骤（Ma et al. 2014）：首先计算一组假定的对应关系，然后通过几何约束去除异常值。在第一步中通过修剪所有可能的点匹配集来获得假定的对应实例。这种情况是通过计算点处的特征描述符并消除描述符过度不同的点之间的匹配来实现的。 Lowe (2004) 提出了带有距离比方法的 SIFT 描述符，该方法将最近邻和次近邻之间的比率与预定义的阈值进行比较，以过滤掉不稳定的匹配。 Guo 和 Cao (2012) 提出了三角形约束，与 Lowe (2004) 中的距离比相比，它可以在数量和准确性方面产生更好的假定对应关系。 Pele and Werman (2008) 应用推土机距离代替 Lowe (2004) 中的欧几里得距离来衡量描述符之间的相似性并提高匹配精度。此外，胡等人2015 年在假定的对应构建过程中采用了为每个特征点选择合适的描述符的局部选择，而不是使用全局描述符。已经提出了级联方案来防止丢失真实匹配，这可以显着提高对应数量（Wang et al. 2014 ; 赵和李 2012)。尽管已经有各种复杂的方法来构建假定匹配，但仅使用局部外观特征将不可避免地导致大量错误匹配。第二步，使用基于一些几何约束的鲁棒估计器来检测和去除异常值。

为了从假定的集合中去除错误匹配，在过去的几十年中已经开发了许多方法，大致可以分为四类，比如统计回归方法、重采样方法、非参数插值方法和图匹配方法。统计文献表明，与二次 L2 范数相比，最小化 L1 范数的方法更稳健，并且可以抵抗更大比例的异常值（Huber 1981）。刘等人2015 年提出了一种基于自适应增强学习的回归方法，用于 3D 刚性匹配。最近，迈尔等人2016 年引入了一种基于统计光流的引导匹配方案，并在准确性和效率方面都取得了可喜的成果。最流行的重采样方法是随机样本共识 (RANSAC)，它有多种变体，例如 MLESAC (Torr and Zisserman 2000) 和 PROSAC (Chum and Matas 2005)。这些方法采用假设和验证方法，并尝试获得最小的无异常值子集，以通过重采样来估计提供的参数模型。统计回归和重采样方法依赖于预定义的参数模型，当底层图像转换为非刚性时，其效率会降低；如果异常值比例变大，这些方法也往往会严重退化（Li and Hu 2010）。最近引入了几种非参数插值方法来解决这些问题，包括识别对应函数 (ICF) (Li and Hu 2010)、有界失真 (BD) (Lipman et al. 2014)、向量场一致性 (VFC) (Ma et al. 2014) 和鲁棒点匹配与流形正则化 (MR-RPM) (Ma et al. 2017; Wang et al. 2016)。这些方法通常通过应用先验条件来插入非参数函数，其中与特征对应相关的运动场是缓慢而平滑的。然而，它们通常具有三次复杂性，并且对于大型假定集合而言计算成本巨大，这限制了它们在实时任务中的适用性。图匹配是解决匹配问题的另一种技术。一些具有代表性的研究包括光谱匹配（Leordenu 和 Hebert 2005）、对偶分解（Torresani 等人 2008）、模式搜索（Wang 等人 2014；Cho 和 Lee 2012）、图位移（GS）（Liu 和 Yan 2010） , 和离散禁忌搜索 (Adamczewski et al. 2015)。图匹配为转换模型提供了相当大的灵活性，并提供了强大的匹配和识别。然而，它也有类似的非多项式难性质的缺点。从技术上讲，我们的工作属于这一类。

除了上述方法之外，我们还想强调两个最近提出的重要算法，它们将分段平滑约束结合到匹配中。第一个是一种非线性回归技术，称为基于一致性的决策边界（Lin et al. 2014, 2013, 2018）。该算法旨在从高噪声匹配中发现基于一致性的可分离性约束，并将其嵌入到对应似然模型中，然后通过变化仿射运动模型获得准确匹配。它能够在宽基线上产生高质量的匹配，并且对大量异常值（甚至高达 90%）具有鲁棒性。第二个是基于网格的运动统计 (GMS) (Bian et al. 2017)，它通过将运动平滑度约束转换为基于相邻匹配数量的统计度量来去除异常值。该算法的一个主要优点是它开发了一个有效的基于网格的分数估计器，可以提供实时、超鲁棒的特征对应，因此对视频应用很有好处。

2.2 基于对应矩阵的方法

另一种策略是将对应矩阵与参数或非参数几何约束结合起来。在这种情况下，特征点通常没有局部图像描述符的信息。最著名的点匹配方法之一是迭代最近点 (ICP) (Besl and McKay 1992)ICP利用最近邻关系替代地分配二进制对应；然后它通过估计的对应关系执行最小二乘变换估计，直到达到局部最小值。 Chui 和 Rangarajan (Chui 和 Rangarajan 2003) 建立了一个非刚性匹配的通用框架，称为薄板样条稳健点匹配 (TPS-RPM)，它在连续优化框架内用软分配替换 ICP 的最近点策略，包括确定性退火。杨等人 (Yang et al. 2015) 进一步介绍了一种称为薄板样条的全局和局部混合距离的方法，并取得了可喜的成果。 Zheng 和 Doermann 提出了一种基于图的鲁棒点匹配方法，该方法基于保留局部邻域结构 (RPM-LNS) (Zheng and Doermann 2006)。 Boughorbel 等人 (Boughorbel et al. 2004) 将高斯场引入了刚性配准，后来在 Ma 等人中推广到非刚性设置（2015 年）和（Wang 等人2016 年）。近年来，点集配准通常通过概率方法解决，例如基于高斯混合模型的配准 (GMMREG) (Jian and Vemuri 2011)、相干点漂移 (CPD) (Myronenko and Song 2010) 及其变体 (Horaud et al . 2011; steel. 2016).这些方法将匹配问题表述为利用高斯混合模型对混合密度的估计，这是在最大似然框架和期望最大化算法中解决的。然而，由于这些方法完全丢弃了局部图像描述符的丰富信息，它们的匹配性能很可能会下降，尤其是当图像对涉及非刚性变形时（Ma et al. 2016）。

3. 方法论

本节描述了我们在分别从相同或相似场景的两个图像中提取的两个特征集之间建立准确对应关系的方法。为此，我们首先通过考虑两个特征集之间所有可能的匹配并过滤掉特征描述向量足够不同的匹配来构建一组假定的匹配。然后，我们使用几何约束来删除假定集中包含的错误匹配，从而进一步过滤掉特征点之间具有不同空间邻域结构的匹配。幸运的是，有几个设计良好的特征描述符（例如，SIFT Lowe2004）可以有效地建立特征集之间的假定对应关系，因此，我们认为这个组件是一个简单的任务。在下文中，我们专注于失配消除问题。

3.1 问题表述

我们假设已经从给定的两幅图像中提取出了$N$对假定对应特征$S=\{(x_i,y_i)\}_{i=1}^N$，其中 xi 和 yi 是表示特征点空间位置的 2D 列向量（我们的方法不受输入数据维度的限制，可以直接应用于 3D 匹配问题）。我们的目标是去除 S 中包含的异常值以建立准确的对应关系。

3.1.1 理想刚体变换的公式

如果图像对之间的空间关系是简单的刚性变换，那么任何特征对应之间的距离都会被保留。换句话说，表示未知的内点集，它的最优解是

$\mathcal{I}^*=arg\min_\mathcal{I}{C(\mathcal{I};S,\lambda)}\tag{1}$

成本函数 C 定义为：

$C(\mathcal{I;S,\lambda})=\sum_{i\in\mathcal{I}}\sum_{j\in\mathcal{I}}(d(x_i,x_j)-d(y_i,y_j))^2+\lambda(N-|\mathcal{I}|)\tag{2}$

其中 d 是某个距离度量，例如欧几里得距离，|·|表示集合的基数。在这个成本函数中，第一项惩罚任何不保留点对距离的匹配，第二项阻止异常值，参数 λ> 0 平衡这两项。理想情况下，最优解应该实现零惩罚，即 C 的第一项应该为零。

3.1.2 一般特征匹配的公式

然而，在现实世界的场景中，刚性转换几乎不是这种情况。例如，如果图像对进行了相对复杂的非刚性变换，上述距离关系将不再成立，尤其是对于彼此相距较远的匹配。然而，由于点周围小区域的物理约束，特征点之间的局部邻域结构可能不会自由改变，这意味着应该保留变换后的相邻点对的分布（Zheng and Doermann 2006）。接下来，通过仅保留局部结构，方程式(2)中的成本函数变为：

$C(\mathcal{I};S,\lambda)=\sum_{i\in\mathcal{I}}\frac{1}{2K}\bigg(\sum_{j|x_j\in\mathcal{N}_{x_i}}(d(x_i,x_j)-d(y_i,y_j))^2+\\\sum_{j|y_j\in\mathcal{N}_{y_i}}(d(x_i,x_j)-d(y_i,y_j))^2\bigg)+\lambda(N-|\mathcal{I}|)\tag{3}$

其中**$\mathcal{N}_x$表示点 x 的邻域**。点集没有明显的邻域定义。在我们的评估中，我们采用了一种简单的策略，即在欧几里得距离下为相应特征集中的每个点搜索 K 个最近邻。请注意，我们在等式 (3) 的第一项中使用 1/2K对邻域中每个元素的贡献进行归一化。

我们将假定的集合 S 与 N×1 二元向量 p 相关联，其中 pi ∈{0, 1} 表示第 i 个对应关系 (xi, yi) 的匹配正确性。具体来说，pi = 1 表示内部值，否则表示异常值。请注意，在非刚性变形（例如比例变化）下，点对的绝对距离不能很好地保持。为了解决这个问题，我们将距离量化为两个级别：

$d(x_i,x_j)= \begin{cases} 0,&x_j\in\mathcal{N}_{x_i}\\ 1,&x_j\notin\mathcal{N}_{x_i} \end{cases}, d(y_i,y_j)= \begin{cases} 0,&y_j\in\mathcal{N}_{y_i}\\ 1,&y_j\notin\mathcal{N}_{y_i} \end{cases}\tag{4}$

即$\sum_{j|x_j\in\mathcal{N}_{x_i}}(d(x_i,x_j)-d(y_i,y_j))^2$表示在x邻域但不在y邻域的个数。

命题 1：用等式 (4)中的距离定义，等式 (3) 中的成本函数等价于以下最小化问题：

$C(\mathbb{p};S,\lambda)=\sum_{i=1}^N\frac{p_i}{K}\sum_{j|x_j\in\mathcal{N}_{x_i}}d(y_i,y_j)+\lambda\bigg(N-\sum_{i=1}^N p_i\bigg)\tag{5}$

证明：通过使用方程式（4）中定义的距离和一个二元向量$\mathbb{p}$，方程式（3）中的成本函数变为：

$C(\mathbb{p};S,\lambda)=\sum_{i=1}^N\frac{p_i}{2K}\bigg(\sum_{j|x_j\in\mathcal{N}_{x_i}}d(y_i,y_j)\\ +\sum_{j|y_j\in\mathcal{N}_{y_i}}d(x_i,x_j)\bigg)+\lambda\bigg(N-\sum_{i=1}^N p_i\bigg)\tag{6}$

我们考虑项$\sum_{j|x_j\in\mathcal{N}_{x_i}}d(y_i,y_j)$:

$\begin{aligned} \sum_{j|x_j\in\mathcal{N}_{x_i}}d(y_i,y_j)&=\sum_{j|x_j\in\mathcal{N}_{x_i},y_j\in\mathcal{N}_{y_i}}d(y_i,y_j) +\sum_{j|x_j\in\mathcal{N}_{x_i},y_j\notin\mathcal{N}_{y_i}}d(y_i,y_j)\\ &=0+count(j|x_j\in\mathcal{N}_{x_i},y_i\notin\mathcal{N}_{y_i})\\ &=K-count(j|x_j\in\mathcal{N}_{x_i},y_j\in\mathcal{N}_{y_i})\\ &=K-n_i \end{aligned}\tag{7}$

其中 count(·) 计算集合中的元素个数，ni 表示两个邻域$\mathcal{N}_{x_i} 和 \mathcal{N}_{y_i}$中共有元素的个数。同样的，我们有：

$\sum_{j|y_j\in\mathcal{N}_{y_i}}d(x_i,x_j)=K-n_i=\sum_{j|x_j\in\mathcal{N}_{x_i}}d(y_i,y_j)\tag{8}$

通过将公式（8）代入公式（6），我们获得公式（5）的最小化问题

3.1.3 邻域拓扑一致

上面描述的最小化问题本质上旨在保留邻域的交集（例如，邻域元素的共识），这忽略了它们的拓扑结构。为了解决这个问题，我们在这里设计了一个成本来进一步利用邻域拓扑的共识。

对于假定匹配 (xi , yi )，我们首先提取其位于$\mathcal{N}_{x_i} 和 \mathcal{N}_{y_i}$的 ni 相邻假定匹配，其中 K = 5 和 ni = 3。接下来，我们将假定匹配转换为位移向量，其中每个向量的头尾对应于两幅图像中两个对应特征点的空间位置，与 (xi , yi ) 关联的向量用粗体突出显示，即 vi 。然后可以通过比较与 ni 个相邻假定匹配相关的 vi 和 v j 之间的差异来利用邻域拓扑。更具体地说，ni 元素关于 xi 和 yi 的拓扑结构的变化将导致 vi 和 v j 之间的显着差异长度和方向，如图 1 中的两个示例所示。

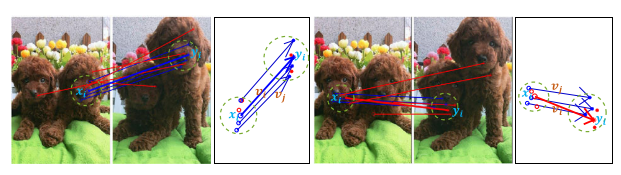
图1. 邻域拓扑共识的示意图。假定的匹配 (xi , yi )（用粗体突出显示）是左侧组中的内点和右侧组中的异常点。对于每个组，左图显示了一个假定的匹配 (xi , yi ) 及其邻域元素，它们对应的位移向量显示在右图中，vi 对应于 (xi , yi )

根据以上分析，我们根据 vi 和 v j 的长度比和夹角来定义邻域拓扑的一致性：

$s(v_i,v_j)=\frac{\min\{|v_i|,|v_j|\}}{\max\{|v_i|,|v_j|\}}\times\frac{(v_i,v_j)}{|v_i|\times|v_j|}\tag{9}$

其中$s(v_i,v_j)\in[-1,1]$值越大表示一致性越高，用$余弦相似度^{补充内容1}$来表征角度的一致性，(·,·) 表示内积。

根据方程式 (9) 并考虑到非刚性变形的问题，我们定义了 vi 和 v j 之间的量化距离，预定义的阈值 τ 如下：

$d(v_i,v_j)= \begin{cases} 0,&s(v_i,v_j)\geq \tau \\ 1,&s(v_i,v_j)< \tau \end{cases}\tag{10}$

有了上述距离并考虑方程式(5)中的最小化问题，我们得到一个新的目标函数：

$C(\mathbb{P};S,\lambda,\tau)=\sum_{i=1}^N\frac{p_i}{K}\bigg(\sum_{j|x_j\in\mathcal{N}_{x_i}}d(y_i,y_j)\\ +\sum_{j|x_j\in\mathcal{N}_{x_i},y_j\in\mathcal{N}_{y_i}}d(v_i,v_j)\bigg)+\lambda\bigg(N-\sum_{i=1}^N p_i\bigg)\tag{11}$

其中第一项括号内的值为0到K之间的整数。

3.1.4 多尺度邻域表示

在我们的公式中，我们建议搜索每个点 x 的 K 个最近邻，以构建其邻域$\mathcal{N}_x$。然而，由于以下两个原因，K 的最佳值可能会发生变化：i) 假定的匹配通常在图像域中分布不均匀，以及 ii) 异常值的比例随着不同假定集的变化而变化。因此，使用固定的 K 将无法解决一般的特征匹配问题。

为了解决这个问题，我们使用多尺度邻域表示并定义一组具有大小$\mathbb{K}=\{K_m\}_{m=1}^M$的邻域,例如，$\{\mathcal{N}_{x_i}^{K_m}\}_{m=1}^M$和$\{\mathcal{N}_{y_i}^{K_m}\}_{m=1}^M$，其中$\mathcal{N}_{x_i}^{K_m}$表示点 xi 的邻域，由其在欧几里得距离下的$K_m$最近邻组成。在这种情况下，方程 (11) 中的目标函数变成

$C(\mathbb{P};S,\lambda,\tau)=\sum_{i=1}^N\frac{p_i}{K}\sum_{m=1}^M\frac{1}{K_m}\bigg(\sum_{j|x_j\in\mathcal{N}_{x_i}^{K_m}}d(y_i,y_j)\\ +\sum_{j|x_j\in\mathcal{N}_{x_i}^{K_m},y_j\in\mathcal{N}_{y_i}^{K_m}}d(v_i,v_j)\bigg)+\lambda\bigg(N-\sum_{i=1}^N p_i\bigg)\tag{12}$

其中 1/M 用于归一化每个级别邻域的贡献。显然，方程式 (12) 中的最终目标函数是平移、旋转和尺度不变的。然后可以通过最小化方程 (12)来解决去除异常值和建立准确特征匹配的问题。

3.2 解决方案

为了优化目标函数（12），我们通过合并与 pi 相关的项来重新组织其形式，并获得：

$C(\mathbb{p};S,\lambda,\tau)=\sum_{i=1}^N p_i(c_i-\lambda)+\lambda N\tag{13}$

其中

$c_i=\sum_{m=1}^M \frac{1}{MK_m}\bigg(\sum_{j|x_j\in\mathcal{N}_{x_i}^{K_m}}d(y_i,y_j)\\+\sum_{j|x_j\in\mathcal{N}_{x_i}^{K_m},y_j\in\mathcal{N}_{y_i}^{K_m}}d(v_i,v_j)\bigg)\tag{14}$

测量第 i 个对应关系 (xi , yi ) 是否满足保留局部邻域结构的几何约束。显然，正确的匹配会带来零成本或较小的成本，而错误匹配会大大增加成本。

对于给定的假定集合，特征点之间的邻域关系是固定的，因此可以预先计算出所有的成本值$\{c_i\}_{i=1}^N$。也就是说，方程中(13)唯一的未知变量是 pi ，其解很明显：任何与成本小于 λ 的对应将导致负项并减小目标函数，而任何与成本大于 λ 的对应将导致正项并增加目标函数目标函数。因此，最小化等式(13) 的 p 的最优解由以下简单标准确定：

$p_i= \begin{cases} 1,&c_i\leq\lambda\\ 0,&c_i>\lambda \end{cases} ,i=1,...,N\tag{15}$

因此，最优内点集$\mathcal{I}^*$由下式确定：

$\mathcal{I}^*=\{i|p_i=1,i=1,...,N\}\tag{16}$

从方程式（15），我们看到参数λ也起到了判断每个假定对应的匹配正确性的阈值的作用。请注意，当 ci = λ 时，pi 的设置可以是任意的。

3.3 邻域构建

方程 (3) 中每个点 x 的邻域 $\mathcal{N}_x$是基于整个特征集构建的，可能涉及异常值。由于以下原因，此策略效果很好。一方面，对于一个异常值（xi , yi ），它的局部邻域结构不能保留在两幅图像之间，导致成本 ci 很大，因此很容易被识别为异常值。另一方面，对于一个内点(x j , y j )，即使其邻域Nx j 或Ny j 包含一些异常值，主要成分是内点，这仍然符合几何约束。因此，它的成本c j 不会很大。

为了验证它的效果如何，我们总共收集了 30 个图像对，这些图像对具有不同类型的变换，包括分段线性变换、非刚性变形、宽基线图像对等

整个测试数据上 SIFT 匹配的平均初始内点百分比仅为 51.19%，因此异常点去除任务非常具有挑战性。使用精度和召回率作为我们评估匹配性能的指标，其中精度定义为识别出的正确匹配数与保留匹配数的比值，召回率定义为识别出的正确匹配数与假定集中包含的正确匹配数的比值。图 2 总结了关于不同 λ 的准确率和召回率曲线。我们看到，通过适当的 λ 值（例如，底行中的 0.9），我们的方法能够保留大约 84.58% 的真实匹配，并且精度也可以达到85.15%。此外，多尺度邻域表示的有效性也在图 2 中得到验证，其中上排和下排分别是未使用和使用多尺度邻域表示的结果。显然，多尺度邻域表示能够大大提高匹配性能。

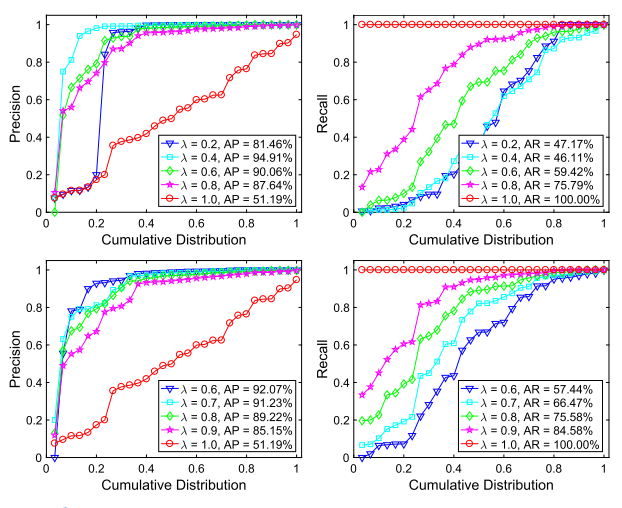
图2. 通过使用整个特征集构建邻域，对累积分布的精确度和召回率。顶行：不使用多尺度邻域表示的结果，例如，K = 6；底行：使用多尺度邻域表示的结果，例如，K = [4, 6, 8]。曲线上坐标为 (x, y) 的点表示有 100 * x 百分比的图像对具有不超过 y 的精度或召回率

然而，如果可以仅基于内点集$\mathcal{I}$构建邻域$\mathcal{N}_x$则更为可取。在这种情况下，内点的成本$c_j$的计算将更加准确，并且不受异常点的影响，因此，边际内点和异常点之间的距离会明显放大。这有助于推定对应关系的准确分类，尤其是当推定集合 S 包含大量异常值时。然而，真正的内点集是无法提前知道的，它需要在我们的问题中解决。

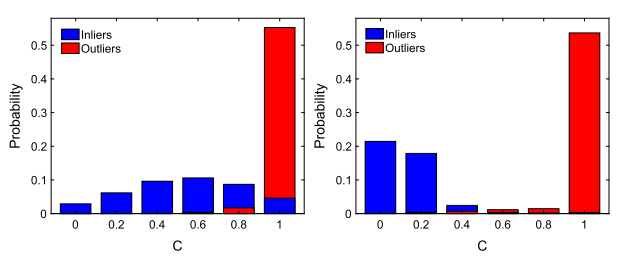
图3. 方程式 (14) 中成本 ci 的分布使用整个特征集（左）和使用 I0（右）构建邻域。对于每个 bin，我们将内部和异常概率重叠，其中概率较小的概率显示在外层

为了解决这个难题，我们在这里寻求它的近似值$\mathcal{I}_0$。如图 2 所示，我们的方法能够生成一个对应集，该对应集可以去除大部分异常值并同时保留大部分异常值，只需使用 S 进行邻域构建。显然，这个集合是真正的内点集合的一个很好的近似，即$\mathcal{I}_0=\arg\min_{\mathcal{I}}C(\mathcal{I};S,\lambda,\tau)$邻域是基于整个集合 S 构建的。

随后，我们使用$\mathcal{I}_0$为 S 中的每个对应关系构造邻域，并将最优$\mathcal{I}^*$求解为：

$\mathcal{I}^*=\arg\min_{\mathcal{I}}C(\mathcal{I};\mathcal{I}_0,S,\lambda,\tau)\tag{17}$

通过使用$\mathcal{I}_0$代替S进行邻域构建，30 个测试对的平均精确召回对可以从 (84.58%, 85.15%) 大幅提高到 (91.28%, 94.49%)。通过使用整个特征集和使用 I0 构建邻域的成本 ci 的分布如图 3 所示。我们看到内点和异常点之间的边距明显扩大。

实际上，我们可以使用渐进式策略来构建邻域，即迭代使用上一次迭代中生成的匹配集进行邻域构建直到收敛，然后将平均precision-recall对进一步提高到（92.26％，94.26％） ）。请注意，这种渐进策略只能稍微提高性能，这意味着 I0 足以逼近邻域构建的真实内点集。因此，我们只使用方程式(17) 为简单起见确定最优内点集。由于我们的匹配策略是保留局部邻域结构，我们将我们的方法命名为局部保留匹配 (LPM)。我们的 LPM 的整个过程已在算法 1 中进行了概述。

参数设置 我们的方法中有三个参数：K、λ 和 τ。参数 K 确定用于多尺度邻域构建的最近邻的数量。参数 λ 控制用于判断假定对应正确性的阈值。参数 τ 确定相邻假定匹配是否保留了邻域拓扑的一致性。显然，较大的 K 值、较小的 λ 值或较大的 τ 值将提高精度并同时降低召回率，反之亦然。在我们的评估中，我们根据经验将两次迭代中的默认值分别设置为 K = [4, 6, 8], τ = 0.2, λ = 0.9 和 0.5。

4 应用

本节描述了我们如何将局部保持匹配算法应用于几个不同的视觉任务，包括点集配准、视觉归巢和近重复图像检索，其性能通常由特征匹配质量决定。

4.1 非刚性点集配准

点集配准旨在确定正确的对应关系和/或恢复两组离散点之间的空间变换。配准问题通常通过使用迭代框架来解决，其中建立点对应关系来估计变换，反之亦然（Ma et al. 2017）。在这里，我们使用 LPM 算法在两个点集之间建立可靠的对应关系，并根据 Tikhonov 正则化（Micchelli 和 Pontil 2005）相应地估计变换。

4.1.1 一致建设

在配准问题中，点通常只是空间坐标并从形状轮廓中提取。因此，它们与 SIFT 等本地图像描述符无关。然而，在 2D 和 3D 情况下，有几个描述形状或点云的几何结构的描述符可用于建立假定的对应关系（Belongie et al. 2002; Rusuetal. 2009）。

对于 2D 情况，形状上下文 (SC)捕获相邻点的分布，已广泛用于形状匹配。考虑两个点$x_i和y_j$，它们的SCs是直方图$\{p_i(l)\}_{l=1}^L和\{q_j(l)\}_{l=1}^L$，L 是特征的维度。 χ2 距离用于测量它们的差异 D(xi , y j )：

$D(x_i,y_j)=\frac{1}{2}\sum_{k=1}^K\frac{[p_i(k)-q_j(k)]^2}{p_i(k)+q_j(k)}\tag{18}$

在计算了所有点对的距离，即$\{D(x_i,y_j)\}_{i,j=1}^{M_x,M_y}$之后，应用匈牙利方法 (Papadimitriou and Steiglitz 1982) 来寻找假定的对应关系两个点集。

对于 3D 情况，快速点特征直方图 (FPFH)可以用作特征描述符。它是表示底层表面模型属性的直方图，它收集每个点与其 k 最近邻点之间的成对平移、倾斜和偏航角，然后用相邻直方图对点的结果直方图进行重新加权。直方图的计算非常有效，它相对于表面法线的数量具有线性复杂性。 FPFH描述符的匹配是通过样本共识初始对齐方法进行的。

在使用一些局部特征描述符找到对应关系后，我们得到一个假定集合$S=\{(x_i,y_i)\}_{i=1}^N$。接下来，我们的 LPM 算法用于去除错误匹配并建立可靠的对应关系。

4.1.2 变换估计

转换$\mathbb{F}$，即$y_i=\mathbb{F}(x_i)$用于真实对应 (xi , yi )，可以通过刚性或非刚性模型来表征。刚性模型只涉及少量参数，相对容易，已被广泛研究。在这里，我们考虑更复杂和通用的非刚性模型，这是许多现实世界任务所必需的。要估计 f，自然会考虑回归等监督学习技术。

我们通过将变换$\mathbb{F}$限制在特定的函数空间$\mathcal{H}$内来对变换$\mathbb{F}$进行建模，即再现核希尔伯特空间 (RKHS) (Micchelli 和 Pontil 2005)，它由正定矩阵值核定义。在本文中，我们选择对角线可分解高斯核$\Gamma(x_i,x_j)=e^{-\beta\|x_i-x_j\|^2}\cdot\mathbb{I}$，其中 β 为扩展参数，$\mathbb{I}$为 2 × 2 单位矩阵。通过使用数据拟合的 L2 损失和模型复杂性的 L2 函数范数，Tikhonov 正则化最小化了以下正则化风险函数（Micchelli 和 Pontil 2005）：

$\varepsilon(\mathbb{f})=\min\{\sum_{i=1}^N\|y_i-\mathbb{f}(x_i)\|^2+\mu\|\mathbb{f}\|_{\mathcal{H}}^2\}\tag{19}$

根据代表定理（Micchelli and Pontil 2005），方程中的最小化问题的最优解由下式 (19) 给出：

$\mathbb{f}(x)=\sum_{i=1}^N\Gamma(x,x_i)w_i\tag{20}$

系数$\{w_i\}_{i=1}^N$由线性系统确定：

$(\Gamma+\mu I)W=Y\tag{21}$

其中$\Gamma\in\mathbb{R}^{N\times N}$是所谓的格拉姆矩阵$\Gamma_{ij}=e^{-\beta\|x_i-x_j\|^2}$，$W=(w_1,...,w_N)^T$和$Y=(y_1,...,y_N)^T$是$N\times 2$的矩阵

请注意，需要设置两个参数，即 μ 和 β，在本文中我们将它们固定为 μ = 3 和 β = 0.8。此外，为了使变换估计更加稳健，VFC (Ma et al. 2014) 算法更可取。它概括了 Tikhonov 正则化以在贝叶斯框架下处理受污染的数据，该框架引入了一个潜在变量来抵抗异常值。具体来说，它假设内点的噪声是高斯噪声，均值为零，标准差 σ 均匀，异常点是均匀分布的 1/a，a 是输入图像的面积。因此可能性是一个混合模型：

$p(X,Y|\theta)=\prod_{i=1}^N\bigg(\frac{\gamma}{2\pi \sigma^2}e^{-\frac{\|y_i,x_i-f(x_i)\|^2}{2\sigma^2}}+\frac{1-\gamma}{a}\bigg)\tag{22}$

其中$X=(x_1,...,x_N),\theta=\{\mathbb{f},\sigma^2,\gamma\}$包含一组待求解的未知参数，γ 为混合系数。通过在变换上施加一个缓慢而平滑的先验：$p(\mathbb{f}) ∝ e^{-\frac{\mu}{2}\|\mathbb{f}\|_{\mathcal{H}}^2}$，然后可以估计 θ 的 MAP 解，这通过使用迭代期望最大化方法来解决。特别是，在最大化步骤中，转换根据正则化风险函数更新为：

$\varepsilon(\mathbb{f})=\min\{\sum_{i=1}^Np_i\|y_i-\mathbb{f}(x_i)\|^2+\mu\sigma^2\|\mathbb{f}\|_{\mathcal{H}}^2\}\tag{23}$

其中 pi 是在期望步骤中估计的后验概率，它表示 (xi , yi ) 是内点的程度。我们参考 Ma 等人 (2014) 有关 VFC 算法的更多详细信息。

上述对应构造和变换估计两个步骤被迭代以获得可靠的结果。迭代次数固定为 10 次，如果输入数据劣化严重，则取值越大越好。

总结

1. LPM使用余弦相似度来判断邻域一致性，考虑到非刚性变换，使用阈值$\tau$来将余弦相似度二值化，依次提高非刚性变换时的适用性，但是使用这种方法会引入一定的误差，使得具有小误差的对应关系得以保留，使得F分数计算值偏低（我是用的F分数阈值是1.5，问题在于这个阈值是一定的吗，论文中使用的阈值是1.5吗？）
2. 旋转不变性：LPM使用的是余弦相似度，~~使用的是向量间的相对角度，~~通过设定阈值$\tau$来容忍向量间出现一定的夹角，使用邻域本身也具有一定的旋转不变性
3. 尺度不变性：通过改变K近邻的超参K来实现不同的尺度
4. 放射不变性：待定，没搞懂

补充内容

1. 余弦相似度

给定两个向量$A和B$，其余弦相似度表示为：

$similarity=\cos(\theta)=\frac{A\cdot B}{\|A\|\|B\|}=\frac{\sum_{i=1}^n A_i\times B_i}{\sqrt{\sum_{i=1}^n(A_i)^2}\times\sqrt{\sum_{i=1}^n}(B_i)^2}$

$F_{score}=$