NMRC：基于邻域流形表示一致性的鲁棒特征匹配

title

NMRC：基于邻域流形表示一致性的鲁棒特征匹配

Robust feature matching via neighborhood manifold representation consensus (sciencedirectassets.com)

摘要：

特征匹配旨在寻求两组特征之间的可靠对应关系，对于各种基于视觉的任务具有相当重要的意义。本文试图从基于描述符相似性创建的给定临时对应中消除错误对应。考虑到潜在真实匹配的稳定邻域拓扑，提出了一种简单而有效的方法，称为邻域流形表示一致性 (NMRC)，用于稳健的特征匹配。所提出方法的核心原理是在沿低维流形的潜在真实匹配中保留两个特征点之间的局部邻域结构。同时，为了提高数据严重劣化情况下的匹配性能，设计了一种基于邻域相似度的邻域构建迭代过滤策略。将匹配问题进一步公式化为基于邻域流形表示和迭代滤波策略的数学优化模型，推导出具有线性时间复杂度（即O(NlogN)）的闭式解，仅需几十毫秒处理超过 1000 个假定的通信。在一般特征匹配（大多数情况下 F-score > 94%）、遥感图像配准（大多数情况下 RMSE < 3）和回环检测方面的大量实验证明了所提出的方法在几个 state-of-the 上的显着优势- 艺术竞争对手，例如 RANSAC、MAGSAC++ 和 LPM。

1. 引言

识别两个特征集之间的可靠对应关系是摄影测量和计算机视觉中通常出现的基本问题（Ma et al., 2021; Li et al., 2020; Li et al., 2020）。这个问题是各种应用的关键先决条件，例如从运动中获取结构、SLAM、全景拼接以及图像和点集配准（Schonberger 和 Frahm，2016；Yu 等人，2021；Zhang 和 Ma , 2021)。由于其组合性质，匹配问题通常在计算上很复杂。具体来说，即使不考虑异常值，在 N 个点与另一个 N 个点之间建立一一对应关系也会产生 N!每个突变总数。解决上述挑战的一种流行策略是以两阶段模式解决匹配问题，即假定集生成和不匹配删除。在第一阶段，试验集通常是通过简单地整理出具有足够相似特征描述符的局部关键点对来生成的（例如，尺度不变特征变换，SIFT (Lowe, 2004)）。然而，除了真正的对应（即内点）之外，假定的集合通常被大量的错误对应（即异常值）所污染。这种污染归因于局部特征表示的模糊性（尤其是当图像质量低劣、重复结构或遮挡时）。因此，在下一步中设计一种稳健的方法来过滤错误的对应关系以增强它们的可靠性是必不可少的。

许多现有的方法通常通过施加几何约束（例如，运动平滑约束）来消除错误的对应关系，这会限制对应关系以满足基础几何模型。因此，有必要提前定义一个变换模型，它可以是参数的（例如仿射、单应性和对极几何）或非参数的（例如非刚性）。然而，基于参数模型的方法很容易由于未知的变换模型或发生非刚性变形而失败。

此外，现有方法的另一个缺点是非刚性变换模型的计算复杂度高。最近有几种技术研究了内点的局部一致假设以进行错配消除（Ma et al., 2019; Bian et al., 2020; Li et al., 2019）。这些方法中的几何约束被放宽，然后通过简单而有效的规则过滤异常值。即使在运动不连续的场景中，这些方法也可以实现良好的性能。但是，由于在这些技术中忽略了输入数据的基本内在几何形状，因此也保留了一些总异常值。

为了解决上述挑战，本文引入了一种称为邻域流形表示共识（NMRC）的稳健且有效的方法，用于稳健的特征匹配。对于相似对象或场景的一对图像，表征局部拓扑的特征点之间的空间邻域关系通常是稳定的，并且尽管图像旋转、缩放或非刚性变换，但由于物理约束可能不会倾向于自由变化（Ma et等人，2015）。因此，通过流形学习设计了特征点邻域的数学表示，类似于局部线性嵌入 (LLE) (Roweis and Saul, 2000)，并引入了数学优化模型。该模型根据邻域流形表示的相似性去除异常值。该公式是稳健的，不需要预定义的转换模型。进一步推导了具有线性时间复杂度和线性空间复杂度的简单闭式解。此外，设计了一种迭代过滤策略，为优化模型中的邻域流形表示提供一组相对干净的匹配。对用于一般特征匹配的各种真实数据和遥感图像配准和回环检测等两个真实世界任务的实验表明，与几种最先进的替代方案相比，NMRC 可以实现更令人满意的性能。

本文的贡献包括以下三个方面：

  • 为特征匹配提出了邻域流形表示共识。与需要预定义全局图像转换的无数现有方法相比，所提出的方法仅试图使用流形学习来保持局部对潜在内点的拓扑的共识。因此，所提出的方法对复杂的图像变换具有鲁棒性。
  • 为邻域构建设计了一种迭代过滤策略，可确保邻域流形表示不会受到总异常值的影响。
  • 引入了一种鲁棒的数学优化模型，并推导了它的闭式解，具有线性时间复杂度，有利于许多实时应用。任何用于表征真实匹配和不匹配之间潜在差异的度量都可以集成到基于该模型的公式中。

本文的其余部分安排如下。第 2 节描述了背景材料和相关工作。第 3 节提供了用于稳健特征匹配的 NMRC 算法的详细信息。第 4 节说明了该方法与其他方法在不同类型的实际应用中的实验结果。第 5 节最后给出了结论。

2. 相关工作

特征匹配已广泛应用于计算机视觉、摄影测量、遥感和机器人等各个领域。 （Ma 等人，2021 年；Zitova 和 Flusser，2003 年；Jiang 等人，2021 年）中总结了一些关于该任务的代表性评论。上述文献表明，现有的特征匹配方法大致可分为以下三类：基于双步策略、基于对应矩阵和基于学习的方法。

2.1 基于两步策略的方法

在计算机视觉领域，具有基于几何约束的方法的特征描述符通常将特征匹配转换为两步方式（Ma et al., 2014）：建立假定匹配，然后使用几何约束过滤错误匹配。推定集通常是通过修剪所有可能的点对应的集合来获得的。这个场景是通过计算点上特征描述符的相似度并去除描述符过度不同的对应关系来实现的。具有代表性的是，SIFT (Lowe, 2004) 将最近邻和次近邻之间的距离比与预定义的阈值进行比较，以消除不稳定的匹配，表现出令人满意的性能。湾等人。 (2006) 引入了 Haar 小波计算来近似梯度计算并进一步加速 SIFT 算子。此外，积分图像策略用于简化 Haar 小波响应的计算，使其性能比 SIFT 更有效。值得注意的是，ORB (Rublee et al., 2011) 是目前建立假定匹配的最快方法之一。此外，当两个待匹配点的集合具有物理形状时，形状上下文 (SC) (Belongie et al., 2002) 可用于构造描述符。尽管有各种精心设计的假定匹配生成方法，但由于局部描述符的模糊性，假定的集合不可避免地受到大量不匹配的污染。因此，下一步需要通过几何约束来确定和消除不匹配，从而产生有希望的匹配性能。为此，过去几十年出现了各种方法，大致可分为以下四类：统计回归、重采样、非参数拟合和图匹配方法。

统计领域有大量关于稳健估计的文献（Rousseeuw 和 Leroy，2005；Huber，1981）。研究表明，与二次 L2 范数相比，最小化 L1 范数是更好的选择，因为它具有更强的鲁棒性和容忍相当大比例的异常值的能力。最小中值平方 (LMedS) (Rousseeuw and Leroy, 2005) 和 M 估计量 (Huber, 1981) 是稳健的估计量。 LMedS 可以处理很大比例的异常值，但效率较低，而 M 估计器需要对模型参数进行良好的初始化。迈尔等人。 （2016）最近提出了一种基于统计光流的引导匹配策略，考虑到准确性和效率，该策略具有良好的性能。重采样方法无疑是这项任务最流行的范例。这些方法遵循假设和验证策略，旨在找到最小可能的无异常值子集以拟合预定义的参数模型。特别是随机样本共识 (RANSAC) (Fischler and Bolles, 1981) 及其变体（例如 MLESAC (Torr and Zisserman, 2000)、GESAC (Li et al., 2020) 和 MAGSAC++ (Barath et al., 2021) ) 是这种类型的代表。

尽管结果令人满意，但统计回归和重采样方法也有一些局限性。一方面，这些方法依赖于几何参数模型，无法在复杂的变换下工作。另一方面，这些方法在存在大量异常值的情况下容易出现严重退化（Li and Hu，2010）。最近提出了许多非参数拟合方法来解决上述挑战（Ma et al., 2014; Li and Hu, 2010）。这些方法用先验条件插入一个非参数函数，其中特征对应的运动是缓慢而平滑的。然而，在场景中存在深度不连续或独立运动的情况下，先验条件并不总是正确的。此外，这些方法通常具有很高的计算复杂性，这限制了它们对实时任务的适用性。图模型提供了另一种处理特征匹配问题的观点。包括光谱匹配（Leordenu 和 Hebert，2005 年）、模式搜索（Wang 等人，2014 年）和图位移（GS）（Liu 和 Yan，2010 年）在内的一些代表性研究是可用的。值得注意的是，图匹配的转换模型相当灵活。然而，这个模型也有类似的缺点，即它的非多项式难性质。

然而，这个模型也有类似的缺点，即它的非多项式难性质。除了之前提到的重采样等方法外，最近还研究了许多松弛方法。此类方法通过假设局部结构一致性或分段平滑约束来执行正确匹配的稳健估计。例如，局部保持匹配 (LPM) (Ma et al., 2019) 试图保持潜在真实匹配的局部邻域结构。局部结构一致性约束 (LSCC) (Shao et al., 2020) 使用新的局部结构描述符评估每个对应关系以消除不匹配。基于网格的运动统计 (GMS) (Bian et al., 2020) 将平滑度约束封装为区域中一定数量对应关系的统计似然性，并利用基于网格的方案来加速计算。最小相对运动熵 (MRME) (Shao et al., 2021) 将特征匹配问题转化为局部相对运动一致性估计，为此制定了相对线性运动和相对角运动。

2.2 基于对应矩阵的方法

特征匹配的另一种策略是将两个特征集的对应矩阵与参数或非参数几何约束集成，其中匹配问题也称为纯点集匹配问题，即局部关键点通常没有信息特征描述符。具有代表性的是，迭代最近点 (ICP) (Besl and McKay, 1992) 利用最近点策略交替分配二进制对应关系。之后，ICP通过估计的对应关系执行封闭形式的刚性变换估计，直到收敛。 Chui 和 Rangarajan (2003) 介绍了一种基于薄板样条 (TPS) 的非刚性匹配通用框架。杨等人。 （2015）进一步提出了一种方法，即全局和局部混合距离（GLMD），以增强对数据退化的鲁棒性；这种方法取得了良好的效果。近年来出现了许多基于概率的点集配准方法。例如，Myronenko 和 Song (2010) 提出了著名的基于高斯径向基函数的相干点漂移 (CPD) 方法，随后引入了许多变体 (Ma et al., 2016; Sun et al., 2016)。 , 2020a)。这些方法将匹配问题转化为使用高斯混合模型 (GMM) 估计混合密度，这些模型在概率框架和 EM 算法中得到解决。

基于对应矩阵的方法在刚性和非刚性场景下都能取得很好的效果。但是，这些方法可能会由于异常值过多或数据严重退化而失败。此外，该框架是一个复杂的组合优化问题，具有复杂的解空间，在迭代估计过程中需要大量的时间消耗。

2.3 基于学习的方法

近年来，深度学习方法由于其学习和表达能力越来越多地应用于计算机视觉的各个领域，并在图像匹配任务中取得了显着进展。深度学习方法通常用于直接从包含相同或相似场景的图像对中学习像素级匹配关系。具体而言，当前文献中流行以下三种管道：

  • 学习取代传统基于特征的方法的一个或多个过程或直接设计端到端匹配网络；例如，学习从图像中检测出一组准确可靠的特征点，学习每个特征点的主要方向或尺度及其更具区分性和匹配性的特征描述符，例如 LIFT (Yi et al., 2016) 和 SuperPoint （DeTone 等人，2018 年）。但是，如果异常值比比皆是，仍然需要使用不匹配删除策略进行后处理。

  • 训练卷积神经网络 (CNN) 通过估计两个图像的相似性度量来驱动迭代优化策略 (Simonovsky et al., 2016)。

  • 通过 CNN 回归器直接估计变换参数。具有代表性的是，学习找到好的对应关系 (LFGC) (Moo Yi et al., 2018) 是作为消除错配的第一次尝试而开发的。给定一个假定的集合和相机内在函数，LFGC 尝试训练一个基于多层感知器的深度网络，以将对应关系标记为内点或异常点，并同时恢复相对姿势。然而，LFGC 需要已知的相机内在函数作为输入和特定的参数模型，严重限制了其在实际应用中的价值。此外，LFGC 还推动了多项后续工作，例如 OA-Net (Zhang et al., 2019) 和 ACNe (Sun et al., 2020b)。此外，SuperGlue (Sarlin et al., 2020) 是另一个新颖的想法，最近有人提出用图神经网络从局部特征生成可靠匹配。尽管如此，这个想法仍然表明输出中存在大量不匹配。创新地，Ma 等人（2019）将该问题表述为一个二分类问题。这样的公式使该方法能够在数据尺度上实现具有线性时间复杂度的有希望的匹配性能，但由于其匹配表示缺陷，可能会保留一些粗略的异常值。最近，陈等人（2021）引入了一种称为局部结构可视化-注意力网络（LSV-ANet）的深度学习网络，旨在将不匹配消除转化为动态视觉相似度评估，并取得良好的性能。然而，这种想法对特征点周围小区域中存在的异常值很敏感，这限制了 LSV-ANet 识别细粒度模式的能力及其对复杂匹配场景的泛化能力。

3. 方法实现

本节提供了所提出的鲁棒特征匹配方法NMRC的详细信息。不失一般性，从两个给定图像中提取一组 N 个假定匹配S={(xi,yi)}i=1NS=\{(x_i,y_i)\}_{i=1}^N，其中 xi 和 yi 是二维列向量，分别表示来自两个不同图像的特征点的空间位置。以下讨论集中在通过邻域流形表示一致从 S 中消除不匹配。

3.1 动机

下图表明特征点的邻域拓扑结构通常是稳定的，在不同的图像变换下略有变化。因此，在处理失配消除问题时，利用特征点的邻域结构信息是必不可少的。为此，在提出问题公式之前，首先考虑了一种鲁棒的邻域流形表示策略来处理两个图像之间的特征对应关系。

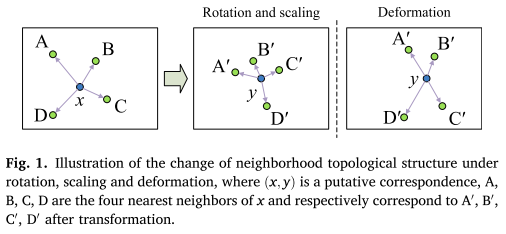
图1. 邻域拓扑结构在旋转、缩放和变形下的变化示意图，其中（x，y）是假定的对应关系，A，B，C，D是x的四个最近邻，分别对应于转化后的A′，B′、C’、D’。

3.1.1 邻域流形表示

邻域流形表示通常不仅应捕获邻域结构信息，还应证明鲁棒性，以适应各种图像变换。为了实现这一目标，我们设计了一种类似于经典LLE算法（Roweis和Saul，2000）的有效策略，该算法是一种非线性降维方法，用于在低维流形中保持局部邻域结构。

特别是，首先在X={xi}i=1N\mathcal{X}=\{x_i\}_{i=1}^N中搜索每个特征点xi的K近邻，并将其视为欧几里得距离下的邻域NxiK\mathcal{N}_{x_i}^K。假设WkW^k是N × N权重矩阵，如果xjx_j不属于xix_i的邻居，则强制WijxW_{ij}^x = 0。第二，通过以下成本函数测量的重建误差被最小化:

In this approach, we start by searching for the K-nearest neighbors of each feature point xi in the set X={xi}i=1N\mathcal{X}=\{ x_i\}_{i=1}^N and treating them as the neighborhood N∗xiK\mathcal{N}*{x_i}^K defined by Euclidean distance. We then construct an N × N weight matrix WkW^k, where WijxW_{ij}^x is set to 0 if xjx_j is not a neighbor of xix_i. Finally, we minimize the reconstruction error measured by the following cost function

ε(Wx)=∑i=1N∥xi−∑j=1NWijxxj∥2(1)\varepsilon(W^x)=\sum_{i=1}^N\Vert x_i-\sum_{j=1}^N W_{ij}^x x_j\Vert^2\tag{1}

这种最小化是在重构权重矩阵的行总和为 1 的约束下执行的：∀i,∑i=1NWijx=1\forall i,\sum_{i=1}^N W_{ij}^x=1。最优权重WijxW_{ij}^x可以通过求解最小二乘问题得到。第三，通过仅保留WxW^x每行中的非零元素，将WxW^x替换为N×KN\times K矩阵WxW^x。可以通过使用权重矩阵WxW^x进行邻域表示来实现在旋转，缩放和局部分解下对邻居拓扑结构变化的鲁棒性。

接下来，本研究着重于Y={yi}i=1N\mathcal{Y}=\{y_i\}_{i=1}^N中每个yiy_i的邻域表示的构建。为此，{NxiK}i=1N\{\mathcal{N}_{x_i}^K\}_{i=1}^N被用于标识集合{CyiK}i=1N\{\mathcal{C}_{y_i}^K\}_{i=1}^N，每个元素表示NxiK\mathcal{N}_{x_i}^K在Y\mathcal{Y}中对应的特征点，如下图所示。

获取集合{CyiK}i=1N\{\mathcal{C}_{y_i}^K\}_{i=1}^N后，将其与式（1）相结合，然后使用CyiK\mathcal{C}_{y_i}^K重构每个特征点yiy_i。因此，获得了N×KN\times K权重矩阵WyW^y。 WxW^x和WyW^y的第 i 行分别表示特征点 xi 和 yi 的邻域拓扑信息，可以表征为:

Wix=(Wi1x,...,wiKx)∈R1×KWiy=(Wi1y,...,wiKy)∈R1×K(2)W_i^x=(W_{i1}^x,...,w_{iK}^x)\in \mathbb{R}^{1\times K}\\ W_i^y=(W_{i1}^y,...,w_{iK}^y)\in \mathbb{R}^{1\times K}\tag{2}

具体来说，WixW_i^x和WiyW_i^y是$ 1 \times K 权重向量，分别包含权重向量，分别包含\mathcal{N}{x_i}K$和$\mathcal{C}_{y_i}K的重建权重。例如，的重建权重。例如，W{iK}x$表示$\mathcal{N}_{x_i}K中第K个邻居的权重，以重建中第 K 个邻居的权重，以重建x_i$。

如前所述，正确的匹配应该在两幅图像之间具有稳定的局部邻域结构。因此，邻域结构信息表示为WixW_i^x和WiyW_i^y对于正确的匹配（xi，yix_i，y_i）应相似的，如图2（a）所示。为此，定义了一个距离度量来描述（xi，yix_i，y_i）邻域拓扑的差异，如下所示：

DistK(xi,yi)=∥Wix−Wiy∥2(3)Dist_K(x_i,y_i)=\Vert W_i^x-W_i^y\Vert^2\tag{3}

直观地，当等式中的距离较小时，当在等式(3)中的距离接近于 0时，匹配的特征点（xi，yix_i，y_i）之间的邻域拓扑差异很小,因此使其成为内点，反之亦然。

对于假定的匹配（xi，yix_i，y_i），如果NxiK\mathcal{N}_{x_i}^K和CyiK\mathcal{C}_{y_i}^K是由内点构造的，则上述方案提供了内点或离群点的满意指示。

pic2

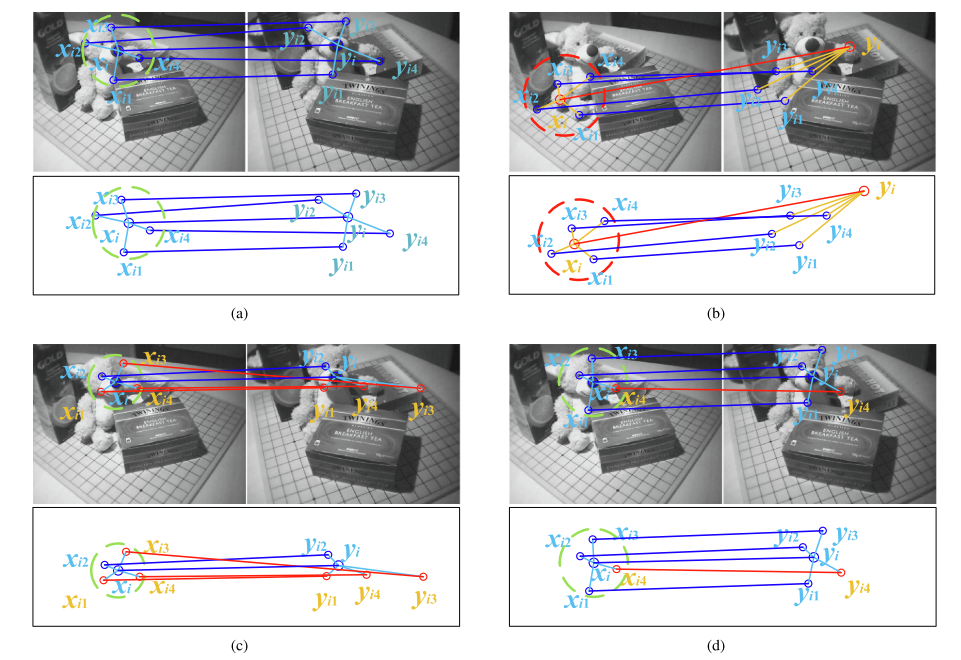
图2. 邻域重建共识测量的插图。我们搜索特征点 xi 的 K 个最近邻（K = 4），然后获取包含 xi1、xi2、xi3、xi4 的 NxiK\mathcal{N}_{x_i}^K。接下来，NxiK\mathcal{N}_{x_i}^K用于识别由 yi1、yi2、yi3、yi4 组成的CyiK\mathcal{C}_{y_i}^K，分别对应于 xi1、xi2、xi3、xi4。NxiK\mathcal{N}_{x_i}^K和CyiK\mathcal{C}_{y_i}^K仅在前两种情况下包含内点，在后两种情况下包含外点。由方程式(3) 表征的距离四种情况分别为 0.012、30.11、27.55 和 0.109。 蓝色：真匹配； 红色：错误匹配。

如图2（a）和（b）所示，对于具有较大裕度的内部值和异常值，DistK(xi,yi)Dist_K(x_i,y_i)分别为0.012和30.11。然而，内点无法预先知道，当图像发生复杂变形时，NxiK\mathcal{N}_{x_i}^K和CyiK\mathcal{C}_{y_i}^K将不可避免地受到异常值的污染，导致性能退化。如图 2© 所示，（xi，yix_i，y_i）是一个内点，但DistK(xi,yi)Dist_K(x_i,y_i)的值很大，为 27.55。因此，确保NxiK\mathcal{N}_{x_i}^K和CyiK\mathcal{C}_{y_i}^K包含尽可能少的异常值对于提高匹配性能至关重要。如图2（d）所示，NxiK\mathcal{N}_{x_i}^K和CyiK\mathcal{C}_{y_i}^K有一定程度的改善（仍包含异常值），然后DistK(xi,yi)Dist_K(x_i,y_i)急剧下降至0.109。下面介绍一种迭代过滤策略，以实现上述目标，并尽可能多地清理邻居NxiK\mathcal{N}_{x_i}^K和CyiK\mathcal{C}_{y_i}^K。

3.1.2 邻域构造的迭代滤波

如上所述，邻里应该足够干净，以确保DistK的可分辨性。因此，用于邻域构造的对应应包含一些异常值，同时保留大多数内点值。对于假定集S中的内点对（xi，yix_i，y_i），xi和yi的邻域应该相似，并且包含许多公共元素。相反，异常值（xi，yix_i，y_i）的xi和yi的邻域应该非常不同，并且不包含公共元素。该特性称为邻域相似性，如图3所示。

图3. 邻域相似性示意图。对于正确的匹配 (xi, yi)，Nxi\mathcal{N}_{x_i}应该有很多与Nyi\mathcal{N}_{y_i}相同的元素.对于一个错误的匹配(xj,yj)，Nxj\mathcal{N}_{x_j}应该与Nyj\mathcal{N}_{y_j}几乎没有共同点。蓝线和红线分别代表内点和异常点。

因此，假设邻域的尺度为κ，NxiK\mathcal{N}_{x_i}^K和NyiK\mathcal{N}_{y_i}^K之间的邻域相似度可以表示为如下所示，以从数学上捕捉该特性：

Ratio(i)=ni/k(4)Ratio(i)=n_i/k\tag{4}

其中ni=∣NxiK∩NyiK∣≤kn_i=\mid\mathcal{N}_{x_i}^K \cap \mathcal{N}_{y_i}^K\mid\leq k是两个邻域NxiK\mathcal{N}_{x_i}^K和NyiK\mathcal{N}_{y_i}^K中公共元素的数量，且Ratio(i)∈[0,1]Ratio(i)\in[0,1]，这是对应邻域中公共特征点的比率。由内点引起的比率值将很大，反之亦然。然而，即使（xi，yix_i，y_i）是一个内点，Ratio(i) 也可能很小，因为 S 可能包含相当数量的异常值，并且当 κ 很大时，Ratio(i) 的可区分性会同时变弱。

引入迭代过滤策略来解决这个问题。 特别地，使用一组阈值{ηm}m=1M\{\eta_m\}_{m=1}^M，并且逐步过滤不满足Ratio > ηm的不可靠匹配。可靠集Um\mathcal{U}_m包括预先提供的匹配：

Um={(xi,yi)∈S∣Ratio(i)>ηm, i=1,...,N}(5)\mathcal{U}_m=\{(x_i,y_i)\in S|Ratio(i)>\eta_m,\ i=1,...,N\}\tag{5}

其中，**Um\mathcal{U}_m表示第 m 次迭代后的可靠集，且ηm\eta_m表示第 m 次迭代的阈值。**尤其地，使用Um−1来构造{NxiK}i=1N\mathcal{U}_{m-1}来构造\{\mathcal{N}_{x_i}^K\}_{i=1}^N和{NyiK}i=1N\{\mathcal{N}_{y_i}^K\}_{i=1}^N，当Um\mathcal{U}_m由等式4、5获得时，且U0\mathcal{U}_0被定义为S。可靠集合也是基于整个集合 S 而不是Um−1\mathcal{U}_{m-1}。此外，初始阈值η1\eta_1设置为一个小值。因此，U1包含足够的对应关系，以便在下一次迭代中构建邻域。通过使用该迭代滤波策略，在公式（3）中的距离度量计算期间，最终可靠集Um\mathcal{U}_m通常对于邻域构造足够干净。

3.2 问题表述

在本节中，基于所提出的鲁棒邻域流形表示，将不匹配消除问题转化为数学优化模型。特别是，保持特征点局部拓扑的最佳解决方案是:（？）

I∗=arg⁡minIC(I;S,UM,λ)(6)\mathcal{I}^*=\arg min_{\mathcal{I}}C(\mathcal{I};S,\mathcal{U}_M,\lambda)\tag{6}

C表示成本函数，定义为：

C(I;S,UM,λ)=∑i∈IDistK(xi,yi)+λ(N−∣I∣)(7)C(\mathcal{I};S,\mathcal{U}_M,\lambda)=\sum_{i\in \mathcal{I}}Dist_K(x_i,y_i)+\lambda(N-|\mathcal{I}|)\tag{7}

其中，式（3）中定义的DistK(xi,yi)Dist_K(x_i,y_i)衡量xi和yi之间相邻流形表示的一致性，可靠集Um\mathcal{U}_m用于构造NxiK\mathcal{N}_{x_i}^K和CyiK\mathcal{C}_{y_i}^K，并且∣⋅∣|·|是集合的基数。内点集合I\mathcal{I}表示选取∣⋅∣|·|对点，使得尽可能选取最多的点且这些点对的度量距离尽可能小。

此成本函数中的第一项惩罚任何不保留邻域流形表示的共识的对应关系，第二项用于阻止不匹配，参数 λ> 0用于平衡这两个项。最优解应该理想地实现零惩罚，即 C 的第一项应该为零。该解决方案试图在获取最大内点集的同时最小化成本函数的值。值得注意的是，方程 (6)中的目标函数是平移、旋转和缩放不变的。然后可以通过最小化等式 (6)来解决消除不匹配的问题。

引入 N×1 二元向量 p 以优化目标函数 (6) 并表征假定对应关系的正确性，即pi=1p_i=1表示内部值，0 表示异常值。因此，方程式 (7) 可写为：

C(p;S,UM,λ)=∑i=1NpiDistK(xi,yi)+λ(N−∑i=1Npi)(8)C(p;S,\mathcal{U}_M,\lambda)=\sum_{i=1}^N p_i Dist_K(x_i,y_i)+\lambda(N-\sum_{i=1}^N p_i)\tag{8}

然后通过合并与pip_i相关的术语来重组其形式，并获得：

C(p;S,UM,λ)=∑i=1Npi(ci−λ)+λN(9)C(p;S,\mathcal{U}_M,\lambda)=\sum_{i=1}^N p_i(c_i-\lambda)+\lambda N\tag{9}

其中，

ci=DistK(xi,yi)(10)c_i=Dist_K(x_i,y_i)\tag{10}

衡量第i个对应（xi，yix_i，y_i）是否满足保持邻域重建一致性的几何约束。一个内点将产生零或小成本，而一个外点将导致大成本。

3.3 封闭形式的解决方案

给定一个暂定集 S，特征点之间的局部拓扑是固定的。因此，{ci}i=1N\{\mathcal{c}_i\}_{i=1}^N可以被预先估计。

方程式(9)中唯一的未知变量是pip_i。pip_i值的估计表明，任何假设的匹配成本小于 λ 都会导致负项并降低目标函数。因此，最好将pip_i的值设置为 1，反之亦然。具体来说，最小化等式(9) 的 p 的最优解可以通过以下简单标准确定：

pi={1,if ci<λ0,if ci>λ, i=1,2,...,N(11)p_i= \begin{cases} 1,&if\ c_i<\lambda\\ 0,&if\ c_i>\lambda \end{cases} ,\ i=1,2,...,N\tag{11}

因此，最优内点集I∗\mathcal{I}^*可以表示为：

I∗={i∣pi=1,i=1,2,...,N}(12)\mathcal{I}^*=\{i|p_i=1,i=1,2,...,N\}\tag{12}

参数 λ 作为阈值来确定假定集合的正确性。同时，由于采用了迭代过滤策略，邻域Nx\mathcal{N}_x是在可靠集 UM\mathcal{U}_M的基础上构建的。因此，DistK(xi,yi)Dist_K(x_i,y_i)的值是两个对应特征点 xi 和 yi 之间局部拓扑一致性的准确指示。

上述配方可以产生令人满意的结果。但是，基于理想的内点集I\mathcal{I}构造局部邻域{NxiK}i=1N\{\mathcal{N}_{x_i}^K\}_{i=1}^N将进一步提高异常值的去除性能，尤其是当假定的集S充满异常值时。

由方程 (12)得到的匹配集的匹配精度远高于 UM\mathcal{U}_M。因此，在得到基于等式(12)的内点集I0\mathcal{I}_0之后，即I0=arg⁡minIC(I;S,UM,λ)\mathcal{I}_0=\arg min_{\mathcal{I}}C(\mathcal{I};S,\mathcal{U}_M,\lambda)，我们用它来代替 UM\mathcal{U}_M进行邻域构建。 最后得到最优内点集I*如下：

I∗=arg⁡minIC(I;S,I0,λ)(13)\mathcal{I}^*=\arg min_{\mathcal{I}}C(\mathcal{I};S,\mathcal{I}_0,\lambda)\tag{13}

值得注意的是，上述过程可以迭代以进一步提高匹配性能，即迭代使用前一次迭代中生成的对应集进行邻域构建，直到收敛。

但是，这样的迭代只能稍微提高匹配性能，这表明I0\mathcal{I}_0足够好，可以近似于邻域构造的真实内列集。因此，只有等式(13) 用于确定最优内列集I∗\mathcal{I}^*。

提出的方法侧重于保持邻域流形表示的共识。因此，这种方法被命名为NMRC，整个过程在Alg1中进行了总结。

3.4 讨论

值得注意的是，尽管所提出的方法与 LPM 的工作具有相似的公式（Ma et al., 2019），但它们之间存在显着差异。首先，LPM 仅利用其在假定集合 S 中的 K 个最近邻来构造特征点 x 的邻域，即假定集合 S 用于构造{NxiK}i=1N\{\mathcal{N}_{x_i}^K\}_{i=1}^N。当 S 包含大量异常值时，邻域将不可避免地被异常值污染，导致 LPM 性能退化。相比之下，所提出的方法利用基于邻域相似性的迭代过滤策略来构建邻域，即使用可靠集UM来构造{NxiK}i=1N\{\mathcal{N}_{x_i}^K\}_{i=1}^N，这可以提高匹配性能。

其次，LPM中两个特征点之间的邻域结构相似度只考虑了K-NN的简单运动统计，不能利用真实的局部结构。换句话说，LPM 中的测量标准不够严格，无法保留邻域拓扑结构。然而，所提出的方法通过利用流形学习充分利用特征对应的潜在内在几何信息，为邻域拓扑结构保存引入了更严格的约束。简而言之，所提出的方法能够更严格地保持邻域拓扑一致性，并具有更鲁棒和准确的匹配性能。这将在后续的实验结果中得到验证。

3.5 计算复杂度

给定包含N个对应关系的推定集合S，通过使用K-D树 (Bentley，1975)，为S中的每个对应关系搜索K个最近邻的时间复杂度接近$ O((K + N) log N)。因此，算法1中第2−6行和第8行的时间复杂度分别约为。因此，算法1中第2-6行和第8行的时间复杂度分别约为O(M(k+N)\log N)和和O((K+N)\log N)，计算第9行和第12行的代价，计算第9行和第12行的代价{c_i}_{i=1}^N需要得到重构权重矩阵W，根据公式(1)，其中具有需要得到重构权重矩阵W，根据公式 (1)，其中具有O(K3N)$时间复杂度，因为W的每行可以用$O(K3)时间复杂度分别求解。考虑到第11行和第8行时间复杂度的相似性，建议的NMRC的总时间复杂度约为时间复杂度分别求解。考虑到第11行和第8行时间复杂度的相似性，建议的NMRC的总时间复杂度约为O((Mk+MN+K+N)\log N+K^3N)。考虑到存储邻域的内存，NMRC的空间复杂度为。考虑到存储邻域的内存，NMRC的空间复杂度为O((k+K)N)。M、K和κ通常远小于N。因此，该方法的时间和空间复杂性可以简单地分别写为。M、K和 κ 通常远小于N。因此，该方法的时间和空间复杂性可以简单地分别写为O(NlogN) 和和O(N)$。因此，NMRC在给定暂定集的规模方面具有线性时间和线性空间复杂性。因此，所提出的方法适用于处理现实世界的任务。

3.6 实施细节

必须为 NMRC 设置几个参数：K,k,{ηm}m=1M,M,λK,k,\{\eta_m\}_{m=1}^M,M,\lambda

参数 K 表示基于流形学习的邻域表示的最近邻数。参数 κ 控制迭代过滤策略中邻域构造的大小。参数ηm是一个阈值，用于判断一个对应关系是否属于可靠集。参数 M 决定了迭代过滤策略的迭代次数。参数 λ 作为区分假定匹配正确性的阈值。较大的 M、ηm 和 κ 值通常会提高可靠对应集的质量，但同时会牺牲一部分真实匹配。 较大的 K 值和较小的 λ 值将提高精度，同时降低召回率，反之亦然。

实验评估中的默认值设置为K = 10, κ = 10, ηm = [0.2, 0.5, 0.5],M = 3, and λ = [0.12, 0.12]。

4. 实验结果

在本节中进行所提出的 NMRC 的消融实验，然后评估真实图像对的特征匹配性能。随后，测试了 NMRC 的鲁棒性，最终将该方法应用于解决两个现实世界的任务，即图像配准和回环检测。开源 VLFEAT 用于使用 K-D 树搜索 K-最近邻（Vedaldi 和 Ful kerson，2010）。所有实验均在配备 2.4 GHz Intel Core i5-6200U CPU、8 GB 内存和 MATLAB 代码的台式机上进行。

4.1 消融研究

选择了 30 对包含刚性、旋转、尺度变化和非刚性变形等不同变换的真实图像对进行评估，以验证所提方法的有效性。 SIFT 在整个测试数据上获得的假定对应的平均初始内点百分比约为 57.02%，这使得错配去除任务具有挑战性。采用精确率和召回率来表征性能；精度定义为已识别的内点数与保留的匹配数的比值，召回率是已识别的内点数与整个内点数的比值。

首先，研究了 ηm、κ、K 和 λ 的最佳参数设置。因此，在 30 个测试图像对上针对 ηm 的不同参数设置测试了平均 F 分数，结果如图 4 所示。特别是，{η1, η2, η3} 的一个参数固定为其“最优”参数设置，并改变其他两个参数以确定最优阈值集合{ηm}m=1M\{\eta_m \}_{m=1}^M。

pic4

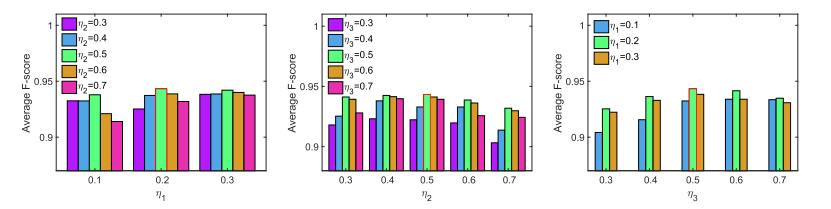
结果表明，ηm = [0.2, 0.5, 0.5] 实现了最佳的平均 F-score，在本文中被视为默认的最优 ηm。还在 30 个测试图像对上测试了不同的设置，以确定 κ、K 和 M 的最佳值，并且平均 F 分数和运行时间总结在表 1-3 中。

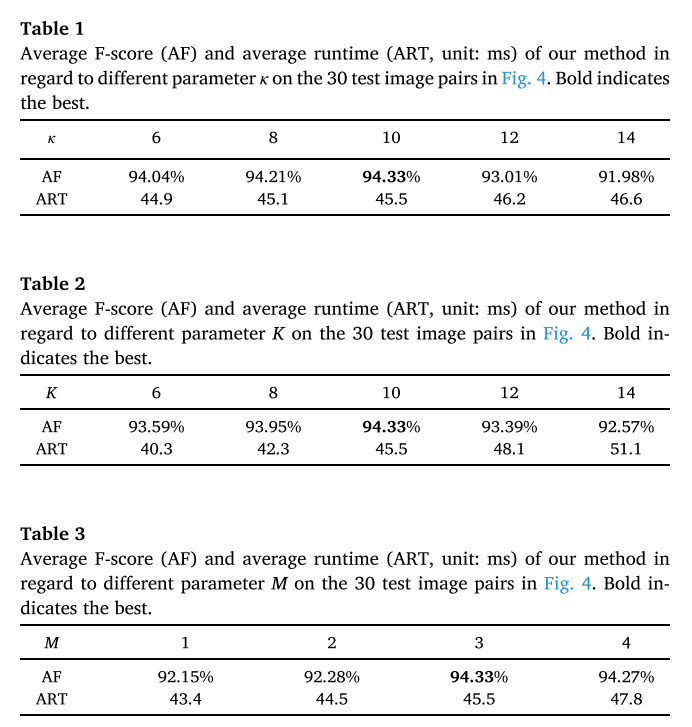
table1-3

结果表明 κ = 10、K = 10 和 M = 3 被认为是它们的默认最优设置，可以达到最佳性能。考虑到参数 λ 的强烈影响，使用不同的 λ 对从选定的测试图像对中分类的各种图像变换测试平均 F 分数，结果如图 5 所示。这些结果表明考虑到各种类型的图像变换，λ 的最佳选择可能会略有变化。因此，λ = 0.12 被设置为其默认的最佳设置，因为它在所有数据上的平均 F 分数最好。请注意，通过使用网格搜索方法可以更准确地确定最佳参数。然而，所提出的方法中的大量参数（例如，超过 6 个）使得难以使用网格搜索。

pic5

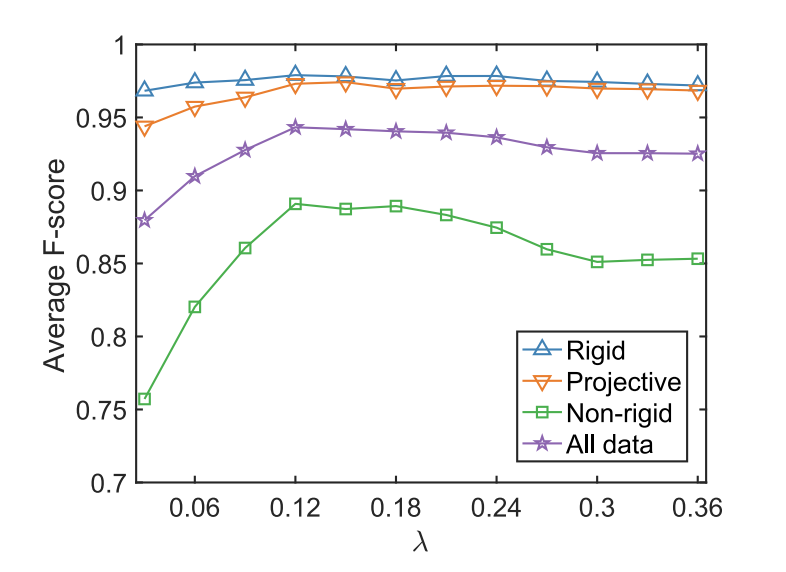
图5. 在从所选测试图像对中分类的各种类型的图像变换上，我们的方法的平均 F 分数具有不同的 λ 设置。

然后，验证了邻域构建的迭代过滤策略的有效性。图 6 总结了 30 个图像对的精度和召回率曲线，其中报告了在不同 λ 值的情况下没有和使用迭代过滤策略的 NMRC 的结果。迭代过滤策略显着提高了匹配性能。所提出的方法在适当的 λ 值（例如 0.12）下保留了大约 93.33% 的真实匹配，并且精度可以同时达到 95.74%。

pic6

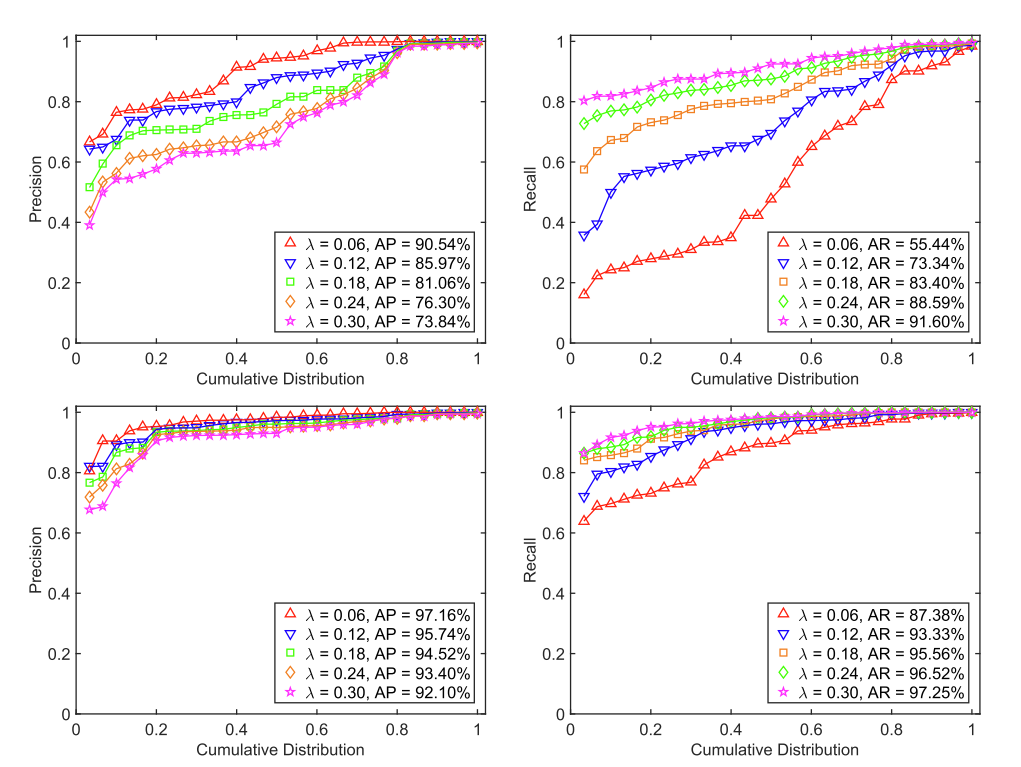
图6. 通过使用整个集合 S（顶部）和可靠集 UM（底部）在 30 个图像对上构建邻域{NxiK}i=1N\{\mathcal{N}_{x_i}^K\}_{i=1}^N和{NyiK}i=1N\{\mathcal{N}_{y_i}^K\}_{i=1}^N对累积分布的精确度和召回率使用不同的λ。曲线上坐标为 (x, y) 的点表示有 100 * x 百分比的图像对的精度或召回率不超过 y。 AP：平均精度； AR：平均召回率。

结果表明 κ = 10、K = 10 和 M = 3 被认为是它们的默认最优设置，可以达到最佳性能。考虑到参数 λ 的强烈影响，使用不同的 λ 对从选定的测试图像对中分类的各种图像变换测试平均 F 分数，结果如图 5 所示。这些结果表明考虑到各种类型的图像变换，λ 的最佳选择可能会略有变化。因此，λ = 0.12 被设置为其默认的最佳设置，因为它在所有数据上的平均 F 分数最好。请注意，通过使用网格搜索方法可以更准确地确定最佳参数。然而，所提出的方法中的大量参数（例如，超过 6 个）使得难以使用网格搜索。

还考虑了利用 I0 进行邻域建设的优点。为此，成本 ci 的分布在方程式 (10) 中报告，通过利用 S,UM 和 I0 进行图 7 中的邻域构建。由于存在受污染的数据，当使用整个假定集来构建邻域时，通常会在内部邻域中观察到几个异常值，如如图2（c）所示。因此，在离群点和离群点的分布之间没有找到明确的分界线。幸运的是，使用可靠的 UM 构建邻域可以显着扩大内点和异常点之间的边距。尽管如此，通过使用细化的 I0 进行邻域构建，进一步扩大了内点和异常点之间的边距。在参数 λ = 0.12 的情况下，30 个测试图像对的平均精度和召回率可以进一步从 (95.74%, 93.33%) 提高到 (96.84%, 97.03%)。值得注意的是，迭代地使用方程式（13）对于邻域构建直到收敛只能将平均精确召回对略微增加到（97.12％，97.34％）。但是，这种方法很耗时。

最后，如方程式 (13) 也起到了迭代过滤的作用，考虑使用不带UM的I0进行邻域构建。也就是说，使用 S 而不是 UM 进行邻域构建，得到 I0，然后在等式 (13) 估计中得到 I*。结果报告在图 7 的右下角，其中精确召回对仅为 (95.31%, 78.80%)。即使在迭代使用方程式 (13) 之后。对于直到收敛的邻域构建，最终的精确召回对为 (93.28%, 83.57%)，这大大低于使用 I0 和 UM 进行邻域构建时的结果 (96.84%, 97.03%)。因此，所提出的迭代过滤策略对于提高模型中的匹配性能至关重要。

pic7

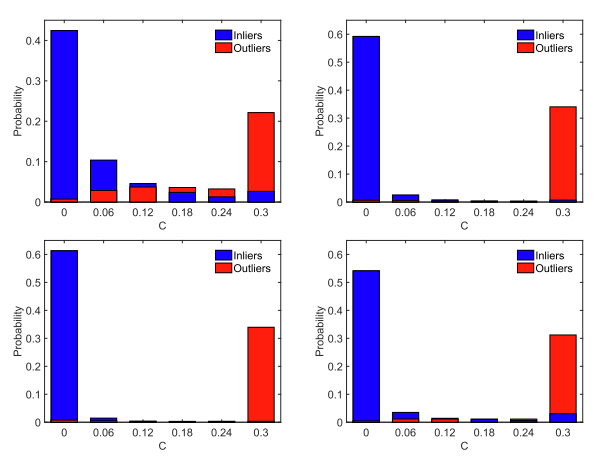
图7. 方程式中成本 ci 的分布。 (10) 使用整个集合S(左上)、UM(右上)、I0(左下)和没有UM的I0(右下)构造邻域结构{NxiK}i=1N\{\mathcal{N}_{x_i}^K\}_{i=1}^N和{CyiK}i=1N\{\mathcal{C}_{y_i}^K\}_{i=1}^N。

4.2 特征匹配结果

4.2.1 定性说明

选择了 10 个具有代表性的图像对来直观地说明 NMRC 的匹配性能，结果如图 8 所示。这些图像对涉及不同类型的变换，包括仿射（第 1 次）、非刚性变形（第 2 次、第 3 次） , 第 4 和第 5) 和对极几何 (第 6、第 7、第 8、第 9 和第 10)。对于每组的结果，左图示意性地展示了匹配结果，右图是推定匹配的向量场表示。 Precision、recall 和 F-score 用于表征匹配性能，其中 F-score 定义为 2 × Precision × Recall 和 Precision + Recall 的比值。手动检查每个图像对中的每个试探匹配以建立基本事实，并在进行实验之前提供基准以确保其客观性。使用NMRC，10个图像对的精度、召回率和Fscore统计如下：(99.66%, 100.0%, 99.83%), (99.57%, 96.23%, 97.87%), (97.68%, 96.99% , 97.34%),(99.01%, 100.0%, 99.50%), (94.83%, 90.66%, 92.30%),(96.67%, 90.14%, 93.43%), (98.35%, 100.0%, 99.17%),( 98.45%、99.22%、98.83%）、（95.71%、95.71%、95.71%）和（100.0%、100.0%、100.0%）。这些结果表明，大多数真实的对应关系都被成功确定，在所有测试图像对上只有很少的误判。这一发现还验证了 NMRC 足够强大，可以处理各种类型的转换，尽管存在大量异常值。

pic8

图8. 我们的 NMRC 在 10 个代表性图像对上的特征匹配结果。从上到下和从左到右：Land、Cubebreadtoychips、Book、Retina、T 恤、Church、Bear、Herzjesu、Frustum 和 Sene。 10 对图像的推定匹配数分别为 2203、327、746、183、300、126、198、196、400 和 250。 10个图像对中的内点比例分别为13.21%、73.09%、75.74%、54.64%、60.67%、56.35%、90.40%、65.31%、31.25%和52.80%。运动场中每个箭头的头部和尾部对应于两幅图像中特征点的位置（蓝色=真阳性，黑色=真阴性，绿色=假阴性，红色=假阳性）。为了可见性，在图像对中，最多显示 100 个随机选择的匹配项，并且不显示真正的否定项。

4.2.2 定量比较

在五个具有代表性的数据集（Ma et al., 2021）上进行了实验，即 Daisy、DTU、Adelaide（Wong et al., 2011）、RS 和 Retina，以提供全面的性能比较。具体来说，Daisy 包含带有真实深度图的宽基线图像对，包括两个短图像序列和几个单独的图像对，从中创建了总共 52 个图像对用于评估。 DTU 包含大量具有真实相机位置的不同场景，从中选择两个场景（即 Frustum 和 House）来创建 131 个涉及大视点变化的图像对进行评估。阿德莱德包含 38 个图像对，其中包括多个不同建筑物的图像对，主要与极线几何尝试有关，以及多个具有多种运动的图像对，即多个物体存在并在两个图像之间进行独立运动。 RS 是一个遥感数据集，包含 161 个图像对，包括彩色红外、SAR 和全色照片。 Retina 是一个医学图像数据集，包含 70 个涉及非刚性变换的视网膜图像对。

假定集中的前三个公开可用数据集的特征对应的正确性是根据相应数据集提供的基本事实来确定的。考虑到前面提到的基准，建立剩余数据集的真实对应关系。特别地，手动检查每个图像对的每个特征对应的正确性。

采用了九种最先进的鲁棒特征匹配方法进行比较：RANSAC (Fischler and Bolles, 1981), MLESAC (Torr and Zisserman, 2000), MAGSAC++ (Barath et al., 2021), ICF (Li and Hu, 2010), GS (Liu and Yan, 2010), GMS (Bian et al., 2020), LPM (Ma et al., 2019), mTopKRP (Jiang et al., 2019), and LFGC (Moo Yi等人，2018）。这些替代方案涵盖了文献中的不同类别，因此是特征匹配领域的合适代表。需要指出的是，RANSAC、MLESAC 和 MAGSAC++ 使用了单应性模型，并且迭代次数设置为 10000 以平衡性能和效率。对于 RANSAC 和 MLESAC，确定内点的阈值设置为 3 个像素。对于 MAGSAC++，σmax 的设置考虑 50 个像素，这是原始论文中建议的。其余方法在原始论文的基础上实现，本研究的研究人员试图调整其参数以实现其最佳性能。此外，九种方法的参数在整个实验过程中都是固定的。

pic9

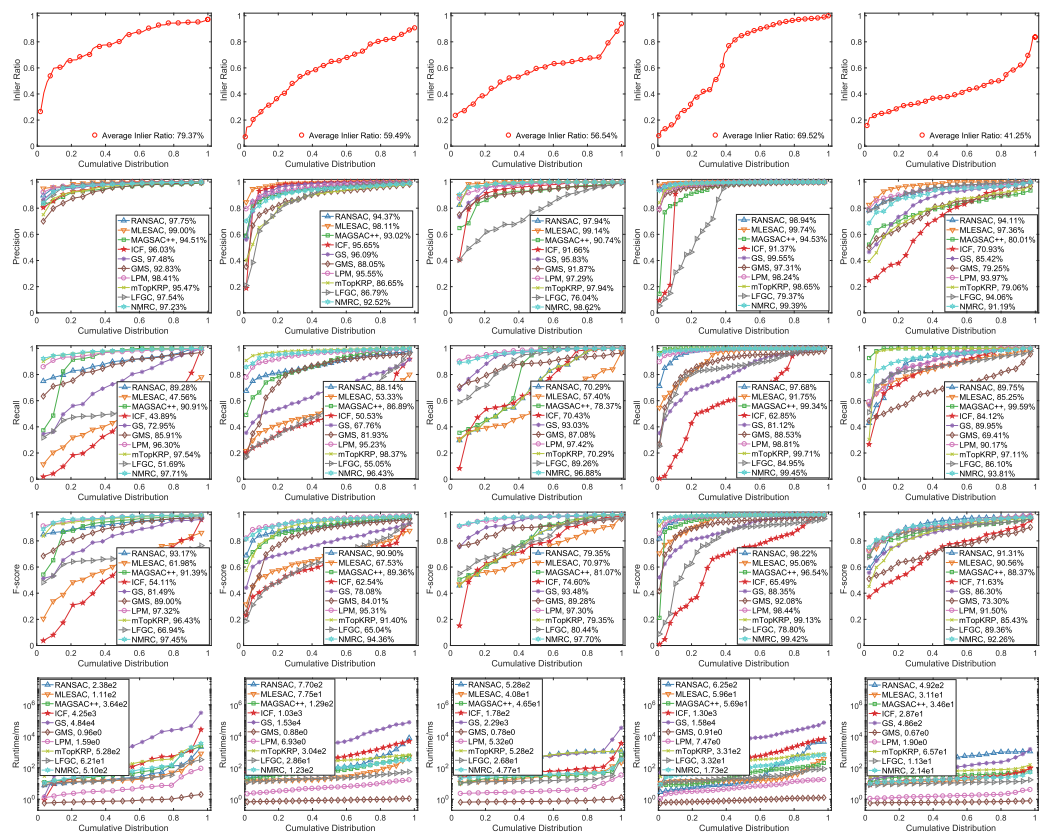
图9. RANSAC、MLESAC、MAGSAC++、ICF、GS、GMS、LPM、mTopKRP、LFGC 和 NMRC 在五个数据集上的定量比较，例如（从左到右）DAISY、DTU、Adelaide、RS 和 Retina。 （从上到下）相对于累积分布的初始内点比率、精度、召回率、F 分数和运行时间。

图 9 总结了五个数据集的初始内点率、精度、召回率、F 分数和运行时统计数据。值得注意的是，第四个数据集的内点率非常低，这使得不匹配消除变得复杂。五个数据集上的平均试探对应数约为 1475.60、544.99、217.18、445.34 和 69.03。对于匹配性能，RANSAC 在 Daisy、DTU、RS 和 Retina 上的精度和召回率都令人满意。这种性能可能是由于花费了足够的采样时间来获取无异常值的子集来估计变换，尽管内点比率较低。 MLESAC 可以始终在所有数据集上实现最佳匹配精度，但考虑到 Daisy、DTU 和 Adelaide 的召回率，其表现不佳。这种性能是通过利用最大似然过程来验证模型质量而不是仅仅通过内点数来实现的，这可以提高精度但同时牺牲召回率。 MAGSAC++ 在 RS 和 Retina 上的召回表现良好，但在 Retina 上的精度表现不佳。值得注意的是，RANSAC、MLESAC 和 MAGSAC++ 在Adelaide的表现都很差，因为它们无法处理严重的非刚性变换。考虑到精确度或召回率，ICF 通常具有可观的性能，但并非同时如此。这个结果可能是由于 ICF 假设运动场是全局平滑的，它无法处理深度不连续或运动不一致的场景。 GS 在 Adelaide 上取得了令人满意的性能，但在其余数据集上表现不佳，因为它不能自动估计亲和矩阵的因子及其非仿射不变性。 GMS 的性能并不能令人满意，尤其是在 Retina 数据集上，因为它最初是设计有相当数量的试探性对应关系来实现改进的性能。 LFGC 通常会产生令人满意的精度结果。然而，召回率非常低，因为它主要旨在识别良好的对应关系并同时准确地恢复相对姿势。因此，LGFC 可能会错误地删除一组不稳定的真实对应，从而导致召回率低。此外，一些涉及非刚性变形或低重叠区域的测试数据与LFGC的训练数据有很大不同，后者通常会发生大规模或视点变化。此外，LFGC 需要相机内在函数作为输入来规范化数据，这在所提供的测试数据中是不可用的。

LPM 通常具有良好的性能，同时考虑到精度和召回率，因为它能够处理各种转换。 mTopKRP 在 Daisy 和 RS 上的表现相当不错，但在其余数据集上表现不佳。这样的性能是由于当图像对之间的变换相对简单时，通过排名列表距离测量有效地保留了邻域拓扑。但是，mTopKRP 将不再适用于复杂的非刚性变换。与上述方法相比，NMRC 可以有利地权衡精度与召回（即 F 分数），因为这种方法省去了图像对之间的运动模型，并完全捕获了输入数据的潜在内在几何形状。此外，这些方法的时间成本如图 9 所示，表明 NMRC 可以有效地消除错配。

4.2.3 稳健性测试

本节进一步验证了 NMRC 在不同变形程度下的性能，并与八种最先进的方法进行了比较。特别是，该方法在一组具有五种不同变形程度的图像上进行了测试，其中包含从图 10 中的 Daisy、DTU 和 VGG (Ma et al., 2021) 中选择的 8 个场景。值得注意的是，来自与第一列相比，从左到右被认为是变形程度增加。每行中的第一张图像与其余图像按顺序配对，为每个场景生成五个测试图像对。上述方法关于变形程度的内点率和 F-score 的平均值和标准偏差如图 11 所示。这些结果表明，所有方法的性能都随着变形程度的增加而退化，但建议的方法略有变化。因此，NMRC 具有很强的稳健性并优于其他竞争对手。

pic10

图10. 8个场景不同程度的变形。前两行从 DTU 中选择，第四和第五行从 Daisy 中选择，其余四行从 VGG 中选择。从左到右，第一列的变形程度逐渐增加。

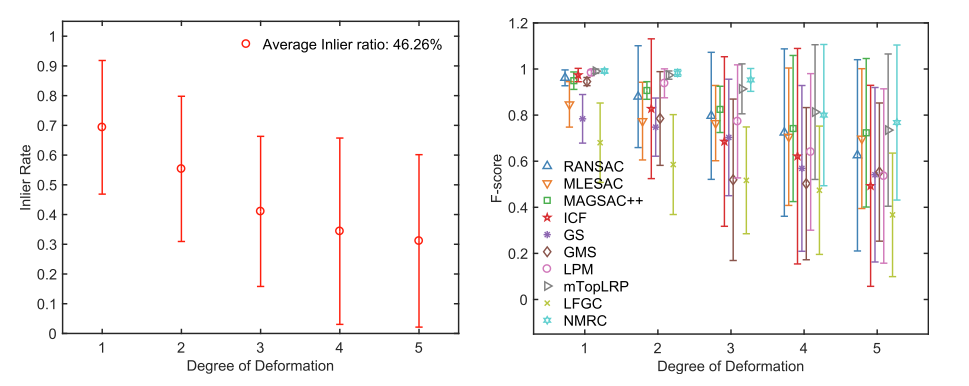
pic11

图11. 不同方法对变形程度增加的稳健性测试如图 10 所示。

4.3 遥感影像配准结果

图像配准是图像特征匹配最重要的应用之一。它侧重于扭曲的感测图像是否能够最大化参考图像和感测图像之间的重叠区域的对齐。因此，首先使用 NMRC 获取可靠的特征匹配。之后，考虑到监督学习中的通用性和平滑函数映射，选择薄板样条 (TPS) 通过估计变换函数 F 来生成特征匹配的平滑拟合 (Chui and Rangar ajan, 2003)。因此，这种方法可以解决特征匹配中的非刚性变换。此外，TPS 没有需要手动调整的自由参数，其封闭形式的解可以分解为全局线性仿射运动和局部非仿射翘曲分量。最后，使用估计的变换函数F\mathcal{F}将传感图像中的每个像素映射到相应的坐标。然后使用双三次插值算法计算参考图像中该坐标处的强度。

需要指出的是，在上述流程中，错配去除方法的召回率和精度都会显着影响配准结果。具体来说，如果精度低，剪枝后的对应响应中会包含大量异常值，这可能会导致 TPS 生成的平滑拟合函数出现偏差，导致配准失败。如果召回率低，修剪后的对应关系可能包含太少的内点，这使得生成的平滑拟合函数不能很好地表示全局变换，导致局部拟合误差很大。

为了清晰起见，图 12 显示了四个典型遥感图像对的一些直观配准结果。第一行表示原始输入图像，其中每组中的左侧和右侧分别是感测图像和参考图像。第二行报告NMRC的配准结果，其中每组的左右分别是棋盘格结果和扭曲的感知图像。这些结果表明，所提出的 NMRC 可以有效地对齐所有图像对的重叠区域，尤其是边缘区域。

pic12

图12. 我们的 NMRC 在 4 个具有代表性的遥感图像对上的整体图像配准的定性说明。顶部：原始输入图像，其中每组中的左右被感测和参考图像。底部：我们的 NMRC 的配准结果，其中每组的左右是 13 × 13 棋盘格结果和扭曲的感知图像。

选择六个遥感数据集作为测试数据集，对配准性能进行综合评价。前五个数据集来自 mTopKRP (Jiang et al., 2019)，即 UAV、SAR、PAN、CIAP 和 FE，分别经历射影、相似或刚性、仿射或射影、刚性和非刚性。此外，720 yun (Liang et al., 2020) 用于非刚性测试。从上述数据集中选择包含不同类型转换的 87 个图像对进行评估。这些图像对的平均初始对应数约为 1,080.99，内点率仅为 27.07%。均方根误差 (RMSE)、最大误差 (MAE) 和中值误差 (MEE) 用于测量图像配准的准确性，定义如下：

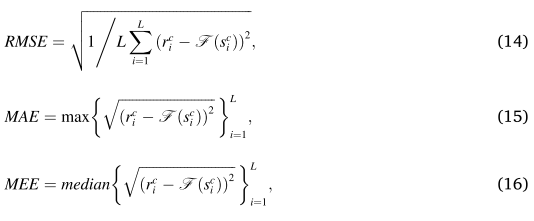
form14

其中ricr_i^c和sics_i^c分别是参考图像和感知图像的相应界标（即像素坐标），F\mathcal{F}是从感知图像到参考图像的估计变换函数，L表示所选界标的数量，max(· ) 和 median(⋅) 分别返回集合的最大值和中值。此外，定量实验是在选定的地标{ric,sic}i=1L\{r_i^c,s_i^c\}_{i=1}^L上手动进行的，性能评估是通过计算分布在感兴趣区域周围易于识别的位置的 20 对地标的 RMSE、MAE 和 MEE 来衡量的。

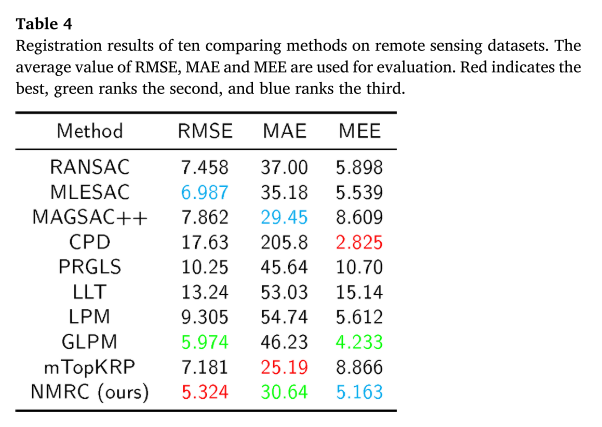
table4

表4（由于错误对应的存在，可能会导致局部拟合误差较大，从而导致较高的标准偏差）报告了 87 个选定图像对的统计结果。使用九种代表性方法进行比较，包括 RAN SAC (Fischler and Bolles, 1981)、MLESAC (Torr and Zisserman, 2000)、MAGSAC++ (Barath et al., 2021) ), CPD (Myronenko and Song, 2010), PRGLS (Ma et al., 2016), LLT (Ma et al., 2015), LPM (Ma et al., 2019), GLPM (Ma et al., 2018) , 和 mTopKRP (Jiang et al., 2019)。表格显示，NMRC 可以达到 RMSE 的最佳性能，MAE 的第二佳性能和 MEE 的第三佳性能。 CPD 获得了最好的 MEE 性能，其次是 GLPM 和 NMRC。然而，由于 RMSE 和 MAE 的指标较差，CPD 不足以应对图像配准任务。 RANSAC、MLESAC 和 MAGSAC++ 由于其全局几何约束而实现了稳定的性能，但未能解决非刚性变形。 LLT 和 PRGLS 的性能相对较差主要是由于假定的内点率较低。此外，出于同样的原因，LPM 表现不佳，即由于其不严格的测量标准，可能会保留一些粗略的异常值。 mTopKRP 具有最好的 MAE 性能，并且由于 K-NN 排名列表度量，考虑 RMSE 时表现相对较好。同时，由于其引导匹配策略，GLPM 也具有相当可观的性能。所提出的NMRC方法可以实现最令人满意的性能。

4.4 闭环检测结果

闭环检测 (LCD) 需要正确识别环境中先前访问过的区域，是视觉 SLAM 系统的重要组成部分 (Zhang et al., 2021)。现有的 LCD 方法通常应用 RANSAC 来验证闭环对，因为它能够同时建立可靠的对应关系并估计图像对之间的转换。然而，RANSAC 依赖于预定义的参数模型，无法处理复杂的变换，例如非刚性变形。

因此，RANSAC 被用作基线来证实用于验证 LCD 任务候选帧的 NMRC 的有效性。特别是，使用相当流行的词袋（BoW）来选择闭环候选以减少计算需求，然后采用不匹配去除方法来建立图像对应关系以检测闭环对。选择了三个公开可用的数据集（Zhang 等人，2021），即 KITTI 02、St1210 和 Malaga 2009 Parking 6L (Malaga)，总结在表 5 中，以对该任务进行综合评估。

4.4.1 定性说明

首先，为了视觉清晰，给出了一些关于 NMRC LCD 性能的定性结果。根据里程计记录的数据，每个数据集上的机器人轨迹用图 13 的黑线绘制。闭环对标记为红色空心点，同时用蓝线连接它们。绿色实心点是真阳性检测的具体说明。

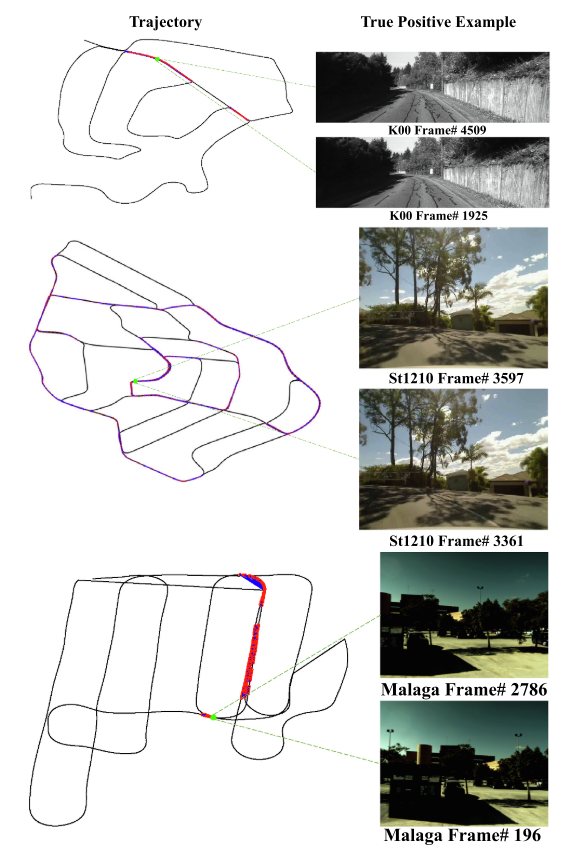
pic13

图13. LCD 任务的插图。从上到下：KITTI 02、St1210 和马拉加。从左到右：机器人的轨迹和真正的正例。在每一行的左边，黑色轨迹是从 GPS 日志中获得的，在 100% 精度下，在最大召回率下获得闭环识别结果。闭环对被标记为红色空心点，同时使用蓝线连接它们。绿色实心点是真阳性检测的具体说明。 （有关此图例中颜色参考的解释，请读者参考本文的网络版本。）

4.4.2 定量比较

LCD 系统中算法验证的闭环提供了不精确的信息，从而引发整个系统不可避免的性能下降，尤其是当 LCD 模块认为假闭环对为真时。同时，理想的 LCD 模块应该具有高召回率，即检测尽可能多的闭环对。因此，最大召回率是准确率100%时算法性能的重要评价指标。

比较结果总结在表 6 中。使用 RANSAC、MLESAC、MAGSAC++、GMS、LPM 和 mTopKRP 等六种错配去除方法进行比较。该表显示，NMRC 可以在三个数据集中的两个（即 KITTI 02 和 Malaga）上实现 100% 精度的最高召回率。虽然 NMRC 在 St1210 上与 GMS 相比表现略差，但所提出的方法仍然排名第二，达到了相当令人满意的水平。总体而言，NMRC 可以在不同的数据集上实现最稳定的性能。

pic14

图14. LPM、mTopKRP 和提议的 NMRC 等松弛（例如，邻域感知）方法无法区分相当稀疏区域（即 NMRC 结果中包含假阴性的局部区域）中的内点和异常点的失败案例。

5. 总结

本文提出了一种基于两个特征集之间潜在真实匹配的稳定局部拓扑结构的鲁棒特征匹配方法NMRC。每个假定对应的邻域表示是基于流形学习获得的，然后使用 L2 范数的平方来衡量邻域流形表示的一致性。特别是，设计了一种基于邻域相似度的迭代过滤策略，以在数据严重恶化的情况下提高鲁棒性。同时，将该思想表述为数学模型，推导出具有线性时间复杂度的闭式解。一般特征匹配和两个现实世界任务的实验结果表明，所提出的策略优于最先进的竞争对手。

值得注意的是，尽管邻域流形表示非常有效，但这种表示依赖于良好的初始化来捕获局部区域中足够可靠的对应关系。这将支持构建更准确的邻域流形表示。幸运的是，在建议的迭代过滤策略下，它适用于大多数情况。然而，当假定的对应关系在局部区域非常稀疏时，这种策略将受到限制，这可能会导致表示邻域流形的困难。请注意，这是松弛方法的常见问题，例如 LPM (Ma et al., 2019) 和 mTopKRP (Jiang et al., 2019)，它们源自局部共识假设。图 14 中显示了一个失败案例，这表明 LPM、mTopKRP 和提议的 NMRC 无法区分具有极稀疏假定对应关系的局部区域的内点和异常点。尽管如此，提议的NMRC仍然具有更好的整体性能。未来的研究将集中在设计更好的特征匹配器以建立更有效的假定对应关系，并充分利用局部和全局几何信息来处理这种情况。

补充

一致流形逼近与投影（UMAP）是一种降维技术，它可以用于可视化，类似于t-SNE，但也可以用于一般的non-linear维数缩减。

论文翻译
#论文翻译 #特征匹配 #邻域拓扑一致 #NMRC #最小化重构误差 #邻域流形
NMRC：基于邻域流形表示一致性的鲁棒特征匹配
http://example.com/2022/06/07/NMRC：基于邻域流形表示一致性的鲁棒特征匹配/
作者
Mr.Yuan
发布于
2022年6月7日
许可协议