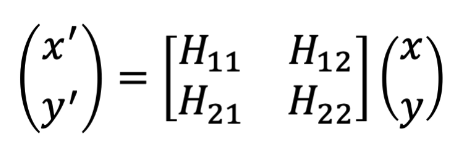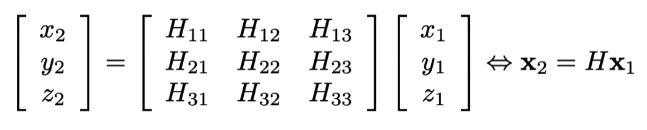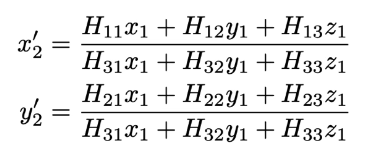基于重采样的匹配算法笔记

1. RANSAC 随机抽样一致

随机抽样一致性算法（RANSAC）

它可以从一组包含“局外点”的观测数据集中，通过迭代方式估计数学模型的参数。它是一种不确定的算法——它有一定的概率得出一个合理的结果；为了提高概率必须提高迭代次数。

RANSAC最本质的目标是拟合曲线。

1.1 步骤

一个简单的例子是从一组观测数据中找出合适的2维直线。假设观测数据中包含局内点和局外点，其中局内点近似的被直线所通过，而局外点远离于直线。简单的最小二乘法不能找到适应于局内点的直线，原因是最小二乘法尽量去适应包括局外点在内的所有点。相反，RANSAC能得出一个仅仅用局内点计算出模型，并且概率还足够高。但是，RANSAC并不能保证结果一定正确，为了保证算法有足够高的合理概率，我们必须小心的选择算法的参数。

1. 从样本集中随机选取一组可以计算模型参数的子样本（如果拟合线性则是两个点，若是抛物线则是三个点），计算得到的模型参数
2. 判断模型参数的质量（判断该模型下的局内点与局外点，局内点越多说明模型越好）
3. 重复上述步骤，记录质量最好的模型；满足迭代条件时退出（达到迭代次数）

1.2 相关参数

p表示迭代过程中出现好的模型的概率（即用于计算模型参数的点均为局内点）

w=局内点的数目/数据点的总数目(w未知)

计算模型参数需要n个点：

​ n个点中至少有一个点为局外点的概率：$1-w^n$

则：

$1-p=(1-w^n)^k$

k为迭代次数，则当k趋向于无穷大时，p趋向于1

1.3 优缺点

RANSAC的优点是它能鲁棒的估计模型参数。例如，它能从包含大量局外点的数据集中估计出高精度的参数。

RANSAC的缺点是它计算参数的迭代次数没有上限；如果设置迭代次数的上限，得到的结果可能不是最优的结果，甚至可能得到错误的结果。RANSAC只有一定的概率得到可信的模型，概率与迭代次数成正比。

RANSAC的另一个缺点是它要求设置跟问题相关的阀值。

RANSAC只能从特定的数据集中估计出一个模型，如果存在两个（或多个）模型，RANSAC不能找到别的模型。

1.4 RANSAC去除错误匹配点对

设原图像提取出的特征点为$T=\{t_1,t_2,..\}$，待匹配图像提取出的特征点为$S=\{s_1,s_2,..\}$

通过特征点描述符进行匹配后得到匹配点对集：$match=\{t_1,s_1;t_2,s_2;..\}$

1. 随机在匹配点对集中选取n个参数（拟合线性则为2，抛物线则为3，等等）
2. 计算模型参数得到$f(t)$
3. 将剩余的t代入$f(t)$中计算$s'$，然后计算$s与s'$的误差，若小于设定阈值，则为局内点，以此判断模型的好坏
4. 重复上述步骤，记录质量最好的模型；满足迭代条件时退出（达到迭代次数）

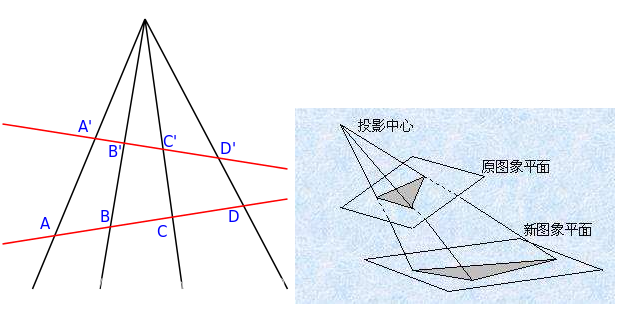
1.5 RANSAC计算单应性矩阵

单应性矩阵：

两个不同视角的图像上的点对的齐次坐标可以用一个射影变换表述，即：x1 = H*x2

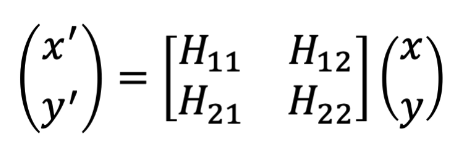
其中H即为单应性矩阵

为了增加平移变换，将二维坐标的点（x，y）变为齐次坐标系（x，y，z）

则单应性矩阵具体写为：

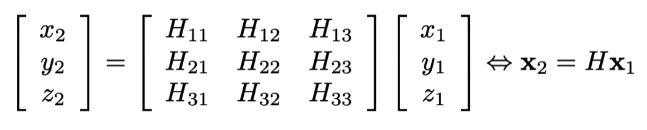
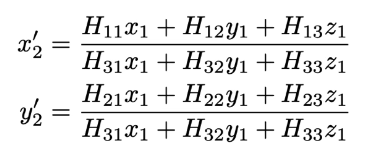
将z1设为1，则有8个方程需要求解，所以至少需要4对点。根据RANSAC去除错误点对后的$match'$对矩阵求解即可。

需要注意的是，这种单应性矩阵只适合刚性变换的图像，当图像出现非刚性变换时效果不好。

2. MAGSAC 边缘化样本一致

CVPR 2019 Open Access Repository (thecvf.com)

MAGSAC：Marginalizing Sample Consensus

danini/magsac: The MAGSAC algorithm for robust model fitting without using an inlier-outlier threshold (github.com)

2.1 符号定义

• $P$：数据点集
• $\theta$：模型参数
• $I$：内点选择器函数
• $F$：拟合函数
• $\tau(\sigma)$：内外点区分阈值（异常值阈值）
• $\sigma$：噪声标准差
• $D$：残差函数
• $Q$：模型质量函数
• $m$：最小样本量
• $\sigma_{max}$：最大噪声标准差（用户定义的最大噪声标度）

数据点集$P=\{p\ |\ p\in \R^k,k\in\N_{>0}\}$，其中k是维度。

内点集 $\mathcal{I}\subseteq P$

要拟合的模型由其参数向量$\theta\in\Theta$表示，其中$\Theta=\{\theta\ |\ \theta\in\R^d,d\in\N_{>0}\}$是流形，例如，所有可能的2D线中，d是模型的尺寸，例如d = 2 用于 2D 线（角度和偏移）。

拟合函数$F$：$P^*\to \Theta$，从$n\geq m$点中计算模型参数，其中$P^*=exp(P)$是 P 的幂集，m 是拟合模型的最小点数，例如m = 2 用于 2D 线。请注意，F 是根据输入集应用不同估计量的组合函数，例如，如果 n = m 则为最小方法，否则为最小二乘拟合。

残差函数$D:\Theta\times P\to\R$是点到模型的残差函数（？）

内点选择器函数$I:P^*\times\Theta\times\R\to P^*$给定模型$\theta$和阈值$\sigma$后选择的内点。例如，如果考虑原始的 RANSAC 方法，则

$I_{RANSAC}(\theta,\sigma,P)=\{p\in P|D(\theta,p)<\sigma\}$

模型质量函数$Q:P^*\times\Theta\times\R\to\R$更高的质量被解释为更好的模型。

对于RANSAC，则

$Q_{RANSAC}(\theta,\sigma,P)=|I(\theta,\sigma,P)|$

2.3 边缘化样本一致

在本节中，提出了一种称为MAGSAC的方法，该方法从类似RANSAC的鲁棒模型估计中消除了阈值参数。

2.3.1 $\sigma$边缘化

让我们假设噪声$\sigma$是具有密度函数$f(σ)$的随机变量，并让我们为模型$ θ $在$ σ $上边缘化定义一个新的质量函数，如下所示：

$Q^*(\theta,P)=\int Q(\theta,\sigma,P)f(\sigma)d\sigma$

在没有先验信息的情况下，我们假设 σ 是均匀分布的，$\sigma\sim\mathcal{U}(0,\sigma_{max})$，于是有

$Q^*(\theta,P)=\frac{1}{\sigma_{max}}\int_0^{\sigma_{max}} Q(\theta,\sigma,P)d\sigma$

举个例子，对于普通的RANSAC，用$ Q(\theta,\sigma,P)$表示内点数，其中$\sigma$是内外点阈值，${D(\theta,p_i)}_{i=1}^{|P|}$是模型$ θ $的距离，使得$0\leq D(\theta,p_1)<D(\theta,p_2)<..<D(\theta,p_K)<\sigma_{max}<D(\theta,p_{K+1})<...<D(\theta,p_{|P|})$，则我们得到一个质量函数：（内点个数K - 内点残差的归一化）

$Q^*(\theta,P)=K-\frac{1}{\sigma_{max}}\sum_{k=1}^K D(\theta,p_k)=\sum_{k=1}^K(1-\frac{D(\theta,p_k)}{\sigma_{max}})$

假设内点和外点的分布是均匀的$(内点\sim\mathcal{U}(0,\sigma);外点\sim\mathcal{U}(0,l))$,利用$θ$模型的对数似然性作为其质量函数Q，我们得到:（？）

$Q^*(\theta,P)=K(\mathrm{ln}\frac{l}{\sigma_{max}}+1)-\frac{1}{\sigma_{max}}\sum_{k=1}^KD(\theta,p_k)(1+\mathrm{ln}\frac{l}{D(\theta,p_k)})-|P|\mathrm{ln}l$

通常，内点的残差被计算为在某个 ρ 维空间中与模型的欧几里德距离。 如果假设沿该 ρ 维空间的每个轴的距离误差是独立的并且具有相同方差$ σ^2 $的正态分布，则$（残差）^2/σ2 $具有 ρ 自由度的卡方分布。 所以，

$g(r|\sigma)=2C(\rho)\sigma^{-\rho}exp(-r^2/2\sigma^2)r^{\rho-1}$

是内点残差的密度,且

$C(\rho)=\frac{1}{2^{\rho/2}\Gamma(\rho/2)}$

其中

$\Gamma(a)=\int_0^{+\infty}t^{a-1}exp(-t)dt$

在MAGSAC中，内点的残差由密度分布$g(r|\sigma)$描述，外点由区间$[0,l]$上的均匀分布描述。

请注意，对于图像，$l$ 可以设置为图像对角线(?)。 内点-异常值阈值$\tau(\sigma)$设置为密度分布$g(r|\sigma)$的 0.95 或 0.99 分位数。因此，给定 $σ$ 的模型 $θ$ 的可能性为

$L(\theta,P|\sigma)=\frac{1}{l^{|P|-|\mathcal{I}(\sigma)|}}\Pi_{p\in\mathcal{I}(\sigma)}\big[2C(\rho)\sigma^{-\rho}exp(\frac{-D^2(\theta,p)}{2\sigma^2})D^{\rho-1}(\theta,p)\big]$

对于给定σ，MAGSAC使用模型θ的对数似然作为其质量函数，如下所示:

$Q(\theta,\sigma,P)=\mathrm{ln}L(\theta,P|\sigma)$

因此，σ上边缘化的质量函数如下：

$Q^*_{MAGSAC}(\theta,P)=\frac{1}{\sigma_{max}}\int_0^{\sigma_{max}}\mathrm{ln}L(\theta,P|\sigma)d\sigma\\ \approx-|P|\mathrm{ln}l+\frac{1}{\sigma_{max}}\sum_{i=1}^K[i(\mathrm{ln}2C(\rho)l-\rho\mathrm{ln}\sigma_i)-\frac{R_i}{\sigma_i^2}+(\rho-1)Lr_i](\sigma_i-\sigma_{i-1})$

其中，$\{D(\theta,p_i)\}_{i=1}^{|P|}$是模型$\theta$的距离，$\sigma_0=0$且

$0\leq D(\theta,p_1)=\tau(\sigma_1)<D(\theta,p_2)=\tau(\sigma_2)<...\\<D(\theta,p_K)=\tau(\sigma_K)<\tau(\sigma_{max})<D(\theta,p_{K+1}<...<D(\theta,p_{|P|}),\\R_i=\frac{1}{2}\sum_{j=1}^iD(\theta,p_j)^2 \\Lr_i=\sum_{j=1}^i\mathrm{ln}D(\theta,p_j)$

因此，所提出的新质量函数 $Q^*_{MAGSAC}$ 不依赖于手动设置的噪声水平 σ。

2.3.2 $σ$-一致模型拟合

由于没有一组可用于改进从最小样本获得的模型的内点，因此我们建议使用加权最小二乘拟合，其中权重是内点的点概率。

假设给定从最小样本估计的模型 $θ$。使$\theta_\sigma=F(I(\theta,\sigma,P))$为使用输入模型$\theta$周围的$\tau(\sigma)$选定的内部集合$I(\theta,\sigma,P)$所隐含的模型.

则点$p\in P$在给定模型$\theta_\sigma$内的概率是：

$L(p|\theta_\sigma,\sigma)=2C(\rho)\sigma^{-\rho}D^{\rho-1}(\theta_\sigma,p)exp(\frac{-D^2(\theta_\sigma,p)}{2\sigma^2})$

为了找到一个可能成为内点的点，使得比 σ 更边缘化，使用与以前相同的方法:

$L(p|\theta)\approx \frac{2C(\rho)}{\sigma_{max}}\sum_{i=1}^K(\sigma_i-\sigma_{i-1})\sigma_I^{-\rho}D^{\rho-1}(\theta_\sigma,p)exp(\frac{-D^2(\theta_\sigma,p)}{2\sigma_i^2})$

使用加权最小二乘法估计改进模型$\theta_{MAGSAC}^*$，其中点$p\in P$的权重是$L(p|\theta)$

2.3.3 终止标准

没有一个独立的集合，因此，至少一个粗略估计的独立比率，使得RANSAC的标准终止准则不适用，其如下:

$k(\theta,\sigma,P)=\frac{\mathrm{ln}(1-\eta)}{\mathrm{ln}(1-(\frac{|I(\theta,\sigma,P|)}{|P|})^m)}$

其中 k 是迭代次数，$η$ 是手动设置的结果置信度，m 是估计所需的最小样本的大小，$|I(θ, σ, P)| $是迄今为止最好的模型的内点数。(与RANSAC类似)

为了在不使用特定$σ$的情况下确定k，将其边缘化是一个简单的选择，类似于模型质量。具体如下：

$k^*(P,\theta)=\frac{1}{\sigma_{max}}\int_0^{\sigma_{max}}k(\theta,\sigma,P)d\sigma\\ \approx\frac{1}{\sigma_{max}}\sum_{i=1}^{k}\frac{(\sigma_i-\sigma_{i-1})\mathrm{ln}(1-\eta)}{\mathrm{ln}(1-(\frac{I(\theta,\sigma_i,P)|}{|P|})^m)}$

因此，在过程中计算MAGSAC所需的迭代次数，并在找到新的sofar-the-best模型时进行更新，类似于RANSAC。

2.4 使用 σ 一致的算法

在本节中，我们提出了两种应用 σ 一致的算法。 首先，MAGSAC 将结合提议的边缘化方法、加权最小二乘法和终止标准进行讨论。 其次，提出了一个后处理步骤，该步骤适用于每个鲁棒估计器的输出。 在实验中，它总是在处理时间没有明显恶化的情况下改进输入模型，最多增加几毫秒。

2.4.1 加快程序

由于普通的 MAGSAC 会多次应用最小二乘拟合，因此隐含的计算复杂度会相当高。 因此，我们提出了加速该过程的技术。为了避免不必要的操作，我们引入了一个 $\sigma_{max}$ 值，并且在优化过程中只使用小于$\sigma_{max}的\sigma$。这个 $\sigma_{max}$ 可以设置为一个相当大的值，例如 10 个像素。在结果表明$\sigma_{max}$太低的情况下，例如如果残差的密度模式接近$\sigma_{max}$，则可以使用更高的值重复计算。

我们没有计算每个$\sigma_i$的$\theta_{\sigma_{i}}$，而是将这些$\sigma$的范围统一划分为d个分区。因此，处理后的 σ集如下：

$\sigma_1+(\sigma_{max}-\sigma_1)/d,\sigma_1+2(\sigma_{max}-\sigma_1),..,\sigma_1+(d-1)(\sigma_{max}-\sigma_1)/d,\sigma_{max}$

通过这种简化，最小二乘拟合的数量从 K 下降到 d，其中 d ≪ K。在实验中，d 设置为 10。

此外，正如为 USAC 提出的那样，有几种方法可以提前跳过对没有机会比以前最好的模型更好的模型的评估。为此，我们应用带有$\tau_{ref}$ 阈值的 SPRT。阈值$\tau_{ref}$不用于模型评估或内部选择步骤，而仅用于在不必要时跳过应用 σ 一致。在实验中，$\tau_{ref}$设置为 1 个像素。

最后，σ-consensus 的并行实现可以直接在 GPU 或多个 CPU 上完成，在不同的线程上评估每个 σ。在我们的 C++ 实现中，它运行在多个 CPU 内核上。

2.4.2 $\sigma$一致算法

建议的 σ 一致在算法1中进行了描述，输入参数为：数据点（P）、初始模型参数（θ）、用户定义的分区数（d）和σ的限制（$\sigma_{max}$）。

作为第一步，该算法采用比初始模型更接近的点$\tau(\sigma_{max})$（第一行）。函数 $\tau$返回由输入$\sigma$参数隐含的阈值。在 $\chi^2$分布的情况下， $τ(σ) = 3.64σ$。 然后对内点的残差进行排序，因此，在$\{\sigma_i\}_{i=1}^{|\mathcal{I}|}$中，$\sigma_i<\sigma_j\Leftrightarrow i<j$。

在$\mathcal{I}_{ord}$中，点的索引按顺序排列，以反映$\{\sigma_i\}_{i=1}^{|\mathcal{I}|}$，于是$\sigma_i=D(\theta,\mathcal{I}_{ord,i})/3.64$（第二行）。

在第3行和第4行中，权重初始化为零，$\sigma_{max}$设置为max（$\{\sigma_i\}_{i=1}^{|\mathcal{I}|}$）。然后计算当前σ范围。例如，要处理的第一个范围是$[\sigma_1,\sigma_1+\delta_\sigma]$。

请注意，$\sigma_1$= 0，因为在距模型零距离处至少有 m 个点。循环从第一个点运行到最后一个点，并且由于$\mathcal{I}_{ord}$是有序的，因此每个后续点都比之前的点离模型更远。直到当前范围的末尾，即分区，没有达到（第 7 行），它一个接一个地收集点（第 8 行）。超过当前范围的边界后，使用之前收集的所有点（第 10 行）计算$\theta_\sigma$。然后，对于每个点，权重由隐含概率更新（第 12 行）。最后，算法跳转到下一个范围（第 13 行）。在为每个点计算权重之后，应用加权最小二乘拟合来获得边缘化模型参数（第 14 行）。

2.4.3 MAGSAC

用σ-一致优化每个估计模型的MAGSAC程序见算法2.首先，它将模型质量初始化为零，并将所需的迭代次数初始化为$\infty$（第一行）。在每次迭代中，它选择一个最小样本（第 3 行），将模型拟合到所选点（第 4 行）验证它（第 5 行）并应用 σ-consensus 以获得在 σ 上边缘化的参数（第 6 行）。验证步骤包括简并度测试和停止评估模型的测试，如果没有机会比之前迄今为止最好的测试更好，例如通过SPRT测试。注意，对于SPRT，当计算与当前模型的距离时，验证步骤也包括在σ-一致性中（Alg.1中的第1行）。最后，计算模型质量（第8行），如果需要（第9行），则更新迄今为止的最佳模型和所需迭代次数（第10行）。作为对时间敏感的应用程序中的后处理步骤，σ 一致是优化RANSAC输出的一种可能选择，而不是对内点应用最小二乘拟合。在这种情况下，σ 共识仅应用一次，从而改善了结果，而t不会明显恶化。

3. MAGSAC++

IEEE Xplore Full-Text PDF:

MAGSAC++：一种快速、可靠、准确、鲁棒的估计器

4. NMRC 通过邻域流形实现鲁棒特征匹配

通过邻域流形表示共识进行鲁棒特征匹配 - ScienceDirect

5. GMS

GMS算法_

GMS-Feature-Correspondence:GMS特征对应算法的C++实现_

补充内容

1. 对极约束

2D-2D：对极约束

2. 基本矩阵

基本矩阵、本质矩阵和单应矩阵

3. 残差和误差

误差是观察值与真实值之间的差。经典测验理论（CTT）的基本假设是：X=T+E。也就是说，观察值等于真值加上误差。

残差是观察值与模型估计值之间的差。以回归分析为例，回归方程y=b0+b1x，当知道b0和b1时这就是一个真实的回归模型。比如y=2+3x。取一个数值（1,2），则模型估计值为y=2+3×1=5。残差为2-5=-3。因此，只要有一个确定的取值以及模型，则模型肯定有一个估计值，也就有一个残差了。

4. 均匀分布

在相同长度间隔的分布概率是等可能的。 均匀分布由两个参数a和b定义，它们是数轴上的最小值和最大值，通常缩写为$U（a，b）$。

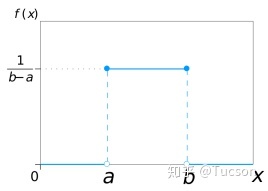
5. 卡方分布

三大抽样分布：卡方分布，t分布和F分布的简单理解

设$X_1,X_2,..,X_n\ \ i.i.d.\sim N(0,1)$，令$X=\sum_{i=1}^{n}X_i^2$，则称X是自由度为n的卡方变量，其分布称为卡方分布，记为$X\sim \chi_n^2$

设随机变量 X 是自由度为 n 的 χ2 随机变量, 则其概率密度函数为

$g_n(x)= \begin{cases} \frac{1}{2^{n/2}\Gamma(n/2)}x^{n/2-1}exp(-x/2)&,x>0\\ 0&,x\leq0 \end{cases}$

6. 边缘化

概率论之概念解析：边缘化（Marginalisation）

边缘化是一种方法，它要求对一个变量的可能值求和，以确定另一个变量的边缘贡献。这个定义可能听起来有点抽象，让我们用一个例子来说明这一点。

假设我们对天气如何影响英国人的幸福这一话题感兴趣。我们可以把它写成P(幸福|天气)，即给定天气类型的情况下一个人的幸福水平的概率是多少。

假设我们有测量一个人幸福所需的设备和定义，并记录了一个人所在的英格兰和另一个人所在的苏格兰的天气情况。现在，通常来说苏格兰人比英格兰人更幸福。问题是，人们总是有国籍的，所以在测量中我不能摆脱这个因素。所以我们实际测量的是P(幸福，国家|天气)，即我们同时关注幸福和国家。

边缘化告诉我们，如果我们把所有国家的可能性都加起来，我们可以计算出我们想要的数量(记住，英国是由三个部分组成的:英格兰、苏格兰和威尔士)，即P(幸福，国家=英格兰|天气)+ P(幸福，国家=苏格兰|天气)+ P(幸福，国家=威尔士|天气)。

而就是这样！边缘化告诉我们，只要把一些概率加起来就能得到所需的概率量。一旦我们计算出了答案(它可以是一个单个值或一个分布)，我们就可以得到我们想要的任何属性(推理)。

7. 条件概率密度

【概率论与数理统计】一个视频让你明白分布函数，概率密度函数，分布律，联合概率密度，联合分布函数，联合分布律，边缘概率密度，边缘分布函数都是什么意义和概念

条件概率密度函数：

$\begin{cases} f_{X|Y}(x|y)=\frac{f(x,y)}{f_Y(y)}\\ f_{Y|X}(y|x)=\frac{f(x,y)}{f_X(x)} \end{cases}$

边缘概率密度函数：

$\begin{cases} f_{X}(x)=\int{f(x,y)}dy\\ f_{Y}(y)=\int{f(x,y)}dx \end{cases}$

8. 复合概率密度函数

已知X的概率密度为$f_X(x)$，若有Y=f(x)，求Y的概率密度：

记X的累计概率为$F_X(x)$，Y的累计概率为$F_Y(y)$，则

$F_Y(y)=P\{Y\leq y\}=P\{f(X)\leq y\}=P\{X\leq f^{-1}(y)\}=F_X(f^{-1}(y))\\ \Rightarrow f_Y(y)=\frac{dF_X(f^{-1}(y))}{dy}=f_X(f^{-1}(y))\times (f^{-1}(y))’$