小波学习笔记

未完成版，过于难懂，应该参考理解傅里叶变换 - Blog of Mr.Yuan (ljy0109.github.io)

1、haar小波变换

1.1 小波背景知识

1.1.1 点的表达

1.1.1.1 点是一个数列

点是可数无穷维的点

在线性空间$l^2(Z),Z=(0,\pm1,\pm2,..)$中，存在点$P=(..,x_{-1},x_0,x_1,..)$

对于点P的限制为：$\sum_{l=-\infty}^{+\infty}|x_l|^2<+\infty$

即平方可和，能量有限，函数可积

1.1.1.2 点是一个函数

对于点$P=(..,x_{-1},x_0,x_1,..)$用坐标轴来表示

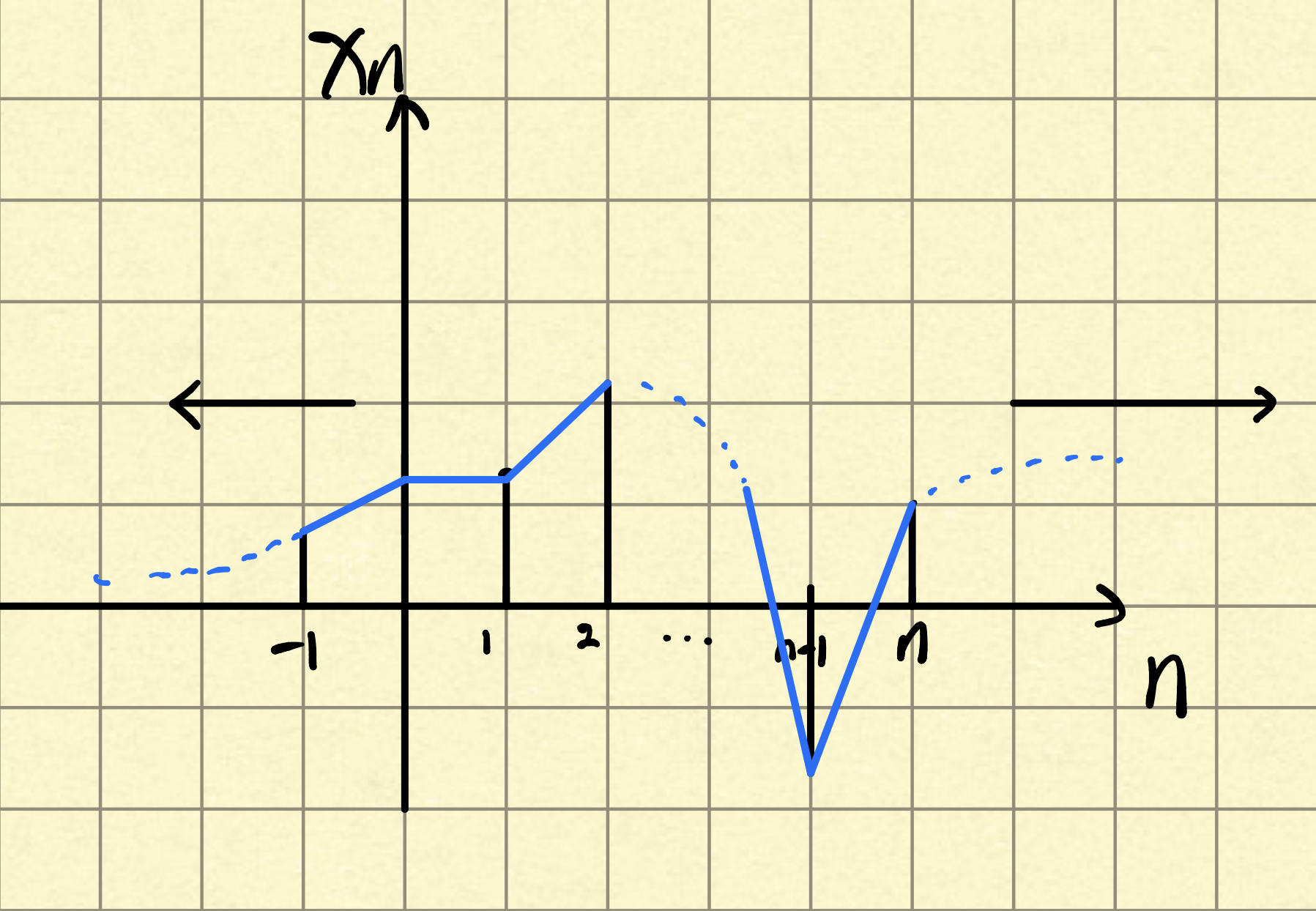
图中n为下标，xn为下标为n的x值。可以看出当点P为无穷维时，1和2之间的间距就会非常小，于是一个折线图就变成了一个连续的函数图像，且这个函数图像的积分小于无穷，即能量有限。

点的函数分两类：

第一类，周期函数：

$f(x+2\pi)=f(x)且\int_0^{2\pi}|f(t)|^2dt<+\infty$

将这些所有的f(x)（点）放在一个空间，记作$L^2(0,2\pi)$

第二类，非周期函数：

$\int_{-\infty}^{+\infty}|f(t)|^2dt<+\infty$

将这些所有的f(x)（点）放在一个空间，记作$L^2(-\infty,+\infty)$，又记作$L^2(\R)$

1.1.2 基向量

1.1.2.1 内积空间

1. 具有如下点内积或标量内积的实数域R上的欧式空间$\R^N$:

$\lang u,v\rang=u^Tv=u_0v_0+u_1v_1+..+u_{N-1}v_{N-1}=\sum_{i=0}^{N-1}u_iv_i\tag{2.1}$

​ 式中，u和v是N*1的列向量

2. 内积空间C([a,b]),其中向量是区间$a\leq x\leq b$上的连续函数，内积函数是积分内积（$f^*$表示共轭）

   $\lang f(x),g(x)\rang=\int_a^b f^*(x)g(x)dx \tag{2.2}$

1.1.2.2 正交基

在内积空间中，向量$z$的范数或长度定义为$||z||$，即

$||z||=\sqrt{\lang z,z\rang}\tag{2.3}$

并且两个非零向量z和w之间的夹角是

$\theta=arccos\frac{\lang z,w\rang}{\lVert z\rVert \lVert w\rVert}\tag{2.4}$

若z的范数是1，则称z是归一化的。若在式\eqref{eq4}中有${\lang z,w\rang}=0,\theta=90^。$,则称z和w是正交的。

则可进行如下定义，当且仅当：

$\lang w_k,w_l\rang=0,k\neq l\tag{2.5}$

时，非零向量$w_0,w_1,w_2..$是相互或两两正交的。它们是所张成内积空间的正交基。若基向量归一化，则它们是一个正交基且：

$\lang w_k,w_l\rang =\delta_{kl}=\begin{cases} 0,k\neq l\\ 1,k=l \end{cases} \tag{2.6}$

若

$\lang \tilde{w_k},w_l\rang=0,k\neq l \tag{2.7}$

则称向量集合$w_0,w_1,w_2,..$和对偶向量补集$\tilde{w_0},\tilde{w_1},..$是双正交的并且是所张成向量空间的一个双正交基。当且仅当：

$\lang \tilde{w_k},w_l\rang =\delta_{kl}=\begin{cases} 0,k\neq l\\ 1,k=l \end{cases} \tag{2.8}$

时，它们是双规范正交基。（对偶向量是指若向量a是一个可以使向量b映射成一个标量的映射，则a是b的对偶向量？）

令$W={w_0,w_1,..}$是内积空间V的一个正交基，并且令$z\in V$，则向量z可表示为基向量的线性组合：

$z=a_0w_0+a_1w_1+a_2w_2+... \tag{2.9}$

z与基向量$w_i$的内积为：

$\lang w_i,z\rang =\lang w_i,\alpha_0w_0+\alpha_1w_1+..\rang=\alpha_0\lang w_i,w_0\rang+\alpha_1\lang w_i,w_1\rang+..+\alpha_i\lang w_i,w_i\rang+.. \tag{2.10}$

由于$w_i$是相互正交的，所以式(2.10)右侧除了一项是非零外见式，其他都是0，则有:

$\alpha_i=\frac{\lang w_i,z\rang}{\lang w_i,w_i}$

若基向量的范数为1，则简化为

$\alpha_i=\lang w_i,z\rang$

1.1.3 傅里叶变换理论

一种拟合的思想

$f(t)=\sum_{k=-\infty}^{+\infty}\alpha_ke^{ikt}$

其中$e^{ikt}$可以理解为一系列的形如$e^{ix}$的波，通过改变k来实现波的拉伸，通过系数$\alpha_k$来实现波的权重

更进一步的写成：

$f(t)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}F(w)e^{iwt}dt$

这里的一个问题是，傅里叶变化中$e^{ikt}$波在现实中是不存在的，不合理的

1.1.4 哈尔Haar变化

哈尔变化则是把$e^{ikt}$换成了h(t):

$h(t)= \begin{cases} \frac{1}{\sqrt{2}}&,0\leq x<\frac{1}{2}\\ -\frac{1}{\sqrt{2}}&,\frac{1}{2}\leq x<1\\ 0&,其他 \end{cases}$

更进一步定义了$h_{j,k}(t)$:

$h_{j,k}(t)=2^{\frac{j}{2}}h(2^jt-k),(j,k)\in\Z^2$

(j,k)取遍所有的整数，k表示小波的平移，j表示小波的缩放。j增大则小波变窄，幅值增大；j取负值则使小波变长，幅值变小（此处有能量恒定的意思，即任意拉伸，能量始终不变（波的面积不变））。$h_{j,k}(t)$是标准正交基，则：

$f(t)=\sum_j\sum_k \alpha_{j,k}h_{j,k}(t)$

1.1.5 窗函数(Gabor,1946)

$\begin{aligned} F(t_0,w)&=\int_{-\infty}^{+\infty}f(t)g(t-t_0)e^{iwt}dt\\ F(w)&=\int_{-\infty}^{+\infty}F(t_0,w)dt_0\\ f(t)=\int_{-\infty}^{+\infty}F(w)e^{iwt}dw&=\int_{-\infty}^{+\infty}\int_{-\infty}^{+\infty}F(t_0,w)e^{iwt}dwdt_0 \end{aligned}$

$F(t_0,w)$表示$f(t)在t_0$附近的频率为w的能量（也可以表示为$e^{iwt}$的积分）

那么对$F(t_0,w)$关于$t_0$求积分，很直观的，应该等于$f(t)$在全值域内频率为w的能量大小

这里的$g(t-t_0)$就是窗函数，表示为$f(t)在t_0$附近

但这个窗函数有不足之处，就是窗函数应该是和频率w相关的，因为窗函数划分的是$f(t)$的一个区域，当w很大时，周期就小，那么窗函数划分的区域就应该小；当w很小时，周期很大，那么窗函数划分的区域就应该大。

1.1.6 Morlet(1980)

提出了波函数的形式：

$\psi_{(a,b)}(t)=\frac{1}{\sqrt{(|a|)}}\psi(\frac{t-b}{a})$

详见后文

1.2 傅里叶变换

对f(t)进行傅里叶变换写成：

$\hat{f}(w)=\frac{1}{\sqrt{2\pi}}\int_{-\infty}^{+\infty}f(t)e^{-iwt}dt$

可以理解为向量f(t)在基向量$e^{iwt}$（加负号是为了共轭）上的投影，这个式子表示信号f(t)中包含的频率为$w$的频率成分有多少。

所以这也被称为谱分析，在指定频率那一点有多少能量集中在上面。

也可以理解为一个信号沿着不同的频率给出的能量分布。

1.2.1 傅里叶变换的性质

性质一(帕什瓦尔恒等式Parseval）（能量守恒）：

$\lang f(t),g(t)\rang=\lang\hat{f}(w),\hat{g}(w)\rang$

性质二（向量长度相等）：

$||f||^2=||\hat{f}||^2$

性质三（卷积在傅里叶变换域的表达）：

$\hat{(f*g)}(w)=\hat{f}(w)\hat{g}(w)$

时域中的卷积等于频域中的乘积，这为时域卷积的快速运算提供了理论基础

$(f*g)(t)=\int_{-\infty}^{+\infty}f(u)g(t-u)dt$

上式表示的是f和g的卷积在t这一点的值。则卷积的运算复杂度为$O(N^2)$

1.2.2 傅里叶变换的缺陷

当信号获取时，部分信号发生了漂移。

当信号发生漂移时，需要获取两个信息，漂移的时间和漂移量。

傅里叶变化没有办法处理信号发生漂移的问题。

因为对于基函数$e^{iwt}$，当这个基函数存在时，这个函数会在负无穷到正无穷永远存在，相对于时间来说，频率和频率成分是绝对量，与时间无关。因为范围太广，表示的范围太广太细，以至于会造成两个不同的信号可能有相同的频域图，即容易混淆。

另一方面基函数$e^{iwt}$的能量是无穷大的，详见小波理论及应用_哔哩哔哩_bilibili

1.3 小波（wavelet）

1.3.1 小波定义：

1. $\psi(t)\in L^2(\R)$ (要求基函数必须在想要表达的空间内)
2. $C_\psi =\int_{-\infty}^{+\infty}\frac{|\hat{\psi}(w)|^2}{|w|}dw<+\infty$

称$\Psi(t)$是一个小波母函数

将$\forall a\neq 0,b\in \R,\psi_{(a,b)}(t)=\frac{1}{\sqrt{(|a|)}}\psi(\frac{t-b}{a})$称为依赖参数a，b的连续小波、

其中a为尺度参数，b为唯一参数

1.3.2 小波特征

1.3.2.1 衰减特征

$\int_{-\infty}^{+\infty}|\psi(t)|^2dt<+\infty\\ \int_{-\infty}^{+\infty}|\psi_{(a,b)}(t)|^2dt<+\infty$

即小波会在偏离原点后不断衰减，而不是像$e^{iwt}$那样遍布整个空间

1.3.2.2 波动特征

$\int_{-\infty}^{+\infty}\psi(t)dt=0\\ \int_{-\infty}^{+\infty}\psi_{(a,b)}(t)dt=0$

3

（未完待续）