一、传统目标检测

目标检测（Object Detection) 是一种基于目标几何和统计特征的图像分割，它将目标的分割和识别合二为一。其准确性和实时性是整个系统的一项重要能力。如何平衡准确性和实时性

目标检测任务根据分类问题的性质可以分为两个模块：提取物体区域、对区域进行分类识别。

主要难度： 在提取区域上需要面临不同位置，不同尺寸，提取数量很多的问题。在分类识别方面主要面对CNN分类以及计算量大的问题。

传统的图像目标检测方法流程为：

图像输入—目标候选框选取—特征提取—分类器对候选框判别目标、背景—后处理：非极大值抑制(NMS)—结果输出

1、目标候选框

一个bounding box（边缘框）可以被描述为（左上x，左上y，右下x，右下y）或（左上x，左上y，宽，高）两种。

具体方法有：滑动窗口、选择性搜索、网格搜索、锚点生成、RCNN、Fast RCNN、Faster RCNN

1.1 直接生成候选框的方法

1.1.1 滑动窗口：

形如遍历操作，从左到右、从上到下、不同尺寸的窗口依次遍历输入进分类器。

1.1.2 选择性搜索：

对图像中最有可能包含目标的区域进行搜索以提高效率，首先将输入图像分割成特定数目的小区域，根据这些小区域的相似性（颜色、纹理、大小等）采用子区域合并的方法进行区域迭代合并，生成外切矩形，也就是候选框。选择性搜索既提高了运算效率，又可以包含各种大小的候选框。
(类似图像处理的区域生成法)

1.1.3 ：

其余详见RCNN、Fast RCNN
pass

1.2 基于锚框的方法

1. 提出多个被称为锚框的区域（边缘框）
2. 预测每个锚框里是否含有关注的物体
3. 如果是，预测从这个锚框到真是边缘框的偏移

1.2.1 IoU交并比

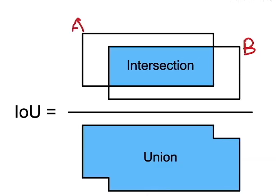
用于计算两个框之间的相似度

1.2.2 赋予锚框标号

1. 每个锚框都是一个训练样本
2. 将每个锚框标注为背景或关联上一个真实边缘框
3. 可能会生成大量的锚框：导致大量的负类样本

实际操作：

2、特征提取的方法有：

harr特征、SIFT特征、LBP特征、Edgelet特征、HOG特征、融合特征

在深度学习之前，最被关注的是特征是怎么样提取的，所以提出了特征算子、视觉词袋（聚类）（？）等方法

2.1 Haar特征（1998、？）：

Haar特征与级联分类器Adaboost方法结合使用

2.1.1 Haar特征概述

在Haar-like特征提出之前，传统的人脸检测算法一般是基于图像像素值进行的，计算量较大且实时性较差。Papageorgiou等人最早将Harr小波用于人脸特征表示，Viola和Jones则在此基础上，提出了多种形式的Haar特征。Lienhart等人对Haar矩形特征做了进一步的扩展，加入了旋转45°的矩形特征，因此现有的Haar特征模板主要如下图所示：

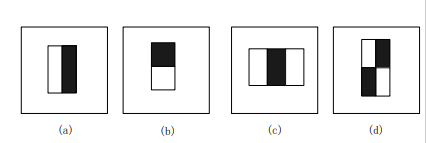
Haar特征分为：边缘特征、线性特征、中心特征和对角线特征，组合成特征模板。特征模板内有白色和黑色两种矩形，并定义该模板的特征值为白色矩形像素和减去黑色矩形像素和。

对于图中a、b这类特征，特征数值计算公式为 v = Sum白 - Sum黑 ；对于图中c这类特征，计算公式为 v = Sum白 - 2Sum黑*，之所以将黑色区域像素和乘以2，是为了使两种矩形区域中像素数目一致。

Haar特征值反映了图像的灰度变化情况。例如：脸部的一些特征能由矩形特征简单的描述，如：眼睛要比脸颊颜色要深，鼻梁两侧比鼻梁颜色要深，嘴巴比周围颜色要深等。但矩形特征只对一些简单的图形结构，如边缘、线段较敏感，所以只能描述特定走向（水平、垂直、对角）的结构。

图中的特征模板称为“特征原型”；通过改变特征模板的大小和位置，可在图像子窗口中穷举出大量的特征。特征原型在图像子窗口中扩展（平移伸缩）得到的特征称为“矩形特征”；矩形特征的值称为“特征值”。

矩形特征值是矩形模版类别、矩形位置和矩形大小这三个因素的函数。故类别、大小和位置的变化，使得很小的检测窗口含有非常多的矩形特征（如：在24*24像素大小的检测窗口内矩形特征数量可以达到16万个）。
这样就有两个问题需要解决：

1. **如何快速计算那么多的特征？ **

2. 哪些矩形特征才是对分类器分类最有效的？

2.1.2 Haar特征的计算：积分图

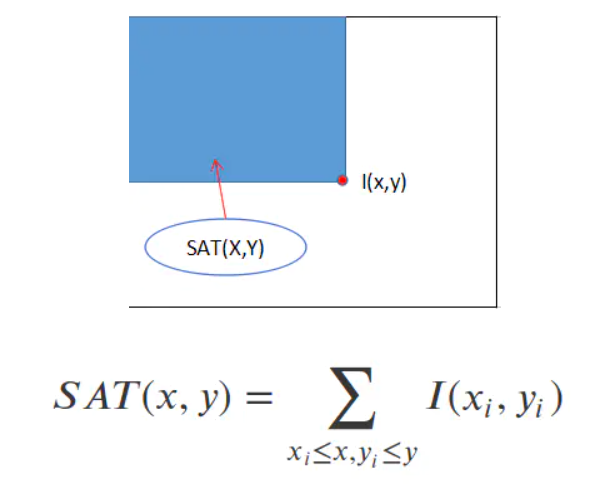
积分图主要的思想是将图像从起点开始到各个点所形成的矩形区域像素之和作为一个数组的元素保存在内存中。
Haar-like 特征积分图的构造方式是位置(i,j)处的值ii(i,j)是原图像(i,j)左上角方向所有像素的和：

$ii(i,j) = \sum_{k\le i, l\le j} f(k,l)$

积分图构建算法：

1. 用s(i,j)表示行方向的累加和，初始化s(i,-1)=0;
2. 用ii(i,j)表示一个积分图像，初始化ii(-1,j)=0；
3. 逐行扫描图像，递归计算每个像素 (i,j) 行方向的累加和s(i,j)和积分图像ii(i,j)的值：

$s(i,j)=s(i,j-1)+f(i,j)$

$ii(i,j)=ii(i-1,j)+s(i,j)$

4. 扫描图像一遍，当到达图像右下角像素时，积分图像ii就构造好了。

积分图构造好之后，图像中任何矩阵区域的像素累加和都可以通过简单运算得到。设D的四个顶点分别为a、b、c、d，则D的像素和可以表示为：

$Sum(D) = ii(a)+ii(b)-(ii(c)+ii(d))$

矩形特征的特征值计算，只与此特征矩形的端点的积分图有关，所以不管此特征矩形的尺度变换如何，特征值的计算所消耗的时间都是常量。这样只要遍历图像一次，就可以求得所有子窗口的特征值。

2.1.3 Haar矩形特征拓展

Lienhart R．等对Haar-like矩形特征库作进一步扩展，加入了旋转45°角的矩形特征。扩展后的特征大致分为4种类型：边缘特征、线特征环、中心环绕特征和对角线特征：

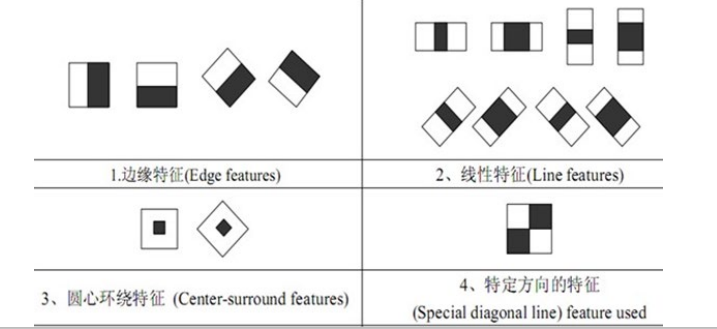
2.2 LBP特征 （1994、？）局部二值模式纹理特征

LBP具有旋转不变性和灰度不变性，即LBP对光照变化是鲁棒的。

2.2.1 LBP特征概述

LBP(Local Binary Pattern，局部二值模式)是一种用来描述图像局部纹理特征的算子，具有旋转不变性和灰度不变性等显著的优点。LBP由T. Ojala，M. Pietikäinen，和D.Harwood在1994年提出，用于纹理特征提取。而且，提取的特征是图像的局部的纹理特征。
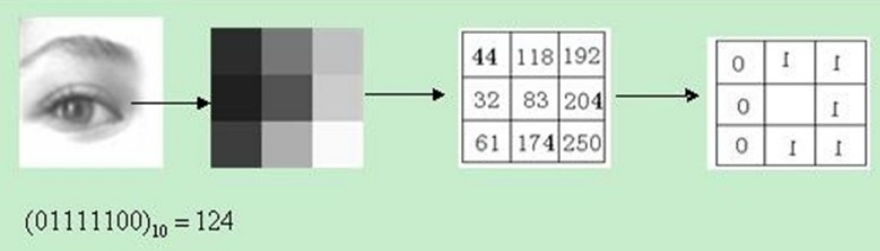
近年来，LBP算子已经得到不断的发展和演化，并广泛地应用于纹理分类、纹理分割、人脸图像分析等领域。 LBP算子定义为在3×3的窗口内，以窗口中心像素为阈值，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3×3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值，并用这个值来反映该区域纹理信息。
图中的二进制代码为在3x3区域内选取特定点作为起点进行的二进制编码，引出之后的LBP不具有旋转不变性以及改进方法

2.2.2 对LBP特征向量进行提取的步骤

1. 首先将检测窗口划分为16×16的小区域(cell)；
2. 对于每个cell中的一个像素，将相邻的8个像素的灰度值与其进行比较，若周围像素值大于中心像素值，则该像素点的位置被标记为1，否则为0。这样，3×3邻域内的8个点经比较可产生8位二进制数，即得到该窗口中心像素点的LBP值；

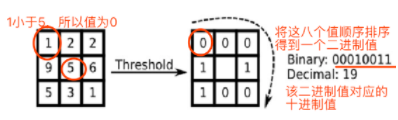
3. 然后计算每个cell的直方图，即每个数字(假定是十进制LBP值)出现的频率；然后对该直方图进行归一化处理;

p为该中间像素依据的邻近像素的个数，$LBP(x_c,y_c)$ = 19为中心点$(x_c,y_c)$的LBP值

4. 最后将得到的每个cell的统计直方图进行连接成为一个特征向量，也就是整幅图的LBP纹理特征向量。

得到了每个像素分割的LBP。建立一个直方图，每个LBP的种类(十进制值)作横轴，每种LBP出现的次数为纵轴。

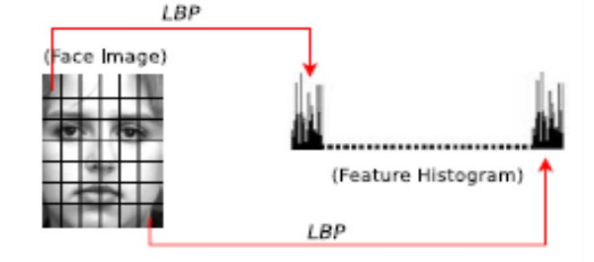
总结：这个方法可以很好地捕捉到图像中的细节，但是固定的近邻区域对于尺寸变化的编码失效。为了适应不同尺度的纹理特征，将3*3的固定领域扩展到了任意领域，并用圆形代替正方形

2.2.3 LBP的改进版本

基本的LBP算子的最大缺陷在于只覆盖了一个固定半径范围内的小区域，这显然不能满足不同尺寸和频率纹理的需要。

1. 圆形LBP算子：
   为了适应不同尺度的纹理特征，并达到灰度不变性的要求，Ojala等对LBP算子进行了改进，将3×3邻域扩展到任意邻域，并用圆形邻域代替了正方形邻域，改进后的LBP算子允许在半径为R的圆形邻域内有任意多个像素点。从而得到了诸如半径为R的圆形区域内含有P个采样点的LBP算子。
   其基本思想是灰度图像的纹理特征通过灰度的分布来体现。假设L是图像的一个区域，则该区域的纹理特征FL可以通过该区域的灰度分布G来描述，即：

$F_L = G(g_c,g_0,g_1,…… ，g_{P-1})$

其中$g_c$为区域中心点c的灰度值, $g_i$(i=0,1,…,P-1)为P个以中心c为圆心，以R为半径的圆周上的等距离分布的领域像素点灰度值。不同的P，R的取值，对应于不同尺度的LBP算子。

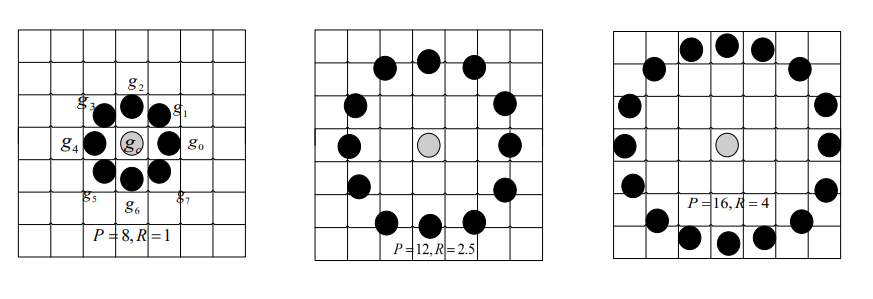
一般来说，当领域采样点个数相同时，半径越小，图像纹理越精细；当半径相同时，领域采样点个数越少，图像亮度越低，区分度变差。如半径都是3的区域，分别划分为4个和8个采样点，4个采样点只有$2^4$种灰度值，区分度肯定没有$2^8$种灰度值的好

当近邻点不在图像的坐标上时，其对应的像素值使用双线性插值算法计算

2. LBP旋转不变模式:
   从LBP的定义可以看出，LBP算子是灰度不变的，但却不是旋转不变的。图像的旋转就会得到不同LBP值。

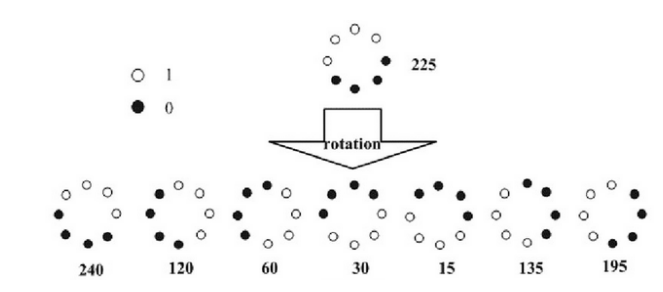
Maenpaa等人又将LBP算子进行了扩展，提出了具有旋转不变性的LBP算子，即不断旋转圆形邻域得到一系列初始定义的LBP值，取其最小值作为该邻域LBP值。

3. LBP等价模式：
   一个LBP算子可以产生不同的二进制模式，对于半径为R的圆形区域内含有P个采样点的LBP算子将会产生$2^P$种模式。很显然，随着邻域集内采样点数的增加，二进制模式的种类是急剧增加的。
   如此多的二值模式无论对于纹理的提取还是对于纹理的表达与识别、分类及信息的存取都是不利的。因此，需要对原始的LBP模式进行降维。
   为了解决二进制模式过多的问题，提高统计性，Ojala提出了采用一种“等价模式”(Uniform Pattern)对LBP算子的模式种类进行降维。
   **Ojala等认为，在实际图像中，绝大多数LBP模式最多只包含两次从1到0或从0到1的跳变。**因此，Ojala将“等价模式”定义为：当某个LBP所对应的循环二进制数从0到1或从1到0最多有两次跳变时，该LBP所对应的二进制就称为一个等价模式类。
   如00000000（0次跳变），00000111（一次跳变），10001111（两次跳变）都是等价模式类。除等价模式类以外的模式都归为另一类，称为混合模式类，例如10010111（四次跳变）。

对于一般的图像，等价模式能占总模式种类比较大的比重。在图(a)，(b)和©中，等价模式占总模式的百分比分别为88%、93％和76％。Ojala指出可以通过低通滤波的方法来增强等价模式所占的比重。如图©，通过高斯滤波后再计算LBP模式，则等价模式所占百分比提高到90%以上。
通过这样的改进，二进制模式的种类大大减少，模式数量由原来的2P种减少为P(P-1)+2种，其中P表示邻域集内的采样点数。
但是，由于图像的千差万别，等价模式并不能在所有的图像中都占到高的百分比，在一些图像中，LBP等价模式所占的比重不足60%，有的甚至更低。而采用低通滤波也有一定的缺陷。

2.2.4 LBPH : LBP特征的统计直方图：

LBPH，Local Binary Patterns Histograms，即LBP特征的统计直方图，LBPH将LBP特征与图像的空间信息结合在一起。

计算该统计直方图的步骤如下：

1. pass

2.3 HOG特征 （2005）方向梯度直方图（和SIFT的区别？）

2.3.1 HOG特征概述

方向梯度直方图（Histogram of Oriented Gradient,HOG）特征通过计算和统计图像局部区域的梯度方向直方图来构成特征。HOG特征结合SVM分类器已经被广泛应用于图像识别中，尤其在行人检测中获得了极大的成功。

1. 主要思想：
   在图像中，局部目标的表象和形状(appearance andshape)能够被梯度或边缘的方向密度分布很好地描述。(本质：梯度的统计信息，而梯度主要存在于边缘的地方)。
2. 具体的实现方法是：
   首先将图像分成小的连通区域，叫做细胞单元。然后采集细胞单元中各像素点的梯度或边缘的方向直方图。最后把这些直方图组合起来就可以构成特征描述器。
3. 优点:与其他特征描述方法相比，HOG有很多优点。首先，由于HOG是在图像的局部方格单元上操作，所以对图像几何的和光学的形变都能保持很好的不变性，这两种形变只会出现在更大的空间领域上。
   其次，在粗的空域抽样、精细的方向抽样以及较强的局部光学归一化等条件下，只要行人大体上能够保持直立的姿势，可以容许行人有一些细微的肢体动作，这些细微的动作可以被忽略而不影响检测效果。因此HOG特征是特别适合于做图像中的人体检测的。

2.3.2 HOG特征提取算法的实现过程：

将一个图像(要检测的目标或者扫描窗口)，做如下操作：

1. 灰度化(将图像看做一个x,y,z(灰度)三维图像)；
2. 采用Gamma校正法对输入图像调节对比度，降低图像局部的阴影和光照变化所造成的影响，同时可以抑制噪声的干扰；
3. 计算图像每个像素的梯度(包括大小和方向)；主要是为了捕获轮廓信息，同时进一步弱化光照的干扰。
4. 将图像划分成小cells(例如6×6像素/cell)；
5. 统计每个cell的梯度直方图(不同梯度的个数)，即可形成每个cell的descriptor；
6. 将每几个cell组成一个block(例如3×3个cell/block)，一个block内所有cell的特征descriptor串联起来便得到该block的HOG特征描述。
7. 将图像内所有block的HOG特征描述串联起来就可以得到该图像(待检测的目标)的HOG特征描述了。这个就是最终的可供分类使用的特征向量了。

具体实现如下：

1. 标准化Gamma空间和颜色空间：
   为了减少光照因素的影响，首先需要将整个图像进行规范化(归一化)。在图像的纹理强度中，局部的表层曝光贡献的比重较大，所以，这种压缩处理能够有效地降低图像局部的阴影和光照变化。因为颜色信息作用不大，通常先转化为灰度图；
   Gamma压缩公式：

$I(x,y) = I(x,y)^{gamma}$

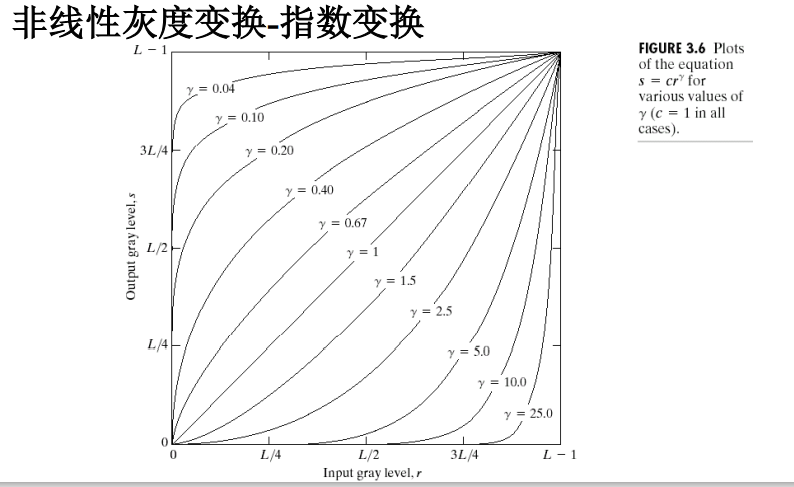
2. 计算图像梯度:
   计算图像横坐标和纵坐标方向的梯度，并据此计算每个像素位置的梯度方向值；求梯度操作不仅能够捕获轮廓，人影和一些纹理信息，还能进一步弱化光照的影响。
   图像中像素点(x,y)的梯度为：

$G_x(x,y) = H(x+1,y) - H(x-1,y)$

$G_y(x,y) = H(x,y+1) - H(x,y-1)$

式中$G_x(x,y)$,$G_y(x,y)$,$H(x,y)$ 分别表示输入图像中像素点(x,y)处的水平方向梯度、垂直方向梯度和像素值。像素点(x,y)处的梯度幅值和梯度方向分别为:

$G(x,y) = \sqrt {G_x(x,y)^2 + G_y(x,y)^2}$

$\alpha (x,y) = \tan ^{-1}(\frac {G_y(x,y)}{G_x(x,y)})$

最常用的方法是：首先用[-1,0,1]梯度算子对原图像做卷积运算，得到x方向(水平方向，以向右为正方向)的梯度分量gradscalx($G_x(x,y)$)，然后用[1,0,-1]T梯度算子对原图像做卷积运算，得到y方向(竖直方向，以向上为正方向)的梯度分量gradscaly($G_y(x,y))$。然后再用以上公式计算该像素点的梯度大小和方向。

3. 为每个细胞单元构建梯度方向直方图
   第三步的目的是为局部图像区域提供一个编码，同时能够保持对图像中人体对象的姿势和外观的弱敏感性。
   将图像分成若干个“单元格cell”，例如每个cell为6×6个像素。假设我们采用9个bin的直方图来统计这6×6个像素的梯度信息。也就是将cell的梯度方向360度分成9个方向块，如图所示：如果这个像素的梯度方向是20-40度，直方图第2个bin的计数就加一，这样对cell内每个像素用梯度方向在直方图中进行加权投影(映射到固定的角度范围)，就可以得到这个cell的梯度方向直方图，就是该cell对应的9维特征向量。

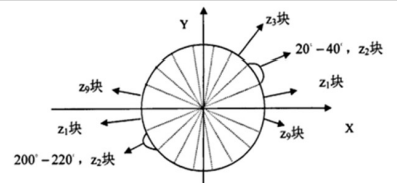
4. 把细胞单元组合成大的块(block)，块内归一化梯度直方图。
   由于局部光照的变化以及前景-背景对比度的变化，使得梯度强度的变化范围非常大。这就需要对梯度强度做归一化。归一化能够进一步地对光照、阴影和边缘进行压缩。
   论文作者采取的办法是：把各个细胞单元组合成大的、空间上连通的区间(blocks)。这样，一个block内所有cell的特征向量串联起来便得到该block的HOG特征。这些区间是互有重叠的，这就意味着：每一个单元格的特征会以不同的结果多次出现在最后的特征向量中。我们将归一化之后的块描述符(向量)就称之为HOG描述符。
5. 收集HOG特征
   最后一步就是将检测窗口中所有重叠的块block进行HOG特征的收集，并将它们结合成最终的特征向量供分类使用。
6. 一个图像的HOG特征维数
   Dalal提出的HOG特征提取的过程：把样本图像分割为若干个像素的单元(cell)，把梯度方向平均划分为9个区间(bin)，在每个单元里面对所有像素的梯度方向在各个方向区间进行直方图统计，得到一个9维的特征向量，每相邻的4个单元构成一个块(block)，把一个块内的特征向量联起来得到36维的特征向量，用块对样本图像进行扫描，扫描步长为一个单元。最后将所有块的特征串联起来，就得到了人体的特征
7. 计算实例：
   对于64 X 128的图像而言，每16 X 16的像素组成一个cell，每2 X 2个cell组成一个块，因为每个cell有9个特征，所以每个块内有4 X 9=36个特征，以8个像素为步长，那么水平方向将有7个扫描窗口，垂直方向将有15个扫描窗口。也就是说，64 X 128的图片，共有36 X 7 X 15=3780个特征。

2.4 SIFT（1999、2004）尺度不变特征变换

SIFT图像匹配及其python实现 - 知乎 (zhihu.com)

SITF算法，即尺度不变特征变换(Scale-invariant feature transform)算法，是由David G.Lowe于1999年提出，并在2004年加以完善。

与图像配准有关（？）

2.4.1 概述

SIFT具有缩放、平移、旋转不变性，对照明变化和仿射或三维投影保持部分不变。

基于SIFT的目标识别方法可以鲁棒的识别出杂乱和遮挡的物体。【文献：Distinctive Image Features from Scale-Invariant Keypoints】

SIFT的思想是将图像数据转换为相对于局部特征的尺度不变坐标

2.4.2 实现步骤

1. 尺度空间极值检测：

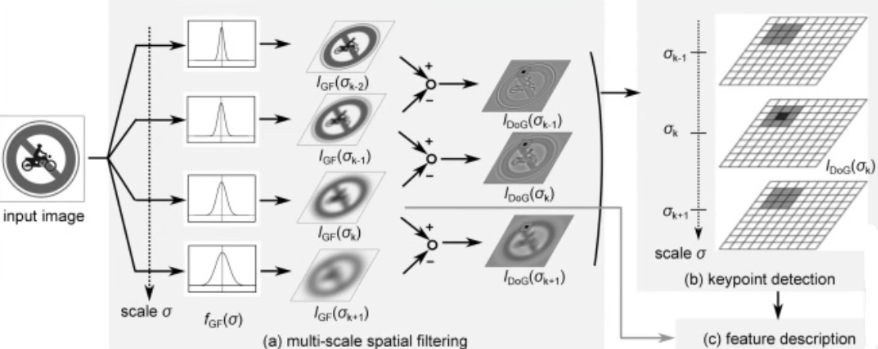
   1. 第一步是搜索所有比例和图像位置。通过使用高斯函数的差分来识别对尺度和方向不变的潜在兴趣点

   2. 使用级联过滤方法检测关键点，该方法使用高效算法来识别候选位置，然后进一步详细检查。关键点检测的第一阶段是识别在同一对象的不同视图下可重复分配的位置和比例。通过使用称为尺度空间的连续尺度函数，在所有可能的尺度上搜索稳定的特征，可以实现对图像尺度变化不变的位置的检测.

      已经被证明的是，唯一可能的尺度空间核是高斯函数，因此，图像的尺度空间被定义为一个函数L（x，y，σ），由可变尺度高斯G（x，y，σ）与输入图像I（x，y）的卷积产生：

      $L(x,y,\sigma)=G(x,y,\sigma)*I(x,y)$

      其中*表示在x和y方向上的卷积,$\sigma$表示高斯卷积核的参数。使用高斯模糊对图像进行高斯平滑且降低图像细节，对图像进行2x2降采样处理，即图像长宽都降低为原来的一半，如此实现图像尺度的降低。

      $G(x,y,\sigma)=\frac{1}{2\pi\sigma^2}e^{-(x^2+y^2)/2\sigma^2}$

   3. DOG尺度空间的构建

      为了检测稳定特征点的位置，SIFT算法用DOG尺度空间来代替尺度空间函数 $L(x,y,\sigma)$。通过对两幅相邻高斯尺度空间图像相减，得到DOG尺度空间。用$D(x,y,\sigma)$函数来表示DOG空间，则该尺度空间的计算公式如下：

      $D(x,y,\sigma)=(G(x,y,k\sigma)-G(x,y,\sigma))*I(x,y)=L(x,y,k\sigma)-L(x,y,\sigma)$

      通过上式也可以看出 DOG 尺度空间中的图像可以反映图像像素的变化，有变化的地方才有特征的存在，因此利用DOG尺度空间来定位特征点。

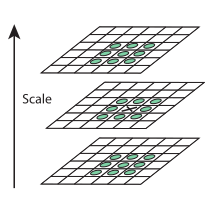
   4. 高斯金字塔

      

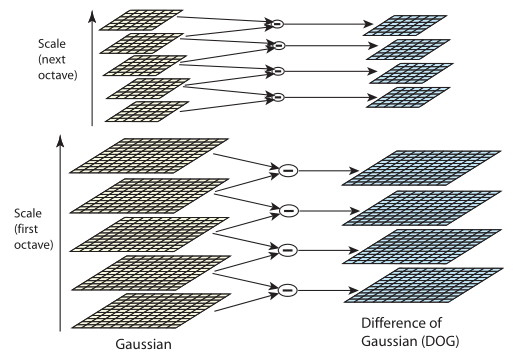
      图中左侧是高斯金字塔，金字塔的每一层是图片进行不同尺度的高斯模糊的结果，每一层中的不同层是高斯卷积核不同的结果，也就是说$\sigma$不同（$\sigma$的不同是通过k来控制的）。

      图中右侧是DOG空间，通过相邻层之间的差分得到的。

2. 关键点定位：

   尺度空间中的所有检测点都与其同尺度相邻的8个点和上下尺度各相邻的9个点进行比较，只保留局部极值点。之后去除其中不好的关键点，通过子像元插值和剔除对比度低的点以及不稳定的边缘响应点来对精化检测到的关键点。

   

   对特征点进行子像元插值，是因为特征点的寻找是在离散空间中进行，找的特征点也是离散的，但是对于连续空间来说，离散的极值点不一定就是函数的最终极值点，所以需要用插值来找到真正的极值点。

   寻找到的极值点并不是图像特征点的另一种情况是，极值点过小。如果极值点与周围像素点差距过小的话，则该极值点是无效极值点。这个点与周围点的差别不是很大，很容易受到噪声的影响，所以对这类点的剔除方法是设定阈值，若检测到的极值点没有超过阈值，则把该极值点去除掉。

   边缘响应较强的点就是横跨边缘处有较大的主曲率且垂直边缘处有较小主曲率的点，首先边缘上的点容易出现二义性，不能确定到底属于哪一个区域，其次易受噪声影响而变得不稳定，所以边缘响应的点一定要去除掉。

   主曲率可以用Hessian矩阵H表示：

   Hessian 就是描述的一个点周围像素梯度大小的变化率，其极值就是生成图像稳定的边缘点（突变点），其两个特征值，代表这其在两个相互垂直方向是的梯度的变化率，当两个特征值越大时，其图像中的像素点的像素值波动越大。我们用两个特征值相加即 Hessian的判别式（即行列式的值）来量化。

   

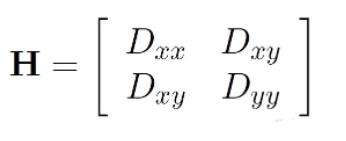
   H的特征值与主曲率成正比，主曲率的变化公式如下：设$\alpha$和$\beta$是H的特征值，$r=\alpha /\beta$，其中$\alpha>\beta$。则

   $T=D_{xx}+D_{yy}=\alpha+\beta$

   $Det=D_{xx}D_{yy}-((D_{xy})^2)=\alpha \beta$

   $\frac{T^2}{Det}=\frac{(\alpha+\beta)^2}{\alpha \beta}=\frac{(r\beta+\beta)^2}{r\beta^2}=\frac{(r+1)^2}{r}$

   通过计算特征值的比率来表示主曲率的变化。如果要去除边缘响应点的话，就需要垂直和横跨边缘方向上差别不是很大的点，如果差别很大的话，则说明是边缘响应点。因此要求 小于一定值。因为r为1时，$\frac{(r+1)^2}{r}$最小，当$r$增加时，$\frac{(r+1)^2}{r}$也会增大，所以只要控制 $r$小于阈值，这样$\frac{(r+1)^2}{r}$会小于一定阈值，$T^2/Det$ 也会小于一定的阈值，那么两个方向上的主曲率差别不大，就去除了边缘响应点。

   因此，可以将满足以下公式的特征点保留，否则剔除掉。

   $\frac{T^2}{Det}<\frac{(r+1)^2}{r}$

   示例：

   

3. 定向作业（方向赋值）：

   特征描述子包含了该描述子所在的尺度、描述子的位置以及描述子的方向。因此生成特征点描述子需要求出描述子的这三个值。尺度是已知的，这里主要说明如何求关键点的方向信息。因为关键点还要满足尺度不变性以及一定的光照和视角不变性等，因此在描述关键点描述子的时候，要综合考虑关键点及其周围像素点的信息，这里的像素点应当是会影响关键点信息的像素点，即对关键点描述子生成有贡献的点。

   首先计算的就是关键点和它周围像素点的梯度大小和方向；计算关键点的主方向会用到梯度直方图，直方图会统计出各个方向上的像素点的个数，像素点个数最多的那个方向就是关键点的主方向（一般10度为一柱，共36柱）。之后将坐标轴方向和关键点主方向保持一致，便能够满足旋转不变性。

   

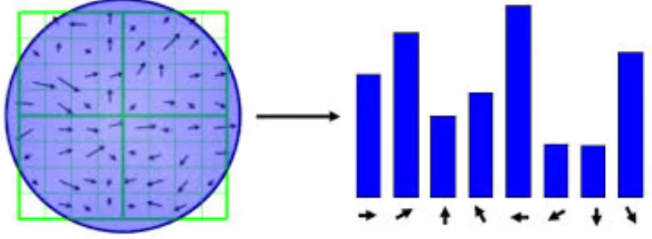
   关键点是圆心，使用一定大小的圆最为窗口来选定关键点周围的像素点。

4. 关键点描述符：

   计算关键点描述子，因为描述关键点不仅与其自身有关，还与它周围的像素点有关，所以将以该特征点为中心的邻域划分成4×4的区域，即特征点周围形成了16个小区域。然后利用梯度直方图统计每个小区域内各方向像素点的个数，那么此区域中与关键点有关的信息就是各个方向的像素点数。因为共有8个方向，且每个方向的像素点数就是一种信息，因此每个区域内会出现8种信息，关键点周围一共形成了4个区域，每个区域8种信息，一共32种信息，而这些信息都要记录在关键点描述子中，所以描述子一共32维。（原文指出最好的结果是使用一个4x4的直方图数组，每个数组中有8个方向箱。因此，本文的实验对每个关键点使用4x4x8=128个元素的特征向量。）

   

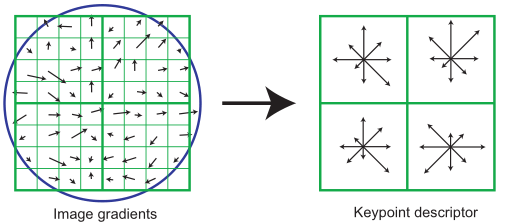
综上，特征点的描述为（x,y,尺度，主方向），特征点的特征为上述的32维

2.4.3 特征点匹配（图像配准）

使用欧氏距离来判断两幅图像特征点的相似性。在匹配过程中，SIFT算法使用的是Kd-tree算法，即找出待配准图像中与参考图像特征点A距离最近的点B和距离次近的点C，则判断特征点A与B是一对匹配点的公式为：

$\frac{d(A,B)}{d(A,C)}<Threshold$

其中d(A,B)为A和距离A最近的点B之间的距离，d(A,C)为A和距离A次近的点C之间的距离。

之后用**RANSAC算法（？）**消除错误匹配点，至此SIFT特征点提取和匹配工作已经完成。

2.4.4 SURF算法（2008）

SURF（Speeded-Up Robust Features）加速稳健特征，是一种稳健的局部特征点检测和描述算法。最初由Herbert Bay发表在2006年的欧洲计算机视觉国际会议ECCV上，并在2008年正式发表在Computer Vision and Image Understanding期刊上。
Surf是可以说是对Sift算法的改进，该算子在保持 SIFT 算子优良性能特点的基础上，同时解决了 SIFT 计算复杂度高、耗时长的缺点，提升了算法的执行效率，为算法在实时计算机视觉系统中应用提供了可能，sift在一般的计算机对于日常使用的图片想做到实时基本上是不可能的。

基本的流程都是一样的，SURF主要有两个关键的优化点：

1. 积分图在Hessian（黑塞矩阵）上的使用：

   解决了运算会重复使用高斯函数对子层进行平滑处理的问题

2. 降维的特征描述子的使用**（harr小波特征？）**

   采用的是统计特征点圆形邻域内的harr小波特征。即在特征点的圆形邻域内，统计60度扇形内所有点的水平、垂直harr小波特征总和，然后扇形以0.2弧度大小的间隔进行旋转并再次统计该区域内harr小波特征值之后，最后将值最大的那个扇形的方向作为该特征点的主方向。该过程示意图如下：

   

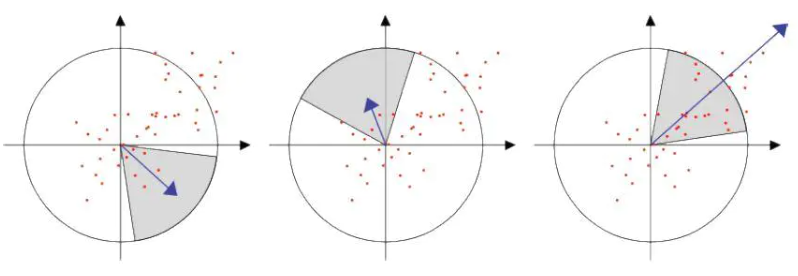
   这样做的有点就是统计的方向更加精确，但是计算时间会略有上升，但是毕竟计算的只有关键点，可忽略不计。

2.5 最大稳定极值区域（MSER）（2002、2011）

最大稳定极值区域（MSER）检测_zizi7的博客-CSDN博客_mser算法

Lowe和Bay提出的SIFT和SURF算法高效实现了具有尺度和旋转不变性的特征检测，但这些特征不具有仿射不变性。

区域检测针对各种不同形状的图像区域，通过对区域的旋转和尺寸归一化，可以实现仿射不变性。

MSER（Maximally Stable Extrernal Regions）是区域检测中影响最大的算法

MSER基于分水岭的概念：对图像进行二值化，二值化阈值取[0, 255]，这样二值化图像就经历一个从全黑到全白的过程（就像水位不断上升的俯瞰图）。在这个过程中，有些连通区域面积随阈值上升的变化很小，这种区域就叫MSER。

$v(i)=\frac{\mid Q_{i+\Delta}-Q_{i-\Delta}\mid}{\mid Q_i\mid}$，其中Qi表示第i个连通区域的面积，Δ表示微小的阈值变化（注水），当vi小于给定阈值时认为该区域为MSER。

显然，这样检测得到的MSER内部灰度值是小于边界的，想象一副黑色背景白色区域的图片，显然这个区域是检测不到的。因此对原图进行一次MSER检测后需要将其反转，再做一次MSER检测，两次操作又称MSER+和MSER-

补充：特征降维

(1).高维特征：

高维特征集合通常存在以下几方面问题：

1. 大量的特征；
2. 许多与给定任务无关的特征；
3. 许多与类别仅有微弱相关度的特征；
4. 许多对于给定任务冗余的特征，如特征相互之间存在强烈的相关度；
5. 噪声数据等。

(2).特征降维：

特征降维(Feature Dimension Reduction)是从高维特征集合中选出低维特征集合，根据一定的评估准则最优化缩小特征空间的过程，它通常是分类与检测问题的预处理步骤。通过合适的方法对数据进行降维能够减少冗余性，进而减弱“维数灾难”的影响。

特征变换：特征变换是指将原有特征通过某种线性变换得到一种低维的新特征。特征变换虽然能够降低数据的维数，但却使得特征的理解性变差。

特征选择：特征选择方法，它是从原始特征集中，按着某种标准选择出特征子集，实现对数据的降维。特征选择方法并未改变原始特征的信息，还能增加特征的可理解性。

1. 特征变换也被称为特征重参数化。特征变换通过将原始特征空间进行变换，重新生成一个维数更小、各维之间更独立的特征空间。可以按照主成分分析(PCA)、**线性判别分析(LDA\Fisher)**等方法进行特征提取。

2. 目前，特征选择还没有比较统一的数学定义，这是因为特征选择需要和具体的应用背景和研究问题相结合。针对不同的问题如分类、回归等，特征选择可笼统地定义为：在满足一定的准则下，寻找原始特征集中“最好”的某一特征或者某一特征子集。从其定义上，可以看出特征选择的本质是对原始特征进行排序或者加权，使最重要的特征排在前几位（权重很大）。特征选择的目的主要有三个：一是改进分类器的预测性能；二是对特征的生成过程有一个更好的认识；三是减少存储空间的使用和计算费用，提高预测速度。
   特征选择算法的实现一般需要四个要素，分别是：原始样本集、搜索策略、评价函数和终止条件。特征选择算法首先需要输入原始样本、特征维数等信息，然后根据某种搜索策略，寻找候选特征子集，并判断该特征子集是否能使评价函数的性能有所改进，最后与终止条件进行比较，判断是否获得最优解，从而执行下一步的方案。

3、传统目标检测分类器有：

级联分类器Adaboost（常与Haar特征结合）、SVM（常与HOG特征结合）

一般选择核函数来计算高维空间两点之间的相关性，通过核函数的计算形成凸优化问题、以至于获得理论解

3.1 ：

见Pycode/ML2/SVM和Adaboost程序

3.2 ：

pass

4、目标检测后处理：

非极大值抑制(NMS)、Soft_NMS、Softer_NMS

后处理的作用：
不管是one-stage还是two-stage的算法，最终算法都会预测出多个结果。在后处理部分中，需要对这些结果做筛选。

4.1 NMS：

1. 优先选择分类分数较高的结果

2. 跟分类分数高的区域重叠较多的结果，可以视为冗余预测框

4.1.1 NMS步骤：

1. 将算法预测出的所有proposals，按照不同的类别标签分组；
2. 对于每一个类别的所有proposals，记作B，筛选后的proposals集合记作D，执行如下操作:
   a) 选择score最高的proposal，记作M(有效预测对象),加入到D(有效集)中；
   b) 计算剩余的proposals与M之间的Iou(交并比)，若大于阈值$N_t$，则舍弃，否则保留；
   c) 若步骤(b)中得到的所有proposals为空，则跳回步骤（2），否则执行步骤(a)。
3. 经过后处理之后，所有类别保留的有效proposals集合为$S={D_{1}, D_{2}, …, D_{c}}$ ，其中c表示目标类别的数量；

4.2 Soft_NMS:

NMS算法保留score最高的预测框，并将与当前预测框重叠较多的proposals视作冗余，显然，在实际的检测任务中，这种思路有明显的缺点，比如对于稠密物体检测，当同类的两个目标距离较近时，如果使用原生的nms，就会导致其中一个目标不能被召回，为了提高这种情况下目标检测的召回率，Soft-NMS应运而生。对于Faster-RCNN在MS-COCO数据集上的结果，将NMS改成Soft-NMS，mAP提升了1.1%。

4.2.1 Soft_NMS算法思想：

NMS采用“一刀切”的思想，将重叠较多的proposals全部视作冗余，而Soft-NMS，采用了“迂回”战术，它认为重叠较多的proposals也有可能包含有效目标，只不过重叠区域越大可能性越小。参见下图，NMS会将绿色框的score置0，而Soft-NMS会将绿色框的score由0.8下降到0.4

为了建立Iou和score之间的联系，Soft_NMS给出了如下公式：

$s_i = s_ie^{-\frac {iou(M,b_i)^2}{\sigma },\forall b_i \notin D}$

其中D表示所有保留的有效框集合，$b_i$表示待过滤的第i个预测框，$s_i$为第i个预测框对应的分类score。这里使用了高斯函数作为惩罚项，当iou=0时，分类score不变，当0< iou < 1时，分类score会做衰减。以上图为例，绿色框$b_i$和红色框M的iou大于0，经过Soft_NMS后该绿色框的分类score由0.8衰减到0.4，可以推断出，如果图中有第2个绿色框，且其与红色框的重叠区域更大时，那么这个新的绿色框的分类score可能由0.8衰减到0.01。

4.2.2 Soft_NMS伪代码：

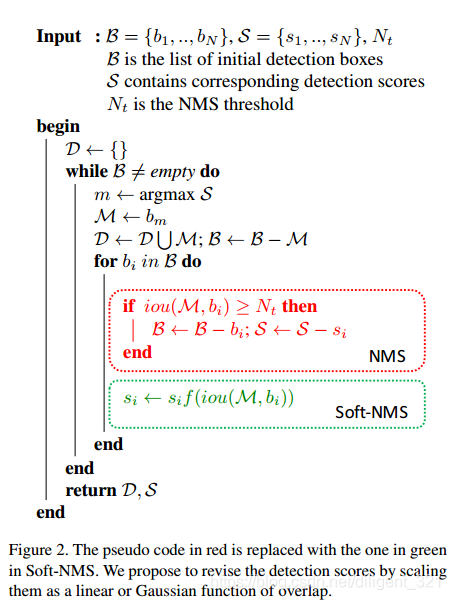
4.3 Softer_NMS:

作者使用VGG-16 faster R-CNN测试了MS-COCO数据集中的图片，论文中贴了两张检测失败的代表图片，如下图：

左图存在的问题：检测出来的2个proposals，沿着y坐标轴方向的定位均不准确；
结论：检测算法预测出来的proposals的坐标不一定准确；
右图存在的问题：检测出来的2个proposals，右边的框分类score较高，但是却沿着x坐标轴方向的定位不准确；
结论：分类score高不一定定位score高，也即classification confidence和 localization confidence不具有一致性。

4.3.1 Softer_NMS的解决方法：

针对上面的问题

1. 既然proposals的坐标不准确，那么即便NMS也无能为力了，所以需要重新设计坐标回归的方式)；
2. 既然分类score高不一定定位score高，那么NMS和Soft-NMS的做法（只基于分类score对proposals做排序）是不准确的，所以需要同时预测出检测框的定位score。

4.3.2 Softer_NMS算法描述：

Softer-NMS的算法框架如下图，可以看出，它跟fast R-CNN是非常相似的，区别在于回归任务中多了一个Box std分支。
Box std的作用是：当预测出的bounding box的坐标为$x_{1}, y_{1}, x_{2}, y_{2} $，该分支会预测出每个坐标的标准差，显然，当坐标的标准差越小时，表明预测得到的坐标值越可信，也即Box std分支用于表征定位任务的置信度。

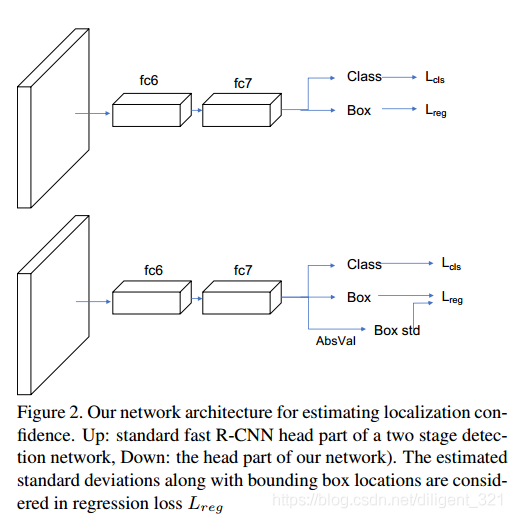
4.3.3 Softer_NMS的定位任务：（？）

在fast R-CNN中，作者使用的是均方误差函数作为定位损失，总的目的是让定位出的坐标点尽可能逼近groundtruth box(GT框，正确标注的框)。本文中为了在定位坐标同时输出定位score，使用了高斯函数建模坐标点的位置分布，公式如下：

$P_\theta (x) = \frac {1}{2\pi \sigma ^2}e^{-\frac {(x-x_e)^2}{2\sigma ^2}}$

其中，$x_e$为预测的box位置,$\sigma$表示box位置的标准差，衡量了box位置的不确定性。

因为groundtruth位置是确定的，所以groundtruth box的坐标为标准差为0的高斯分布，也即Dirac delta函数，公式如下:

$P_D(x) = \delta (x-x_g)$

其中，$x_g$为groundtruth box的坐标。

4.3.4 Softer_NMS的定位损失：

回归任务的目的是让预测框尽可能逼近真实框，也即$P_\theta (x)$和$P_D(x)$为同一分布，衡量概率分布的相似性，自然而然会想到***KL散度（？）(https://hsinjhao.github.io/2019/05/22/KL-DivergenceIntroduction/)***。KL散度本身具有不对称性，通常，在实际应用中为了使用对称性，使用的是KL散度的变形形式，但本文中没有这么做。对公式做化简后，最终的简化形式如下：

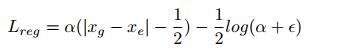
4.3.5 后处理：

经过上面的网络部分，Class分支会输出类别score，Box分支会输出box的4个坐标和这4个坐标对应的标准差（定位score），符号表示如下：

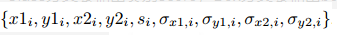
新的后处理算法如下图：

显然，softer-NMS基于回归出的定位confidence，对所有与M的IoU超过阈值$N_t$
的proposals，使用加权平均更新其位置坐标，从而达到提高定位精度的目的。因为softer-NMS关注的是单个框的定位精度，而NMS和soft-NMS关注的是单个框的冗余性，显然关注点不同，所以softer-NMS可以和soft-NMS组合使用，此时效果更佳。

4.4 总结：

NMS：只适用于图片中目标比较稀疏的场景，即目标之间的间距较大；

soft-NMS：可以部分解决出现稠密目标的情况 (ps：Face++提出了RepLoss，从模型的角度解决这一问题，待看)；

softer-NMS：该后处理方法采用"bagging"的思想，通过后处理提高定位精度，可以和soft-NMS组合使用。

二、深度学习概要

在神经网络出现之前，常采用的方法是机器学习和几何学建模方法。

机器学习的步骤是特征提取、选择核函数来计算两个点之间的相关性、转为凸优化问题求解。

优点：具有明确的理论依据。

几何学《Multiple View Geometry-in computer vision》（2000）依赖于对物理模型的假设、具有明确的理论依据、待定

2010年以前计算机视觉最重要的是特征工程从而提出了各种特征算子。

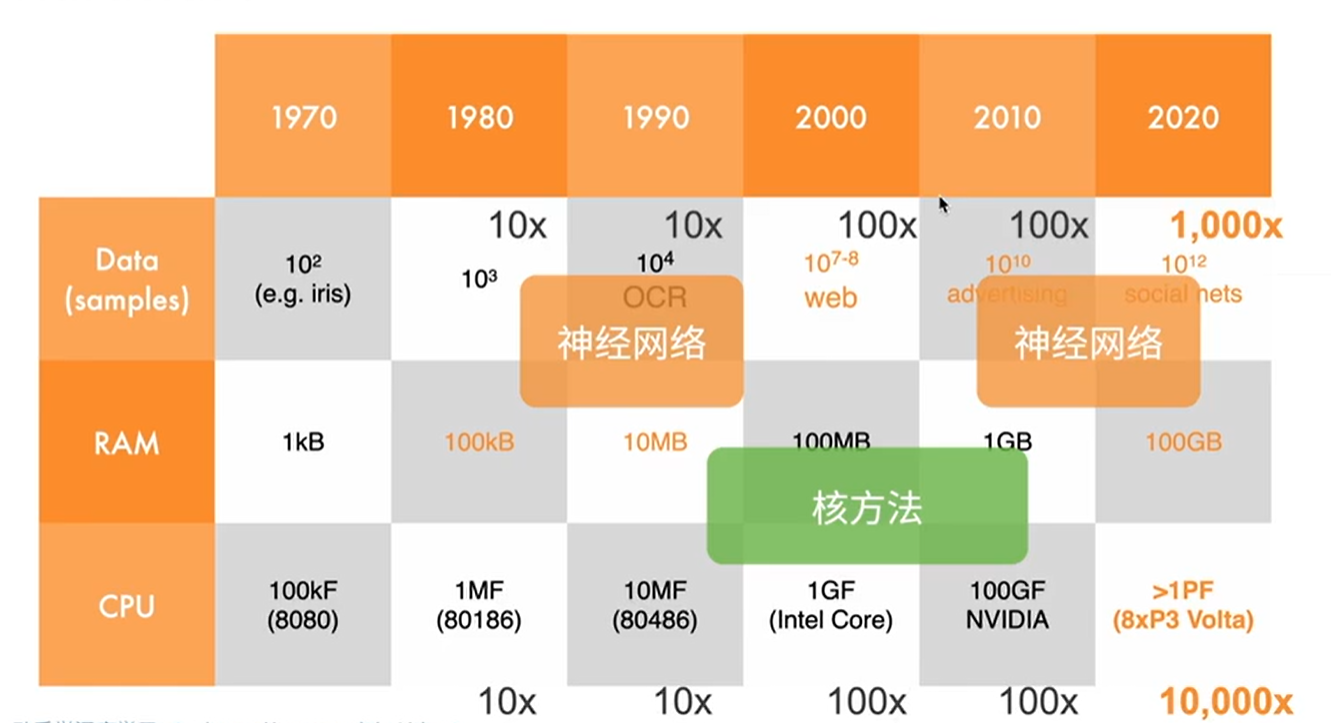
在1990年代，数据量不大情况下，人们采用神经网络模型，因为这个时候的神经网络比较小，计算量比较大、对内存要求不高。

在2000年代，采用核方法，因为核方法简单、具有明确的理论、并且当时的内存和cpu可以运行核方法。

在2010年代，因为内存和cpu性能的提升，可以支持更深层的神经网络，可以挖掘跟深层的数据信息。

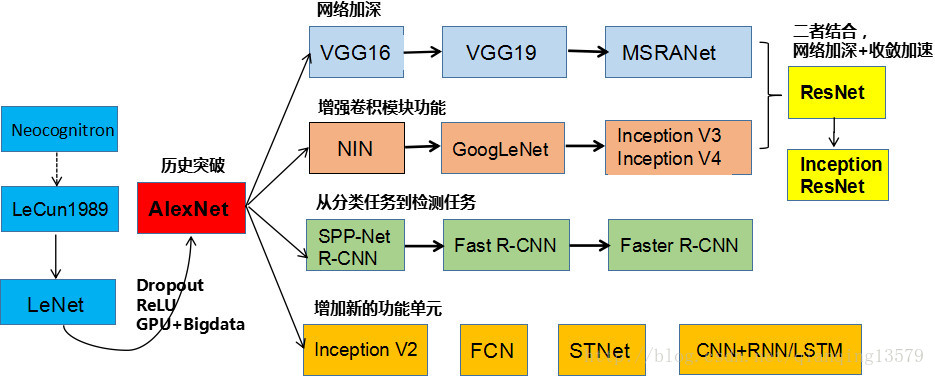
1、卷积神经网络CNN

最基本的CNN原理以及python实现见https://zhuanlan.zhihu.com/p/102119808

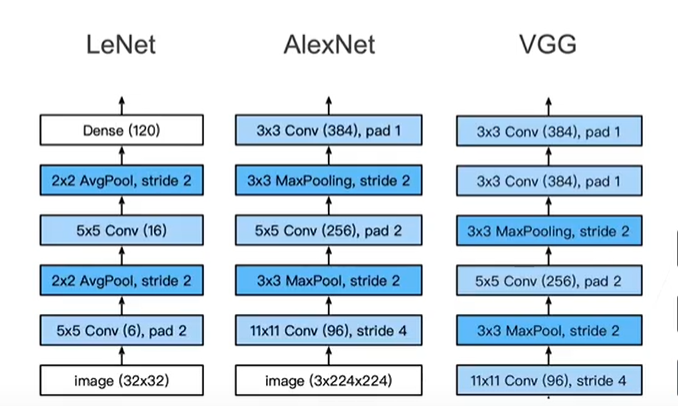
2、 LeNet（1998）

LeNet是最早的卷积神经网络之一。1998年，Yan LeCun第一次将LeNet卷积神经网络应用到图像分类上，在手写数字识别任务中取得了巨大成功。

深入了解见（CNN与LeNet_bebr的博客-CSDN博客_cnn和lenet）

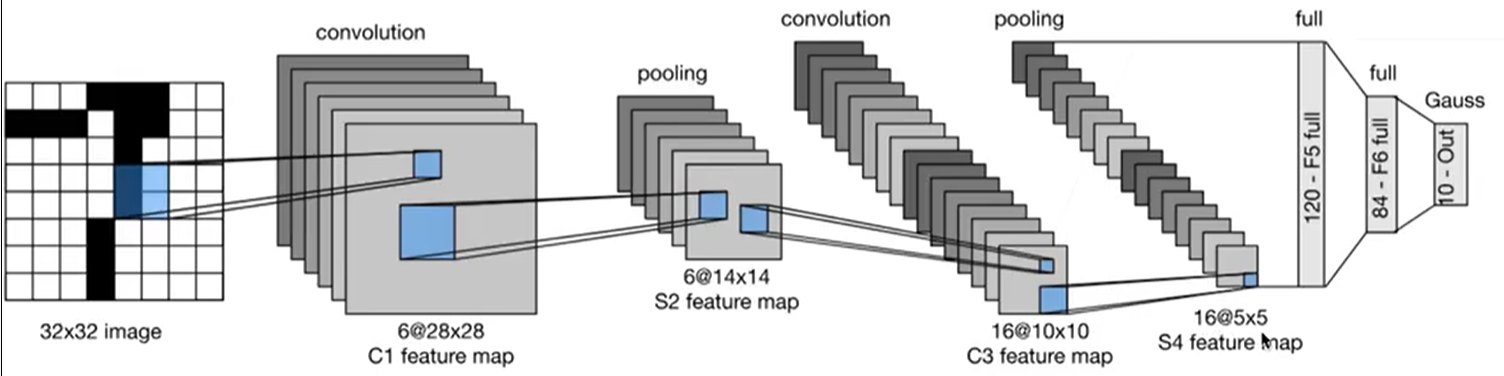
注：通道数的增加是因为采用了不同的卷积核，增加通道数的意义是使一个像素点可以表示多个信息。pooling层是一个下采样操作，增加通道数是提高可能的信息，但总体是一个信息不断减少的系统。

3、 AlexNet（2012）

更深更大的LeNet，量变引起质变，使计算机视觉方法论的改变。

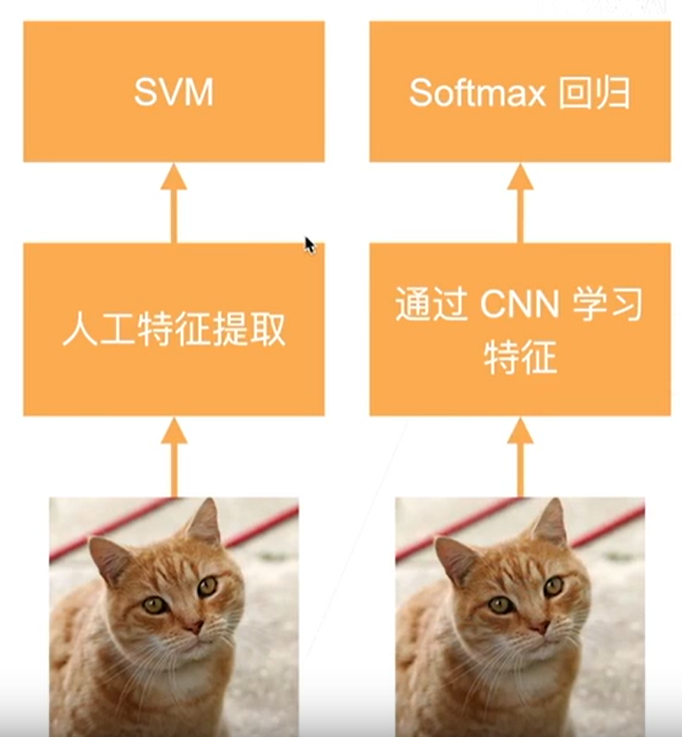
原来的计算机视觉是通过专家对图像的特征进行人工提取，然后交给机器学习模型来分类，这两个步骤是独立的，LeNet模型实际是作为机器学习模型的一种提出的。

AlexNet之后更像是深度学习的模型，让模型自己去学习特征，然后交给softmax回归进行分类，由于这两个步骤是在一个模型中进行训练，所以CNN学习出的特征与softmax回归所需的特征更加吻合，效率更高。这个特性使得深度学习模型是一个端到端模型

3.1 主要改进：

1. DropOut (丢弃法)

2. ReLu

3. MaxPooling （LeNet用的是平均池化）

   最大池化使得输出的差别比较大，使得梯度变大

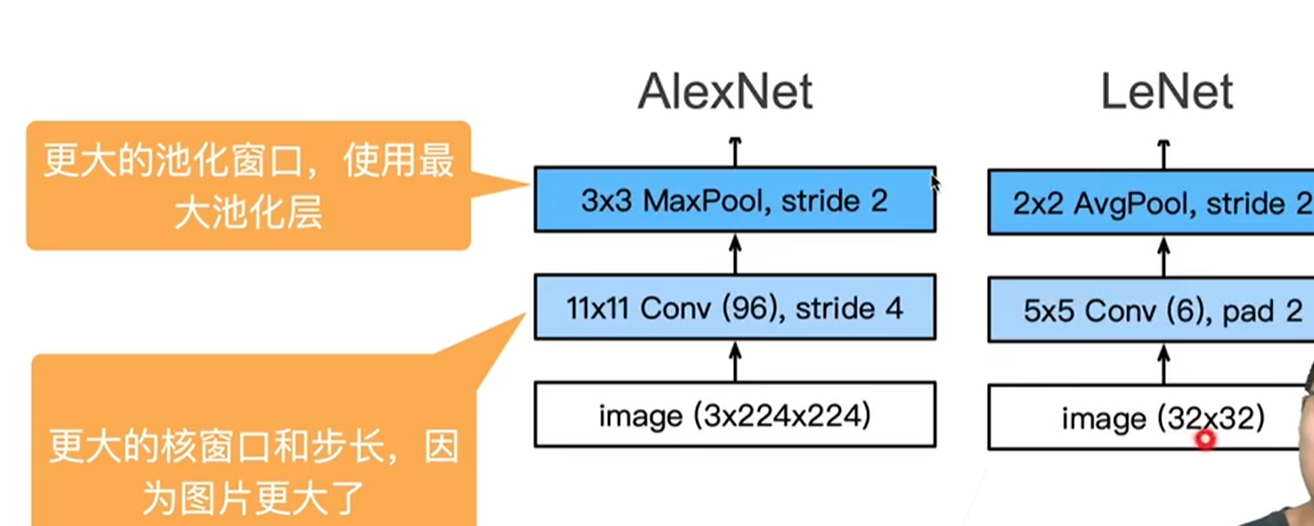
3.2 对比：

1. 输入：AlexNet的输入是更大的RGB图像

2. 卷积：因为图像变大了，所以用更大的卷积窗口去看更大的区域。通道数由6变为96，目的是图像有多个模式，想要在低层次就把它们识别出来。步长为4是降低计算量。

   要识别更多模式就要用更多的通道。

3. 池化：池化窗口的变大使得像素点可移动的范围变大

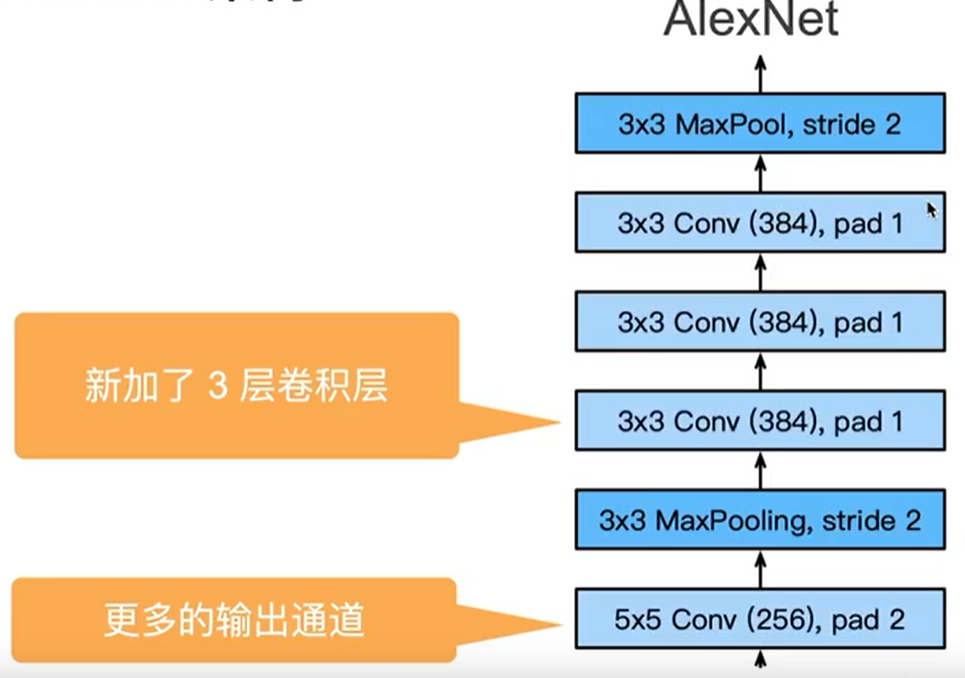
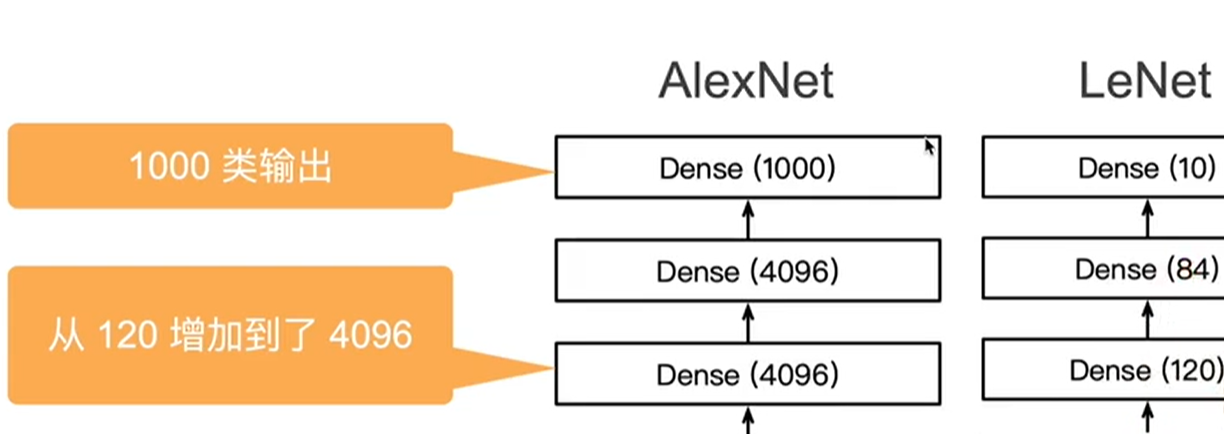
3.3 更多细节：

1. 激活函数从sigmoid变到ReLu（减缓梯度消失）
2. 隐藏全连接层（两个4096）后加入丢弃层dropout
3. 数据增强：不会输入原始图像，而是对原始图像进行颜色、区域的改变后输入。因为卷积对位置、光照敏感。

3.4 复杂度

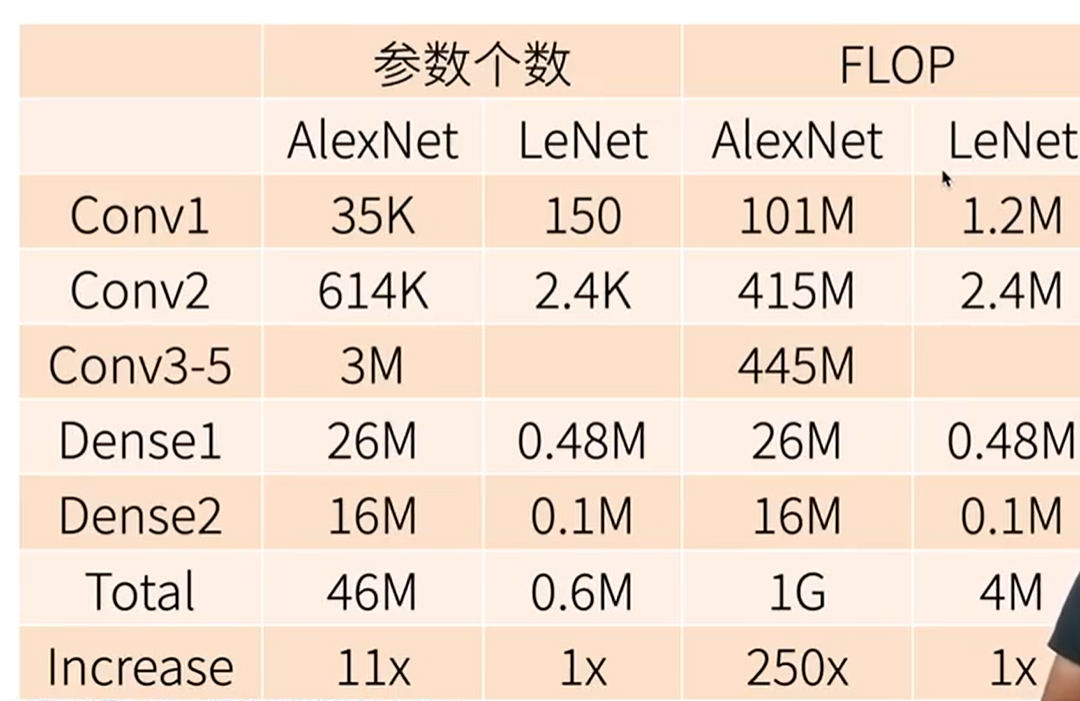
（FLOP浮点数计算量）

3.5 总结

1. AlexNet是更深更大的LeNet，10倍的参数个数，260倍的计算复杂度
2. 提出丢弃法dropout、ReLu、最大池化、数据增强
3. AlexNet是深度神经网络的开端

4、 VGG（块的网络）

AlexNet的结构设计思想不清晰，没有很好的解释为什么要这样设计结构。

考虑到AlexNet提高了层数和规模使得性能比LeNet更好，所以VGG开发者的思路是能不能让网络结构更深更大，从而引出了接下来的三个改进选项：

1. 更多的全连接层：全连接会导致计算量急剧增大，花费高

2. 更多的卷积层：在AlexNet的基础上增加更多的卷积层，但是这样没有太多的实际物理意义

3. 讲卷积层组合层块（VGG块）：码块，AlexNet思路的扩展。

   ​ 一种常用于设计深层神经网络的启发式概念：与芯片设计中工程师从放置晶体管到逻辑元件再到逻辑块的过程类似，神经网络结构的设计也逐渐变得更加抽象。研究人员开始从单个神经元的角度思考问题，发展到整个层次，现在又转向模块，重复各层的模式。

4.1 VGG块

经典卷积神经网络CNN的基本组成部分是下面的这个序列：

1. 带填充以保持分辨率的卷积层
2. 非线性激活函数，如ReLU
3. 池化层

而一个VGG块与之类似，由一系列卷积层组成，后面再加上用于空间下采样的最大池化层。

在最初的VGG论文中，作者使用了带有3x3卷积核，填充为1保持高度和宽度）的卷积层、带有2x2池化窗口、步长为2（每个块后的分辨率减半）的最大池化层。

4.2 VGG网络

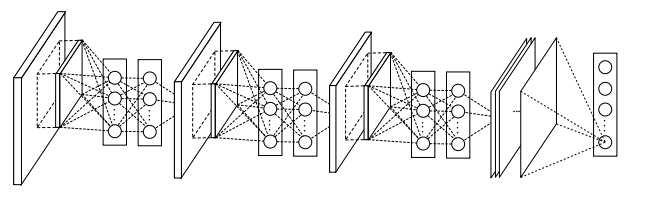
与AlexNet、LeNet一样，VGG网络可以分为两个部分：第一部分主要由卷积层和汇聚层组成，第二部分由全连接层组成。如下图所示：

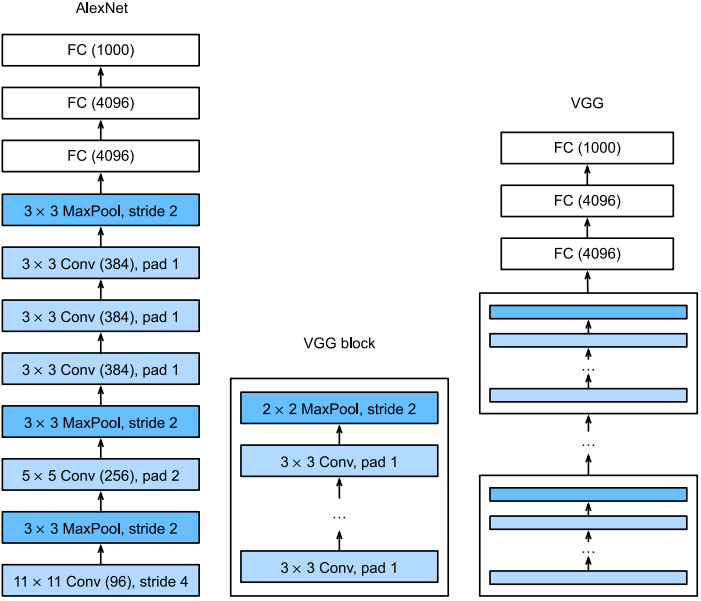
多个VGG块后接全连接层，不同次数的重复块（包括全连接层）得到不同的架构，如VGG-16、VGG-19

Ps：使用3x3而非5x5的卷积核的原因是：试验表明相同计算量下，深但窄的网络比浅但宽的网络更高效

4.3 总结

5、 NiN（网络中的网络）

VGG和AlexNet中存在全连接层的问题：全连接层参数过多的问题，参数过多会占用很高的内存和运算带宽

1. 卷积层的参数个数：输入通道数x输出通道数x窗口的高和宽

   $c_i*c_o*k^2$

2. 卷积层后的第一个全连接层的参数个数：输入通道数x窗口的高和宽x输出的像素个数（通道）

   $c_i*k^2*f_o$

   LeNet 16X5X5X120 = 48K

   AlexNet 256X5X5X4096 = 26M

   VGG 512X7X7X4096 = 102M

5.1 NiN概述

NiN(Network in Network)指的是一个神经网络之中，其每一层之间的特征提取又加上了一个小的神经网络。

NiN目前不常用，但是提出了一些很好的思想，之后的GoogleNet的inception模型的思想就来自NiN。

NiN的两个特点是：

1. 用MLP代替GLM
2. Global Average Pooling（全局平均池化）

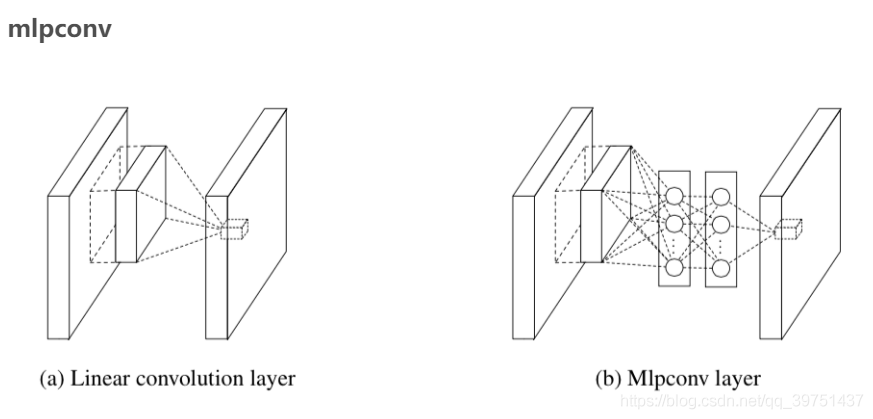
5.1.1 MLP代替GLM (NiN块的结构原理)

GLM是广义线性模型。

MLP是指，在做卷积操作的时候，把线性操作变为多层感知机。（可以看作是加入了两个全连接层，全连接的作用使得线性操作变味了非线性操作）
左图为普通的卷积，右图为mlpconv，mlpconv相当于在正常的卷积层后面，再添加一个1×1的卷积层。

5.1.1.1 NiN块

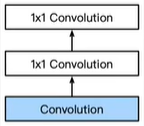
5.1.1.2 1X1卷积核

1×1卷积核最初是在Network in Network这个网络结构中提出来的。它用了比AlexNet更少的参数，达到了跟其一样的效果。

1×1卷积核的作用：

​ 如果当前层和下一层都只有一个通道那么1×1卷积核确实没什么作用，但是如果它们分别为m层和n层的话，1×1卷积核可以起到一个跨通道聚合的作用，所以进一步可以起到降维（或者升维）的作用，起到减少参数的目的。

​ 比如当前层为 x×x×m即图像大小为x×x，特征层数为m，然后如果将其通过1×1的卷积核，特征层数为n，那么只要n<m。这样就能起到降维的目的，减少之后步骤的运算量。如果使用1x1的卷积核，这个操作实现的就是多个feature map的线性组合，可以实现feature map在通道个数上的变化。

​ NIN网络是第一个提出1×1卷积核的论文，同时其也提出了Network in Network的网络概念。因为一般卷积操作可以看成特征的提取操作，而一般卷积一层只相当于一个线性操作，所以其只能提取出线性特征。所以该作者就想能否在卷积层后也加入一个MLP使得每层卷积操作能够提取非线性特征。 其实这里的MLP(多层感知机)，指的是同一层中，不同特征层之间，同一个位置上的值的MLP

5.1.1.3 NiN与1X1卷积核的关系

NiN(Network in Network)指的是一个神经网络之中，其每一层之间的特征提取又加上了一个小的神经网络。

因为NIN中的MLP层可以用两层1×1卷积核来代替，比如当前这一层是54×54×96的图像层，然后过一个1×1×96的卷积核，还是一个54×54×96的卷积层，然后再过一个1×1×96的卷积核，还是一个54×54×96的卷积层。 但是这样但看最开始那个96个特征层的图像同一个位置不同层之间的像素点，相当于过了一个96×96×96的MLP网络 。

5.1.2 Global Average Pooling

Global Average Pooling主要为了解决全连接层参数过多的问题，早期对于分类问题，最后一个卷积层的 Feature Map 通常与全连接层连接，最后通过 softmax 逻辑回归分类。全连接层带来的问题就是参数空间过大，容易过拟合。早期 Alex 采用了Dropout 的方法，来减轻过拟合，提高网络的泛化能力，但依旧无法解决参数过多问题。

而Global Average Pooling的做法是将全连接层去掉，在最后一层，将卷积层设为与类别数目一致，然后全局pooling，从而直接输出各个类别结果。

使用全局平均 pooling 代替全连接层，使得最后一个多层感知卷积层获得的每一个特征图能够对应于一个输出类别，优点如下：

1. 全局平均池化更原生的支持于卷积结构，通过加强特征映射与相应分（种）类的对应关系，特征映射可以很容易地解释为分类映射；
2. 全局平均池化一层没有需要优化的参数，减少大量的训练参数有效避免过拟合；
3. 全局平均池化汇总（求和）空间信息，因此其对空间变换是鲁棒的。

5.2 NiN架构

1. 全程没有全连接层
2. 交替使用NiN块和步幅为2的最大池化层：逐步减小高宽和增大通道数
3. 最后使用全局平均池化层得到输出：其输入通道数就是类别数

5.3 总结

1. 使用NiN块：1X1卷积核对每个像素增加了非线性
2. 使用全局平均池化代替全连接层：不容易过拟合，更少的参数个数

6、 GoogleNet （含并行连结的网络）

考虑前面的几种网络，研究人员提出了这样的疑问：卷积核的大小、步幅、通道数为什么这样选？多大的卷积核是最好的？1X1、3X3、5X5、Max pooling、Average Pooling、MLP怎么选择，用谁比较好？

基于这个疑问，提出了Inception块。

6.1 Inception块

inception（盗梦空间）即为层中层、套娃的意思。

inception的思想是既然不知道上述的方式哪种比较好，那么就都要用。

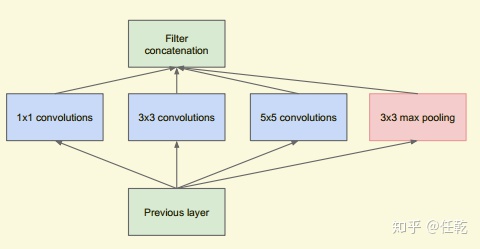
如上图，inception试图根据4个路径从不同层面提取信息，然后在输出通道合并。图中使用了不同大小窗口的卷积层、池化层，然后在输出的concatenation整合成与输入相同大小的输出。

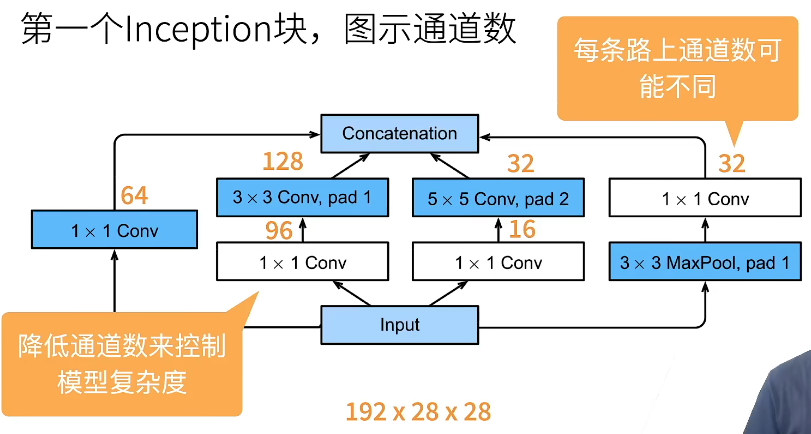
图中标成白色的卷积实际作用可以看作是改变通道数，以降低模型复杂度。1X1 Conv抽取通道信息，剩下三个抽取蓝框抽取空间信息。可以把分配的通道数看作权重，但是这样通道数的划分并没有明确的理论依据，只是大致划分。

优点：

1. 增加了提取信息的多样性
2. 和单3X3或5X5卷积层比，inception块有更少的参数个数和计算复杂度。
3. 不改变高宽，只改变通道数

缺点：

1. 超参过多，过于复杂，对设备要求高，难以复现
2. 严重没有理论支撑，难以理解，过于玄学（深度学习的玄学从这里开始体现的）

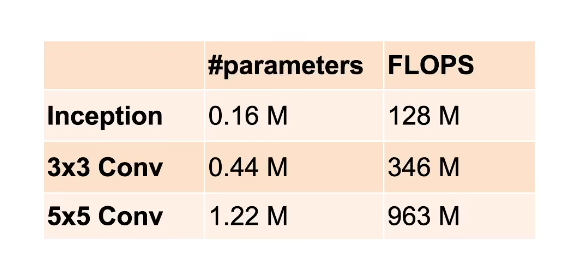
6.2 GoogleNet架构

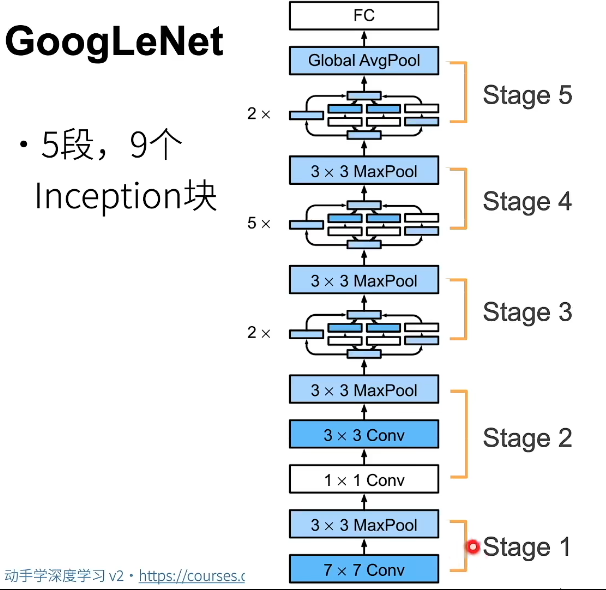
6.2.1 stage1&2

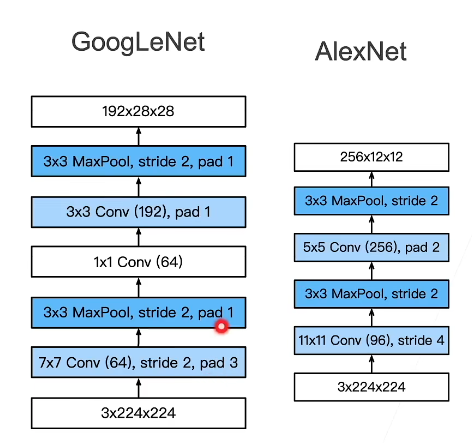
更小的窗口、更多的通道，以至于保留了更多的高宽，可以支撑更深的网络。

6.2.2 stage3

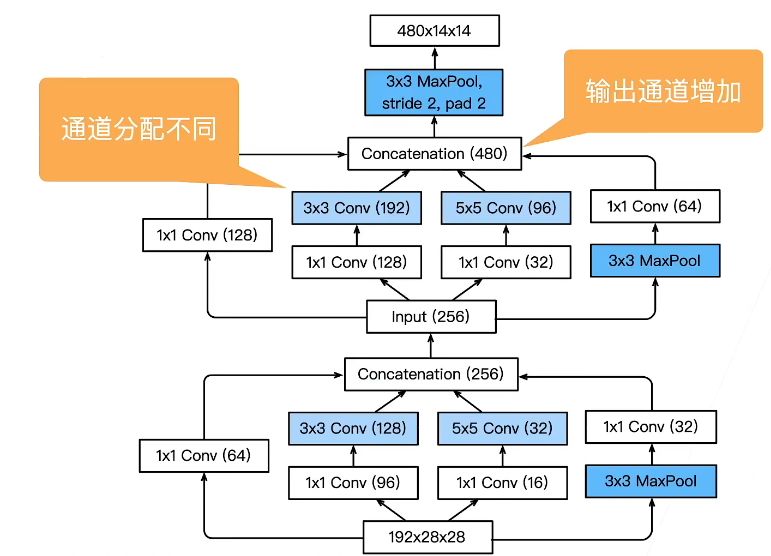
6.3 Inception变种

1. Inception-BN(v2):使用batch normalization
2. Inception-V3:修改Inception块:
   1. 替换5x5为多个3x3卷积层
   2. 替换5x5为1x7和7x1卷积层
   3. 替换3x3为1x3和3x1卷积层，等等
3. Inception-V4：使用残差连接

6.4 总结

1. Inception块用4条有不同超参数的卷积层和池化层的路来抽取不同的信息
   1. 它的一个主要优点是模型参数小，计算复杂度低
2. GoogleNet使用了9个Inception块，是第一个达到上百层的网络(不是纯深度，有一定的宽度)
   1. 后续有一系列改进

7、 批量归一化(Batch Normalization)

7.1 使用批量归一化BN的原因

使用浅层模型时，随着模型训练的进行，当每层中参数更新时，靠近输出层的输出较难出现剧烈变化。对深层神经网络来说，随着网络训练的进行，前一层参数的调整使得后一层输入数据的分布发生变化，各层在训练的过程中就需要不断的改变以适应学习这种新的数据分布。所以即使输入数据已做标准化，训练中模型参数的更新依然很容易导致后面层输入数据分布的变化，只要网络的前面几层发生微小的改变，那么后面几层就会被累积放大下去。最终造成靠近输出层输出的剧烈变化。这种计算数值的不稳定性通常令我们难以训练出有效的深度模型。如果训练过程中，训练数据的分布一直在发生变化，那么将不仅会增大训练的复杂度，影响网络的训练速度而且增加了过拟合的风险。

在模型训练时，在应用激活函数之前，先对一个层的输出进行归一化，将所有批数据强制在统一的数据分布下，然后再将其输入到下一层，使整个神经网络在各层的中间输出的数值更稳定。从而使深层神经网络更容易收敛而且降低模型过拟合的风险。

批量归一化BN的优势：

1. 不加批量归一化的网络需要慢慢的调整学习率时，网络中加入批量归一化时，可以采用初始化很大的学习率，然后学习率衰减速度也很大，因此这个算法收敛很快。
2. BN可以大大提高模型训练速度，提高网络泛化性能。
3. 数据批量归一化后相当于只使用了S型激活函数的线性部分，可以缓解S型激活函数反向传播中的梯度消失的问题。

深层神经网络在做非线性变换前的激活输入值，随着网络深度加深或者在训练过程中，其分布逐渐发生偏移或者变动，整体分布逐渐往非线性函数的取值区间的上下限两端靠近，这会导致反向传播时低层神经网络的梯度消失，BN就是通过一定的规范化手段，把每层神经网络任意神经元这个输入值的分布强行拉回到均值为0方差为1的标准正态分布，使得激活输入值落在非线性函数对输入比较敏感的线性区域，其对应的导数远离导数饱和区 ，这样输入的小变化就会导致损失函数较大的变化，避免梯度消失问题产生，学习收敛速度快，能大大加快训练速度。

7.2 批量归一化BN实现方法

固定小批量B里面的均值和方差：

$均值：\mu _B = \tfrac {1}{\mid B\mid} \sum_{i\in B}x_i$

$方差：\sigma_{B}^{2} = \tfrac{1}{\mid B\mid}\sum_{i\in B}(x_i-\mu_B)^2+\epsilon (很小的数，防止变为0)$

然后再做额外的调整

$x_{i+1}=\gamma \tfrac{x_i-\mu_B}{\sigma_B}+\beta$

$\gamma (方差)和\beta(均值)是可学习参数$，因为考虑到强硬的使分布变为均值为0方差1的分布可能不易于分类，所以加入两个可学习参数让神经网络学习，相当于对均值为0方差1的分布进行一定的缩放和平移，以便更好的分类。

7.3 批量归一化层的定位

1. 具有可学习参数$\gamma (方差)和\beta(均值)$
2. 作用在
   1. 全连接层在卷积层输出上，激活函数前
   2. 全连接层和卷积层输入上
3. 对全连接层，作用在特征维
4. 对于卷积层，作用在通道维：即对单个像素的不同通道计算均值方差（经过卷积操作后，每个像素相当于一个样本，每个像素的通道对应样本的特征，所以说卷积层的通道维相当于全连接层的特征维）

7.4 批量归一化的作用

最初的论文是想用它来减少内部协变量转移，但后续论文指出它可能就是通过在每个小批量里加入了随机噪声来控制模型复杂度

$x_{i+1}=\gamma \tfrac{x_i-\mu_B}{\sigma_B}+\beta$

$\mu_B和\sigma_B$分别是随机偏移和随机缩放，目前的解释可能不对。

因为是加入随机噪声，随意没必要和丢弃法（dropout）混合使用

7.5 总结

1. 批量归一化固定小批量的均值和方差，然后学习出适合的偏移和缩放
2. 可以加快收敛速度，但一般不改变模型精度
3. 把每层的数据固定在差不多的分布里，避免了因为学习率的过大过小引起的梯度爆炸或消失，使网络可以使用统一的学习率来训练

8、 残差网络（ResNet）

残差神经网络的主要贡献是发现了“退化现象（Degradation）”，并针对退化现象发明了 “短路连接（Shortcut connection）”，极大的消除了深度过大的神经网络训练困难问题。神经网络的“深度”首次突破了100层、最大的神经网络甚至超过了1000层。

8.1 退化现象

在之前的LeNet、AlexNet、VGG、GoogleNet模型中，改进的方向都是做的更深更大，但是没有理论证实更深更大的神经网络准确率就一定高吗。

通过实验，随着网络层不断的加深，神经网络模型的准确率先是不断的提高，达到最大值（准确率饱和），然后随着网络深度的继续增加，模型准确率毫无征兆的出现大幅度的降低。

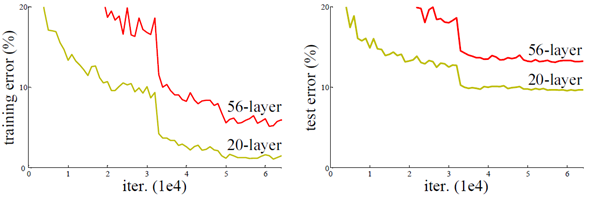
这个现象与“越深的网络准确率越高”的信念显然是矛盾的、冲突的。ResNet团队把这一现象称为“退化（Degradation）”。

ResNet团队把退化现象归因为深层神经网络难以实现“恒等变换（y=x）”。

考虑这样一个事实：现在你有一个浅层网络，你想通过向上堆积新层来建立深层网络，一个极端情况是这些增加的层什么也不学习，仅仅复制浅层网络的特征，即这样新层是恒等映射（Identity mapping）。在这种情况下，深层网络应该至少和浅层网络性能一样，也不应该出现退化现象。

与传统的机器学习相比，深度学习的关键特征在于网络层数更深、非线性转换（激活）、自动的特征提取和特征转换，其中，非线性转换是关键目标，它将数据映射到高纬空间以便于更好的完成“数据分类”。随着网络深度的不断增大，所引入的激活函数也越来越多，数据被映射到更加离散的空间，此时已经难以让数据回到原点（恒等变换）。或者说，神经网络将这些数据映射回原点所需要的计算量，已经远远超过我们所能承受的。

退化现象让我们对非线性转换进行反思，非线性转换极大的提高了数据分类能力，但是，随着网络的深度不断的加大，我们在非线性转换方面已经走的太远，竟然无法实现线性转换。显然，在神经网络中增加线性转换分支成为很好的选择，于是，ResNet团队在ResNet模块中增加了快捷连接分支，在线性转换和非线性转换之间寻求一个平衡。

8.2 ResNet架构

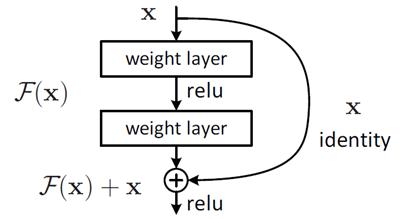
三、深度学习目标检测算法

1、前言

目标检测数据集的每行表示一个物体：图片文件名、物体类别、边缘框

一个bounding box（边缘框）可以被描述为（左上x，左上y，右下x，右下y）或（左上x，左上y，宽，高）两种。

下述算法均是基于锚框的算法

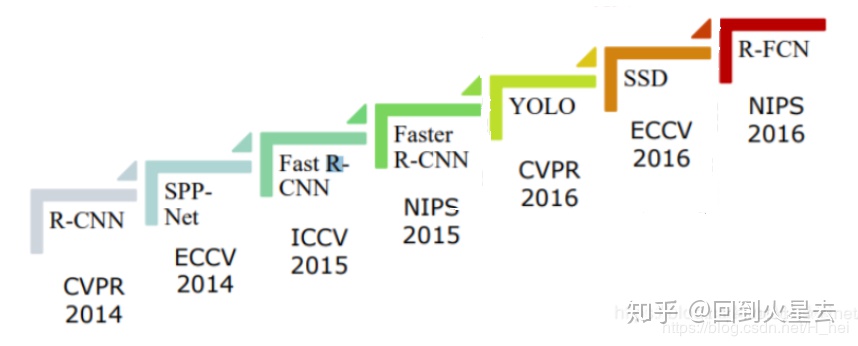
2、Region—CNN（区域卷积神经网络R-CNN）

浅谈深度神经网络 — R-CNN（区域卷积神经网络） - 知乎 (zhihu.com)

R-CNN是第一个成功将深度学习应用到目标检测上的算法。

R-CNN遵循传统目标检测的思路，同样采用提取框，对每个框提取特征、图像分类、 非极大值抑制四个步骤进行目标检测。只不过在提取特征这一步，将传统的特征(如 SIFT、HOG 特征等)换成了深度卷积网络提取的特征。

1. 使用启发式搜索算法来选择锚框
2. 使用预训练模型来对每个锚框抽取特征
3. 训练一个SVM来对类别分类
4. 训练一个线性回归模型来预测边缘框偏移

2.1 R-CNN详细步骤：

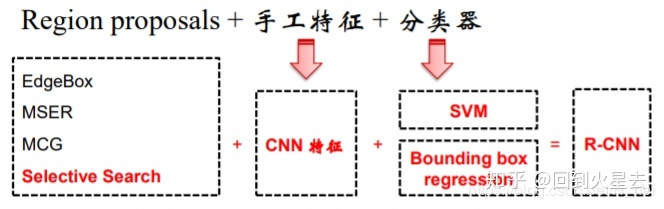
R-CNN的步骤如下：

1. 图像输入
2. 区域建议（Region proposals ？）：选择性搜索
3. 使用CNN进行特征提取。这里需要注意的是区域建议选取的边缘框尺寸大小可能不一样，所以在放入CNN之前需要对选取的边缘框进行缩放处理成统一的227x227的大小。CNN模型借鉴的AlexNet模型，稍有改动。
4. SVM分类：将提取出来的特征送入SVM分类器得到分类模型，在这里每个类别对应一个SVM分类器，如果有20个类别，则会有20SVM分类器。对于每个类别的分类器只需要判断是不是这个类别的，如果同时多个结果为Positive则选择概率之最高的。
5. 边缘框回归（？）
6. 非极大值抑制

2.2 一些问题

R-CNN虽然不再像传统方法那样穷举，但R-CNN流程的第一步中对原始图片通过Selective Search提取的候选框region proposal多达2000个左右，而这2000个候选框每个框都需要进行CNN提特征+SVM分类，计算量很大，导致R-CNN检测速度很慢，一张图都需要47s。

那么有没有方法提速呢？答案是有的，这2000个region proposal不都是图像的一部分吗，那么我们完全可以对图像提一次卷积层特征，然后只需要将region proposal在原图的位置映射到卷积层特征图上，这样对于一张图像我们只需要提一次卷积层特征，然后将每个region proposal的卷积层特征输入到全连接层做后续操作。

但现在的问题是每个region proposal的尺度不一样，而全连接层输入必须是固定的长度，所以直接这样输入全连接层肯定是不行的。SPP Net恰好可以解决这个问题。

3、 SPP-Net（空间金字塔池化）

3.1 模型概述

SPP：Spatial Pyramid Pooling（空间金字塔池化）

CNN一般都含有卷积部分和全连接部分，其中，卷积层不需要固定尺寸的图像，而全连接层是需要固定大小的输入。所以当全连接层面对各种尺寸的输入数据时，就需要对输入数据进行crop（crop就是从一个大图扣出网络输入大小的patch，比如227×227），或warp（把一个边界框bounding box的内容resize成227×227）等一系列操作以统一图片的尺寸大小。

但warp/crop这种预处理，导致的问题要么被拉伸变形、要么物体不全，限制了识别精确度。

既然由于全连接FC层的存在，普通的CNN需要通过固定输入图片的大小来使得全连接层的输入固定。那借鉴卷积层可以适应任何尺寸，为何不能在卷积层的最后加入某种结构，使得后面全连接层得到的输入变成固定的呢？

3.2 兴趣区域（RoI）池化层

考虑到不同锚框的大小可能不一样，所以给定一个锚框，均匀分割成n*m块，输出每块里的最大值

不管锚框多大，总是输出n*m个值

ROI池化层一般跟在卷积层后面，此时网络的输入可以是任意尺度的，在SPP layer中每一个pooling的filter会根据输入调整大小，而SPP的输出则是固定维数的向量，然后给到全连接FC层。

3.3 SPP（空间金字塔池化层）

RoI是SPP的特殊形式

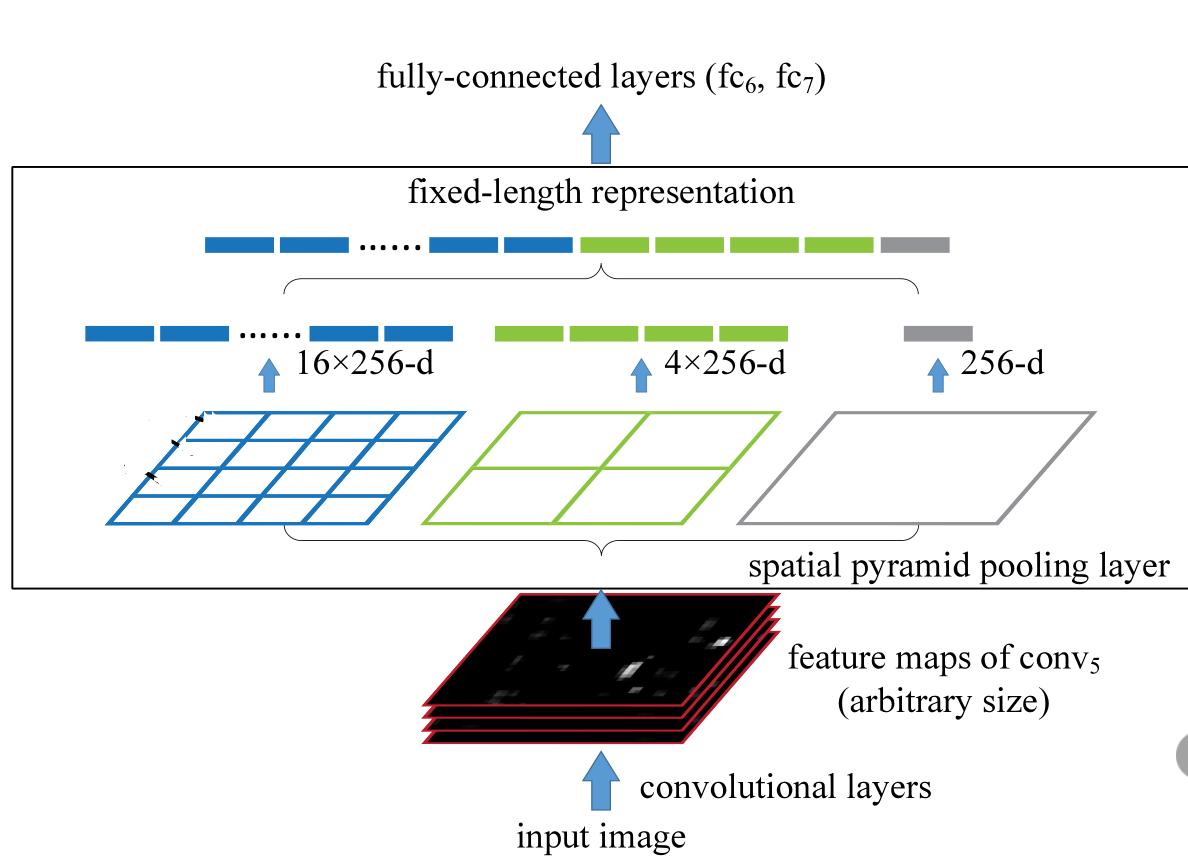
3.4 总结

1. 适应不同输入尺寸：CNN原本只能固定输入、固定输出，CNN加上SSP之后，便能任意输入、固定输出。
2. 问题：需要存储大量特征、复杂的多阶段训练、训练时间长

4、 Fast R-CNN

4.1 改进

1. 共享计算：直接输入整图，所有区域共享卷积计算（一遍），再把候选框映射到conv5上，在CNN输出上提取所有区域的特征。比R-CNN，SPP-Net更快的train/test，更高的准确率，召回率。
2. 实现end-to-end（端对端）单阶段训练，使用多任务损失函数。
3. 所有层都可以fine-tune（再训练，把模型拿过来针对现在要解决问题的数据集再次训练，以更加适应现在数据集。）
4. 不需要离线存储特征文件

4.2 多任务损失函数

pass

5、 Faster R-CNN

使用区域建议网络（RPN，Region proposal network）来替代之前启发式搜索来获得更好的锚框

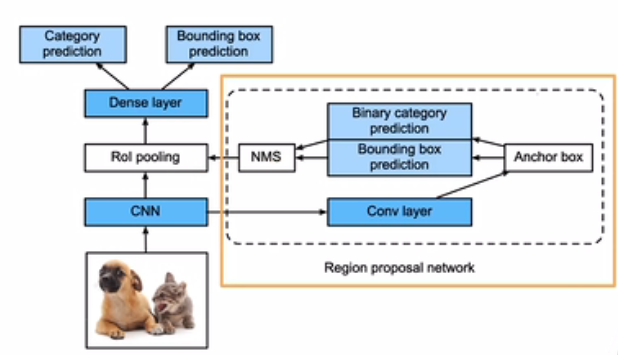
大意为：先在RPN中生成随机（比较粗糙）的锚框进行简单的目标检测，然后选出效果比较好的锚框用于大网络中。

Faster RCNN其实是比较慢的，但精度高（直觉上很好理解）。在进精度要求很高的情况下使用Faster和Mask

6、 Mask R-CNN

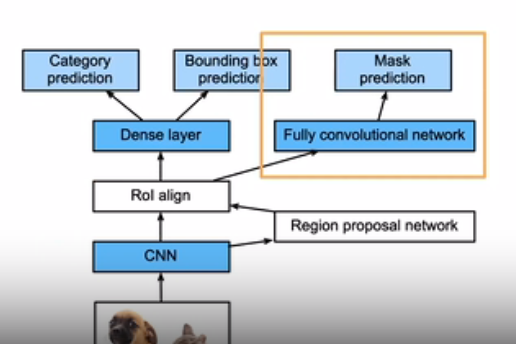
如果有像素级别的标号，使用**FCN（见后续）**来利用这些信息（辅助训练）

对数据集的要求高，在无人车领域用的比较多

7、单发多框检测（SSD）

7.1 锚点生成

对每个像素，生成多个以它为中心的锚框，对这些锚框直接做预测

7.2 框架

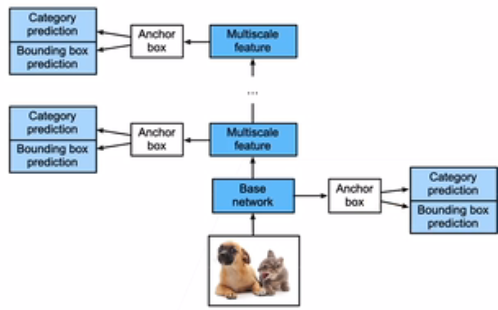
一个基础网络来抽取特征，然后多个卷积层块来减半高宽

在每段都生成锚框：底部段来拟合小物体，顶部段来拟合大物体

对每个锚框预测类别和边缘框

7.3 总结

1. SSD通过单神经网络来检测模型
2. 在多个段的输出上进行多尺度预测
3. SSD的速度快，但精度低（目前没有更新）

8、 YOLO （you only look once）

1. SSD中锚框大量重叠，因此浪费了很多计算
2. YOLO将图片均匀分成S*S个锚框
3. 每个锚框预测B个边缘框（网格搜索）（V1）

V3的一个改进：对数据集进行聚类，预测可能的锚框应该是什么样的（研究数据集中的规律）

四、语义分割

1、转置卷积

1. 卷积不会增大输入的高宽、通常要么不变、要么减半
2. 转置卷积则可以用来增大输入高宽

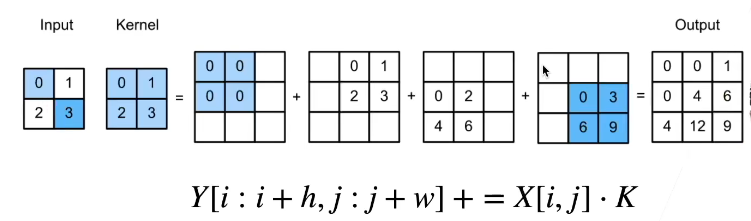
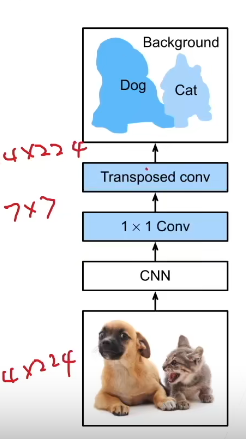
2、全连接卷积神经网络FCN

1. FCN是用深度神经网络来做语义分割的奠基性工具
2. FCN用转置卷积层来替换CNN最后的全连接层，从而可以实现每个像素的预测

五、序列模型

数据具有时序结构

1、统计工具

在时间t观察到$x_t$,那么得到T个不独立的随机变量

$(x_1,...,x_T)~p(x)$

使用条件概率展开

$p(a,b)=p(a)p(b\mid a)=p(b)p(a\mid b)$

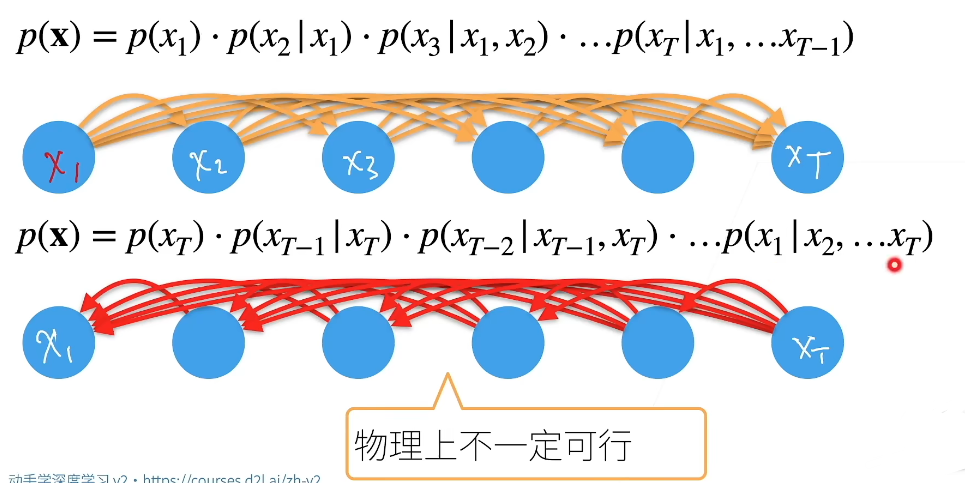
对条件概率建模

$p(x_t\mid x_1,...,x_{t-1})=p(x_t\mid f(x_1,...,x_{t-1}))$

$f(x_1,...,x_{t-1})$的意思是对之前见过的t-1个样本建模来预测第t个样本的值。

$f(x_1,...,x_{t-1})$对见过的数据建模，也称自回归模型

关键就是怎么算f（）

方案1：马尔科夫假设

假设当前数据只跟$\tau$个过去数据点相关

$p(x_t\mid x_1,...,x_{t-1})=p(x_t\mid x_{t-\tau},...,x_{t-1})=p(x_t\mid f(x_{t-\tau},...,x_{t-1}))$

如果给定了定长$\tau$，那么只用对过去$\tau$长度的数据进行建模即可预测第t个数据，这样的话就可以使用如MLP（多层感知机模型）来训练

方案2：潜变量模型

引入潜变量$h_t$来表示过去信息$h_t = f(x_1,...,x_{t-1})$,则xt可以写作$x_t=p(x_t\mid h_t)$

$h_t=p(h_t\mid h_{t-1},x_{t-1})$

$x_t=p(x_t\mid h_t,x_{t-1})$

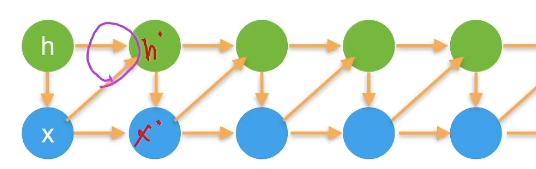
2、RNN循环神经网络

RNN是具有很强时序性的模型

RNN是一个隐变量模型，下述操作等价于一个全连接层

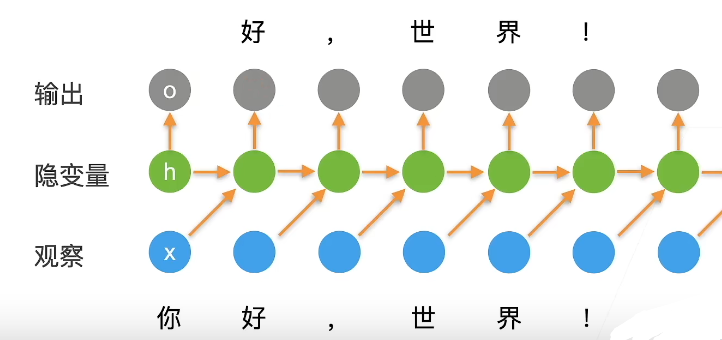
更新隐藏状态：

$h_t=\phi(W_{hh}h_{t-1}+W_{hx}x_t+b_t)$

输出：

$o_t=\phi(W_{ho}h_t+b_o)$

2.1 困惑度

衡量一个语言模型德好坏可以用平均交叉熵

$\pi=\frac{1}{n}\sum_{i=1}^n-logp(x_t\mid x_{t-1},...)$

p是语言模型的预测概率，$x_t$是真实值

NLP一般使用困惑度$exp(\pi)$（拉伸一下）来衡量，是为了平均每次可能选项：1是最好，无穷大是最差

2.2 梯度裁剪（？）

迭代中计算T个时间步上的梯度，在反向转播过程中产生长度为O（T）的矩阵乘法链，导致数值不稳定

梯度裁剪能有效预防梯度爆炸：如果梯度长度超过$\theta$，那么把梯度拖回$\theta$

$g\leftarrow min(1,\frac{\theta}{\mid g\mid})g$

2.3 RNN应用

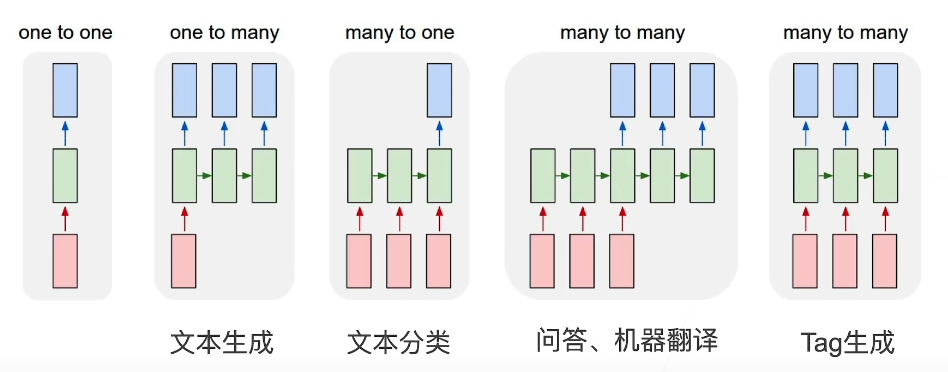
3、门控循环单元GRU

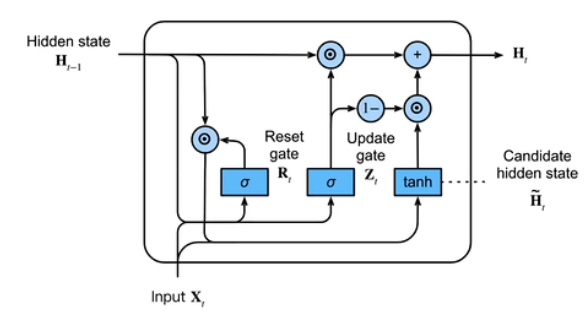
考虑到不是每个观察值都是同等重要的，所以想只记住相关的观察需要：

1. 能关注的机制（更新门update）
2. 能遗忘的机制（重置门reset）

3.1 门

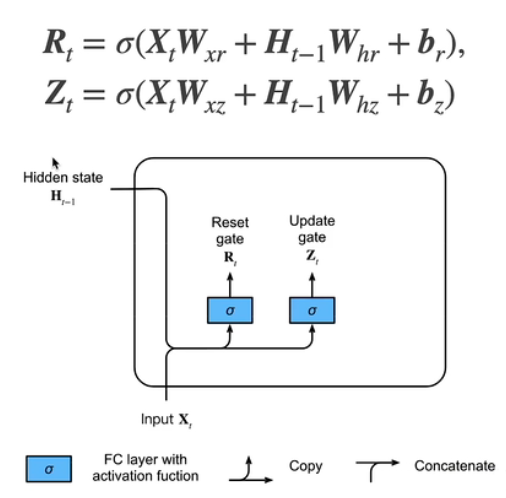
$R_t$：重置门

$Z_t$：更新门

$\sigma $：sigmoid激活函数操作（使Rt和Zt在（-1，1）之间）

和RNN相比，多出了两个可训练权重，同样是和全连接层等价

3.2 候选隐状态

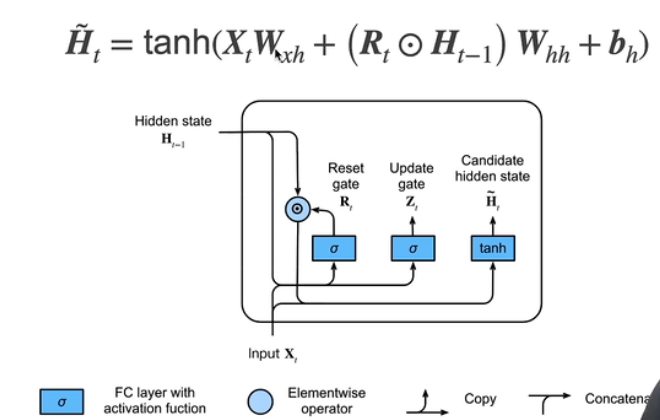
$R_t\circ H_{t-1}$表示按元素相点乘，如果Rt都是1则和RNN里的Ht计算相同，但是当Rt接近0时则表示遗忘之前隐变量里的信息

tanh（）双曲正切，激活函数的一种

3.3 隐状态

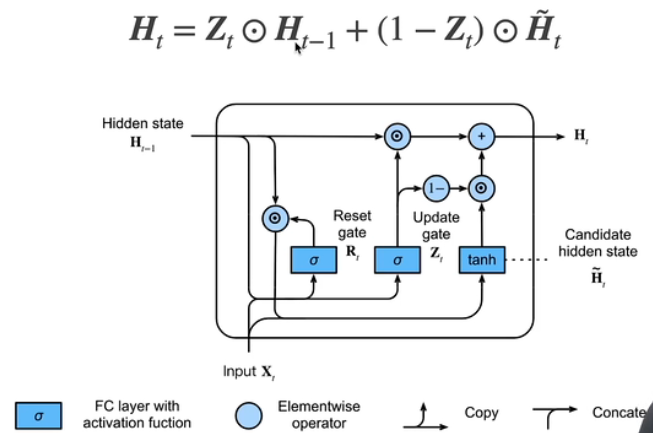
3.4 总结

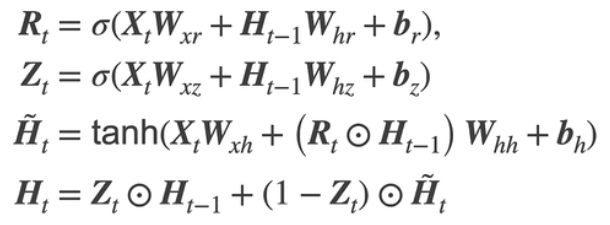
4、长短期记忆网络（LSTM）

思想和GRU差不多，试图权衡之前信息和当前信息的权重

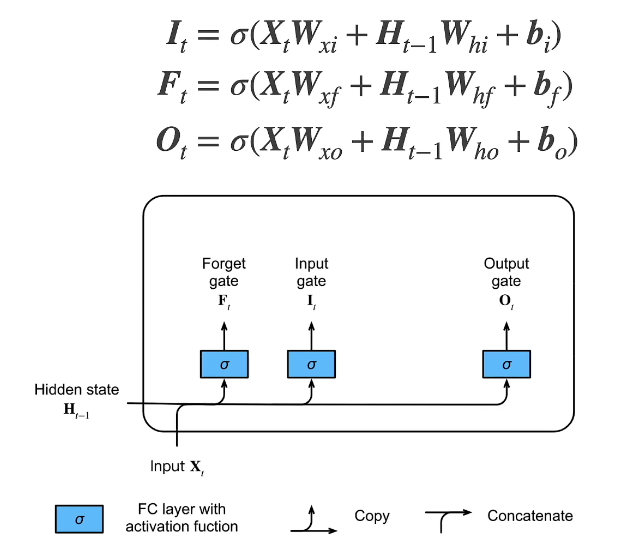
忘记门：将值朝0减少

输入门：决定是不是忽略掉输入数据

输出门：决定是不是使用隐状态

4.1 门

4.2 候选记忆单元

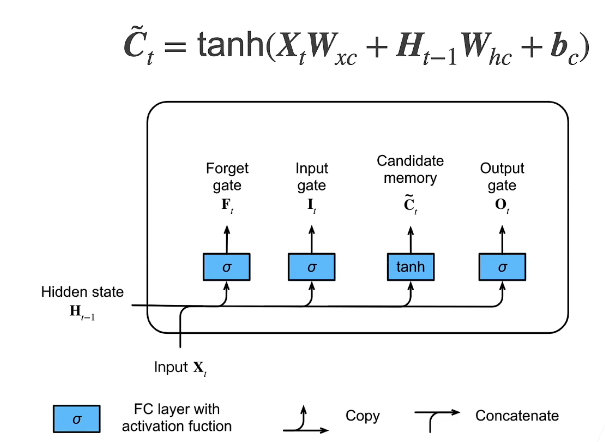
4.3 记忆单元

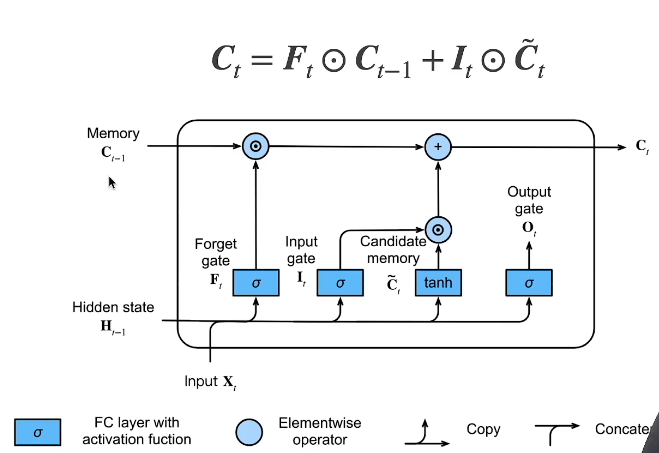
和GRU的隐状态计算类似，但是GRU的隐状态计算的两个权重是有关联的，这里记忆单元计算的两个权重是独立的。

因为这里的两个权重Ft和It是相互独立的，所以此时的Ct取值在（-2，2）之间

4.4 隐状态

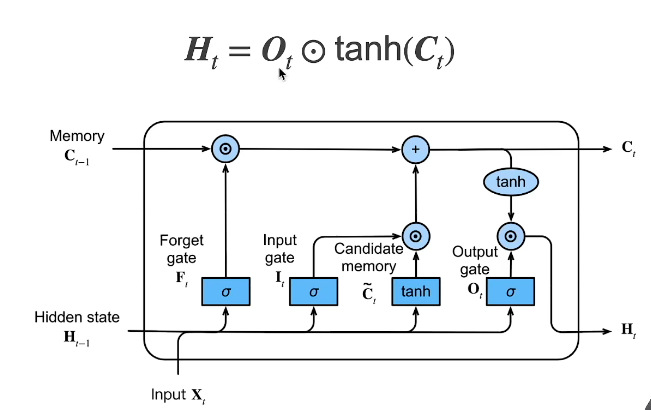
Ot是忘记门，控制Ht要不要输出，如果Ot等于1，就输出；如果Ot等于0，就不输出，之前的信息都不要了，等价于重置

4.5 总结

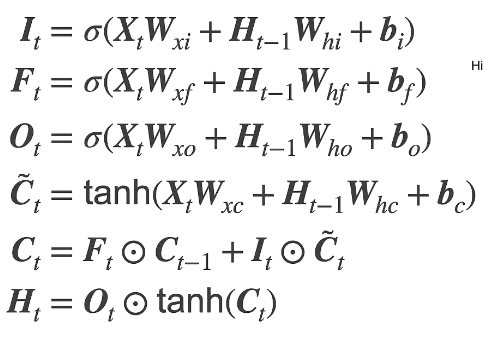
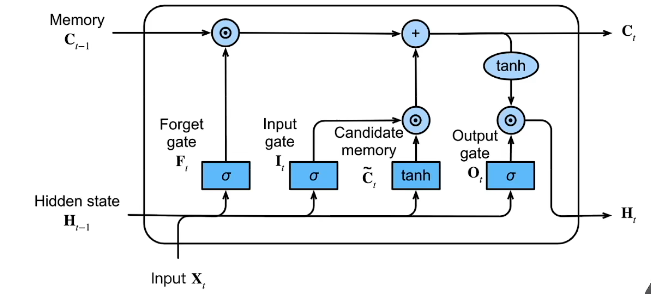
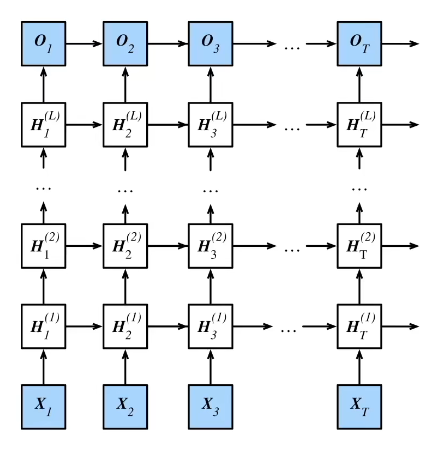
5、深层RNN

加深神经网络的目的是为了获得更多的非线性性，同理，RNN加深网络也是为了使隐藏状态获得更多的非线性性。

$h_t=\phi(W_{hh}h_{t-1}+W_{hx}x_t+b_t)$

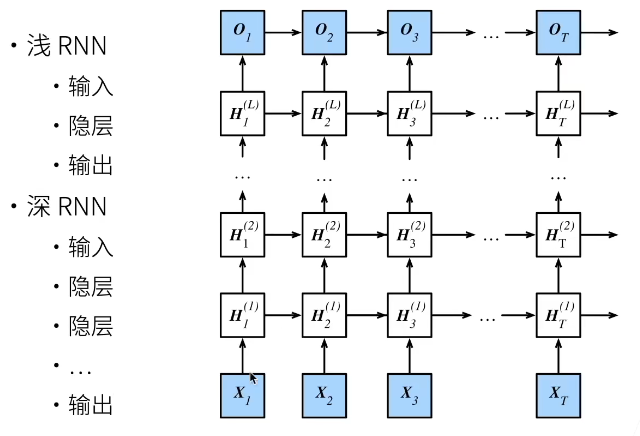
5.1 表达式

$H_t^1=f_1(H_{t-1}^1,X_t)$

$H_t^j=f_j(H_{t-1}^j,H_t^{j-1})$

$O_t=g(H_t^L)$

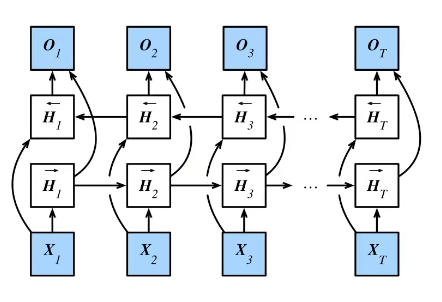
6、双向循环神经网络（pass）

思想是结合上下文来预测，结合过去和未来的信息来预测当前状态

不适合用来做推理（只知道之前的信息）

双向LSTM适合对语句进行特征提取（完形填空），对序列抽取特征

6.1 架构

一个前向RNN隐藏层：h1的隐藏状态信息给h2用

一个后向RNN隐藏层：h2的隐藏状态信息给h1用

合并两个隐状态得到输出

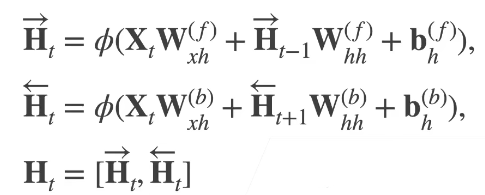
7、编码器-解码器架构（对CNN和RNN的一种理解）

编码器：将输入编程成**中间表达形式（特征）**便于机器学习

解码器：将中间表示解码成输出

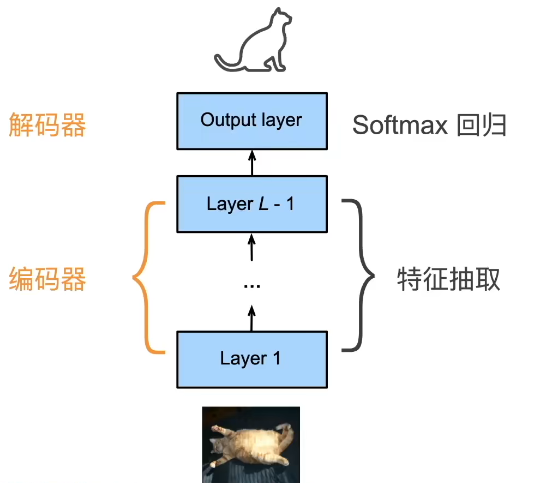
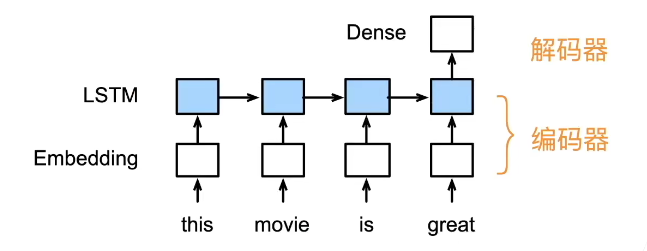
综上，一个模型可以被分成两块：

编码器处理输入，训练解码器

输入数据给解码器，生成输出

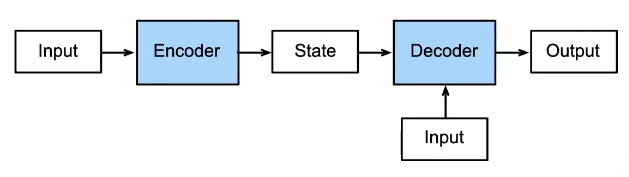
7.1 总结

在这个阶段，我们把以往的CNN模型以一种新的框架解释，在这种框架下，通过中间信息（特征）作为介质，接下来的模型可以实现不同长度的序列之间的转换。

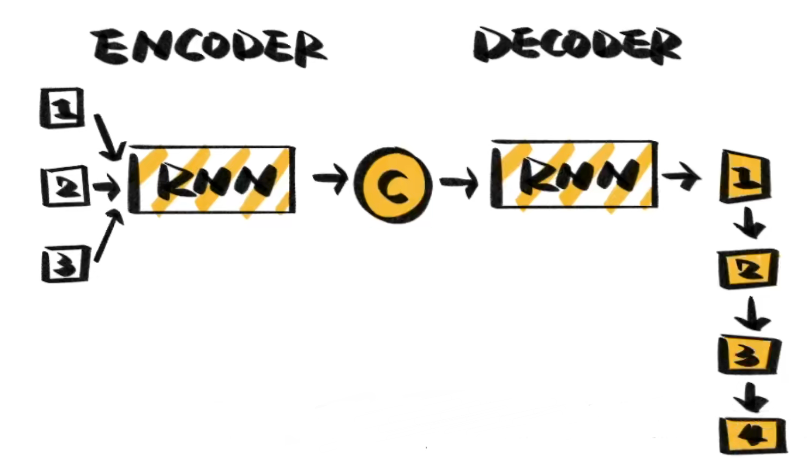
8、序列到序列学习（seq2seq）（pass）

用于解决复杂的神经语言程序学相关问题（？）

一开始用于机器翻译：给定一个源语言的句子，自动翻译成其他语言。

seq2seq就是一个编码器-解码器的架构

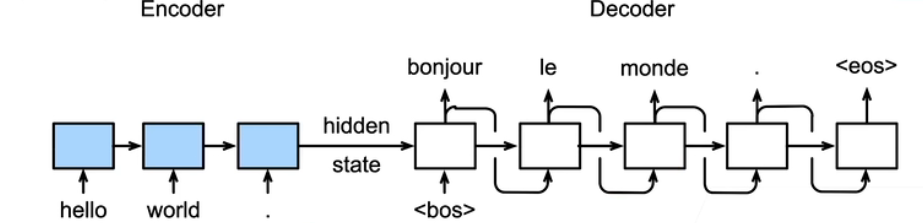
编码器是一个RNN，读取输入句子（可双向）（双向RNN可以做encoder，但不能做decoder）

解码器使用另外一个RNN输出

9、束搜索（？）（pass）

10、注意力机制

动物需要在复杂环境下有效关注值得注意的点（聚焦的感觉）

人类根据随意线索和不随意线索选择注意点

之前的卷积、全连接、池化都只考虑不随意线索

注意力机制则显式的考虑随意线索（随意：自主性提示，即想要干什么，其他的背景之类的是不随意）：

1. 随意线索被称之为查询（query）
2. 每个输入是一个值（value）和不随意线索（key）的对
3. 通过注意力池化层来有偏向性的选择某些输入

10.1 非参注意力池化层

1. 给定数据$(x_i,y_i),i=1,..,n$ （x是key，y是value）

2. 平均池化是最简单的方案：$f(x)=\frac{1}{n}\sum_iy_i$ （即不管x，直接把value做均值）

3. 更好的方案是60年代提出的Nadaraya-Watson核回归：

   ​ K（）是一个核函数，这里用来衡量x和xi之间的距离。大意是选取距离输入x更近的key的 value加权平均。（类似KNN）

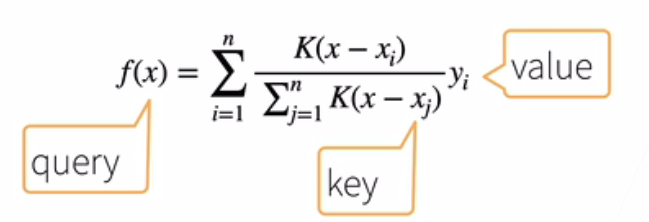
10.1.1 Nadaraya-Watson核回归

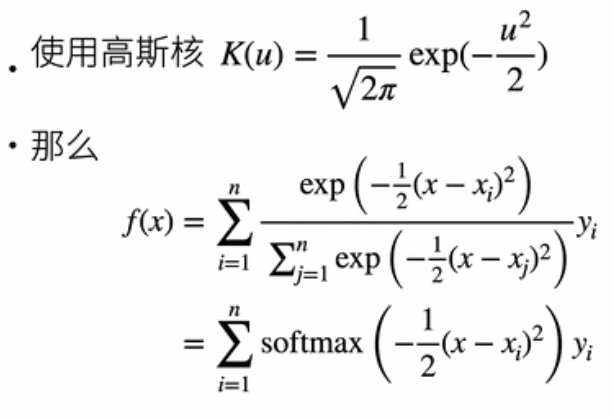
10.2 参数化的注意力机制

在Nadaraya-Watson核回归使用高斯核的基础上引入可以学习的参数w

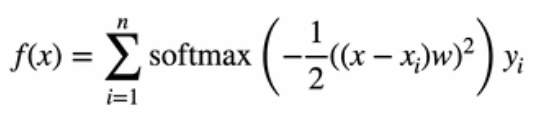
10.3 注意力分数

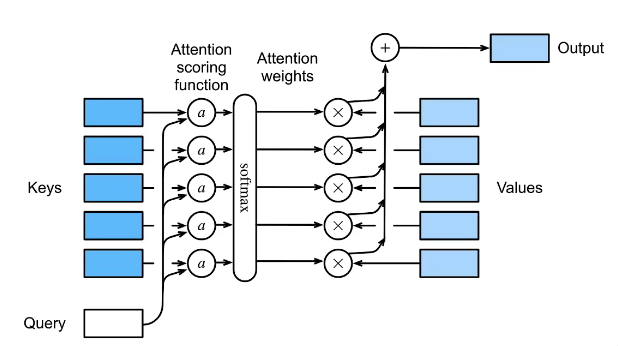
10.4 拓展到高纬度

假设query是一个长为q的向量 $q\in R^q$,m对key-value$(k_1,v_1)$,…,（k1是一个长为k的向量，v1是一个长为v的向量）这里$k_i\in R^k,v_i\in R^v$

注意力池化层表示为：（这里的a（）是注意力分数函数）

关于a（）的设计有以下两种思路

10.4.1 可加性注意力（Additive Attention）

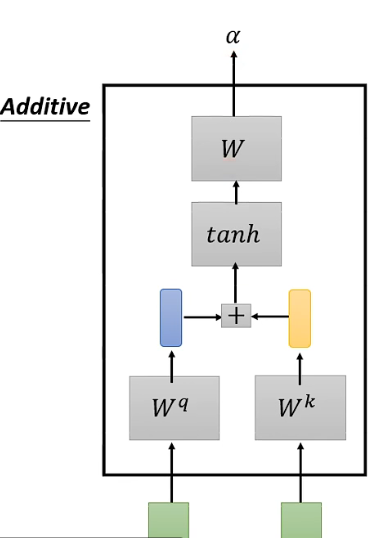
可学参数：

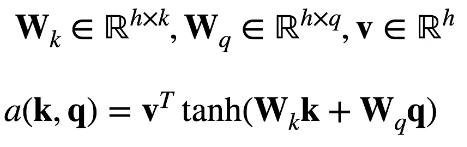
等价于将key和value合并（长为k的向量和长为q的向量合并）起来后放入到一个隐藏大小为h输出大小为1的单隐藏层MLP

10.4.2 Scaled Dot-Product Attention

Dot-product是最常用的方法（用在transformer中的）

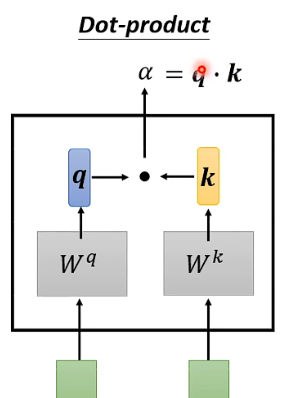
如果query和key都是同样的长度$q,k_i\in R^d$，那么可以让q和ki做内积除以根号d

处理根号d是为了使模型对向量长度不敏感

这里的处理相当于不学习参数

$a(q,k_i)=<q,k_i>/\sqrt{d}$

矩阵化（向量化）的版本：

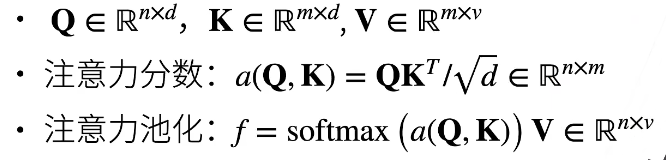
10.5 总结

注意力分数使query和key的相似度（距离的远近），注意力权重使分数的softmax结果

11、自注意力（？）

给定序列$x_1,...,x_n,\forall x_i\in R^d$

自注意力池化层将xi当做key、value、query来对序列抽取特征得到$y_1,...,y_n$，这里

$y_i=f(x_i,(x_1,x_1),...,(x_n,x_n))\in R^d$

每个输出都是考虑到了整个输入的序列信息

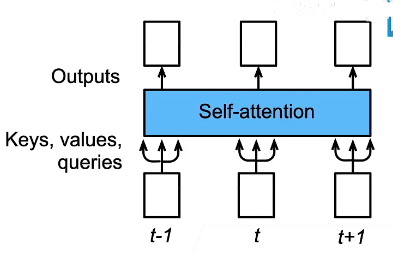
11.1 位置编码（？）

自注意力中输入的序列本身没有位置信息（即可以看作序列的每个数据是不分先后，没有差别的）

所以当需要位置信息时，则需要位置编码

（尚待研究）

11.2 关于图像的方法

使用自注意力机制处理图像的方法（图像可以被看作是一个向量）：

Self-attention GAN

DEtection Transformer（DETR）

11.3 自注意力与CNN

可以把CNN看作简化版的自注意力，因为CNN只关注卷积核范围内的信息，而自注意力是关注全图信息。

换个说法是自注意力可以通过学习来确定处理信息的范围（视野），而不是CNN那样人工确定。

当参数设定合适时，自注意力可以达到和CNN一样的效果。

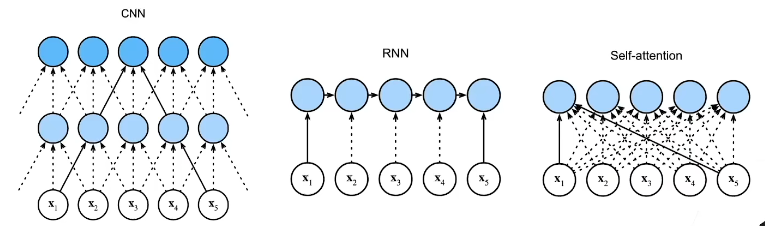
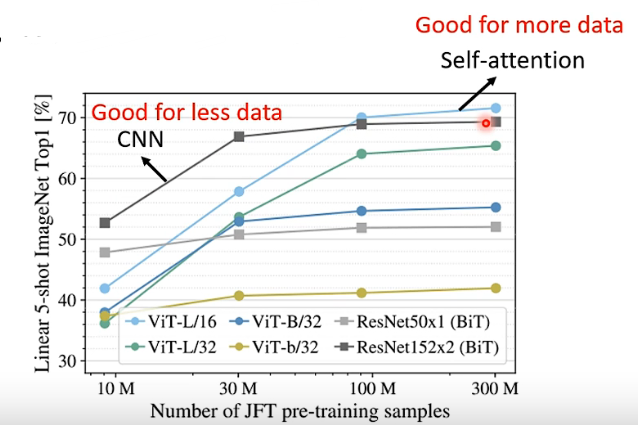
RNN的信息传递太长了，自注意力可以并行处理。

RNN与自注意力相比，已经过时了。

12、 Transformer（？）

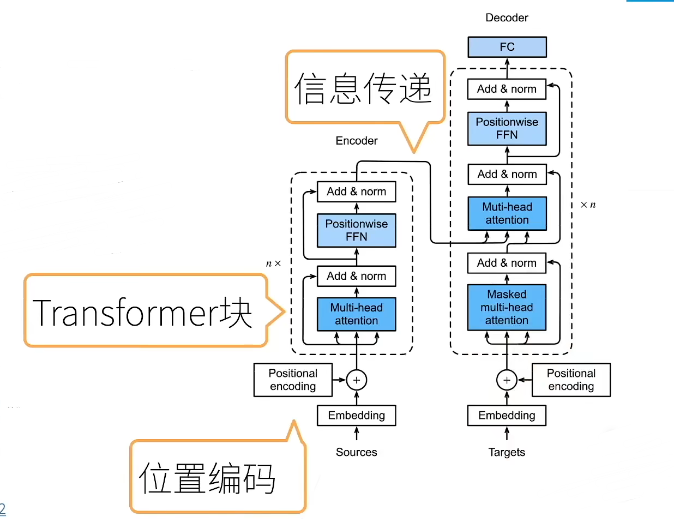
基于编码器-解码器架构来处理序列对

Transformer是纯基于注意力的架构

12.1 多头注意力

对同一key、value、query，希望抽取不同的信息：比如短距离关系和长距离关系

多头注意力使用h个独立的注意力池化：合并各个头（head）输出得到最终输出

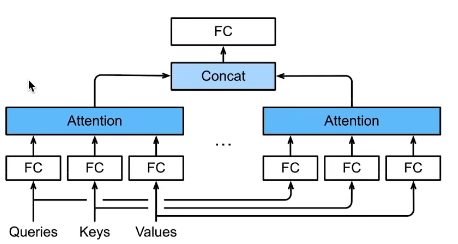
12.2 有掩码的多头注意力

解码器对序列中一个元素输出时，不应该考虑该元素之后的元素

所以需要通过掩码来实现：即计算$x_i$输出时，设当前序列长度为i

12.3 基于位置的前馈网络(Positionwise FNN)

一种全连接层

将输入形状由(b,n,d)变为(bn,d) （？）

12.4 总结

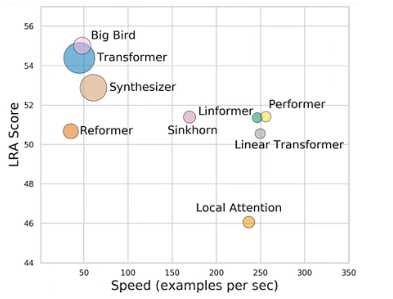
更多transformer变形见：

(强推)李宏毅2021/2022春机器学习课程_哔哩哔哩_bilibili

13、 生成式对抗网络GAN

14、 自监督式学习BERT

15、 自编码器

16、 神经网络压缩

17、 元学习Meta Learning

补充概念

end-to-end（端到端）:通过缩减人工预处理和后续处理，尽可能使模型从原始输入到最终输出，给模型更多可以根据数据自动调节的空间，增加模型的整体契合度。

数据集

Mnist

Iris

ImageNet（2010）